摘要： 在过去的几十年里，开发更强大的神经网络架构，并同时设计能够有效训练这些架构的优化算法，一直是提升机器学习模型能力的研究核心。尽管近年来取得了显著进展，尤其是在语言模型的发展方面，关于这类模型如何持续地学习/记忆、实现自我改进，并找到“有效解”等问题，依然存在根本性的挑战与未解之谜。本文提出一种新的学习范式 Nested Learning，它将一个模型一致地表示为一组嵌套的、多层级的和/或并行的优化问题，每个问题都拥有其自身的 “context flow”。NL 揭示了现有深度学习方法是如何通过压缩其自身的 context flow 来从数据中学习，并解释了 in-context learning在大模型中如何涌现。NL 进一步指出了一条路径，即通过引入更多“层级”来设计更具表达力的学习算法，从而获得更高阶的 in-context learning 能力。除了在神经科学上具有合理性、在数学上具备白盒特性之外，我们通过三项核心贡献来强调 NL 的重要性：1. Deep Optimizers：基于 NL，我们表明，广为人知的基于梯度的优化器（如 Adam、SGD with Momentum 等）其实是以梯度下降对梯度进行压缩的关联记忆模块。基于这一洞见，我们提出了一组更具表达力的优化器，具备更深的记忆和/或更强的学习规则；2. Self-Modifying Titans：利用 NL 对学习算法的洞见，我们提出一种新型序列模型，它通过学习自身的更新算法来学习如何修改自己；3. Continuum Memory System：我们提出一种新的记忆系统表述，推广了传统关于“long-term/short-term memory”的观点。将我们的自修改序列模型与该连续体记忆系统结合，我们提出一个名为 HOPE 的学习模块，并在语言建模、持续学习以及长上下文推理任务上展现出有前景的结果。

1. Intro

Deep Learning中堆叠多层网络带来了更大的容量、更强的复杂表征能力，更多的#FLOPs。“更深”的网络不一定能在多个方面提升模型的表达能力，如：

模型的“计算深度”不一定随着层数增加，其中很多层数在训练过程中可能会“消失”/被bypass，导致它相比于更简单的模型并不能改善表达能力；
某些参数类别的容量在加深/加宽中出现边际效益递减的情况；
由于超参数、优化器等各种问题，训练可能熟练到次优解；
模型的持续学习、新任务的快速适应能力、OOD数据的泛化能力等不会随着模型的简单堆叠而改善¹

为了克服以上挑战、解决问题，当前的工作主要集中在：

发展更有表达力的神经网络架构；
提出更贴合任务的目标函数；
设计更有效的优化算法；
在架构、目标、优化算法合适的前提下，在规模上进行scaling以增强表达性。

这样的研究方案塑造了Scaling Law，奠定了当前LLM的研究基础。LLM的发展是Deep Learning的一个重要里程碑，使得研究范式从面相特定任务的特定模型，转向了更通用的系统，并由此涌现出了多种能力。

然而，LLM在部署后，大体上仍然是“静止”的：它们能很好地执行在pre-training/post-training中学到的任务，但很难在即时上下文中获得新的能力。在这个方面，LLM唯一的能力是它在in-context learning中的能力，能够进行zero-shot/few-shot的任务。但是这个能力实际上仍然是显然不足的，并且近期尝试克服此问题的方案，要么计算代价高昂、要么依赖外部组件（本质上还是在scaling而不是获取新能力）、要么泛化能力不足，或者严重🫡灾难性遗忘的影响。

这促使研究者重新思考：是否需要重新设计 机器学习模型，以及是否需要一种超越“堆层”的新学习范式，以在持续学习 情境中真正释放 LLMs 的潜力。 当前模型只“经历”即时当下。 为更好地说明 LLM 的静态性，我们借用** 顺行性遗忘（anterograde amnesia）** 的类比——这是一种神经学状况：自发病起，个体无法再形成新的长期记忆，而既有记忆依旧完好。这种状况将个体的知识与体验限制在** 短窗口的现在与发病之前的久远过去**，于是当下不断被体验成“新的”。当前 LLM 的记忆处理系统存在类似的模式：它们的知识要么局限于** 可装入其 context window 的即时上下文**，要么来自 ** MLP 层中存储的 久远过去**（即在“** end of pre-training**”之前）。这一类比促使我们转向** 神经生理学文献，考察大脑如何 巩固短期记忆**。

1.1. Human Brain Perspective and Neurophysiological Motivatgion

人脑在做continual learning的时候十分高效，一般归结于其“神经可塑性（neuroplasticity）”。近期研究支持长期记忆的形成至少设计两种相互补充的巩固过程：

在线巩固（突触巩固），在学习时立刻/很快开始发生；此时，新的、起初脆弱的记忆痕迹得以稳定，并开始从短期转移到长期存储；
离线巩固（系统巩固），在海马体的 sharp-wave ripples（SWRs，尖波-涟漪）期间反复重放近期编码的模式，并与皮层睡眠纺锤波与慢振荡协调，从而加强与重组记忆，并支持其向皮层部位的转移

回到顺行性遗忘的类比，证据显示该状况会影响这两个阶段，尤其是“在线”巩固，主要因为海马体是新陈述性记忆编码的入口，其受损意味着新信息永远无法写入长期记忆。正如上文所述，LLMs——更具体地说，基于 Transformer 的骨干——在 pre-training 结束后呈现出类似情形：上下文中的信息无法影响长期记忆参数²（如前馈层），因此模型无法获得新的知识或技能，除非这些信息仍然保存在短期记忆（如注意力/attention）之中。为此，尽管第二阶段在记忆巩固中同样（或更）关键，其缺失也会破坏过程并可能导致记忆丢失，本文聚焦第一阶段：将记忆巩固视作在线过程。

Notations

输入： $x \in R^{N \times d_{in}}$ ， $M_{t}$ 表示模型在 $t$ 时刻的记忆； $K, V, Q$ ； $k_{t}, v_{t}, q_{t}$ 是对应的列向量； $p (f)$ 是 $f$ 的分布，采用带残差连接的简单MLP作为记忆模块 $M (\cdot)$ ； $θ_{M} \supseteq {W_{1}, W_{2}, ..., W_{L_{M}}}$ 是参数； $W^{(l)}$ 中上标圆括号是不同的层级的参数。

2. Nested Learning

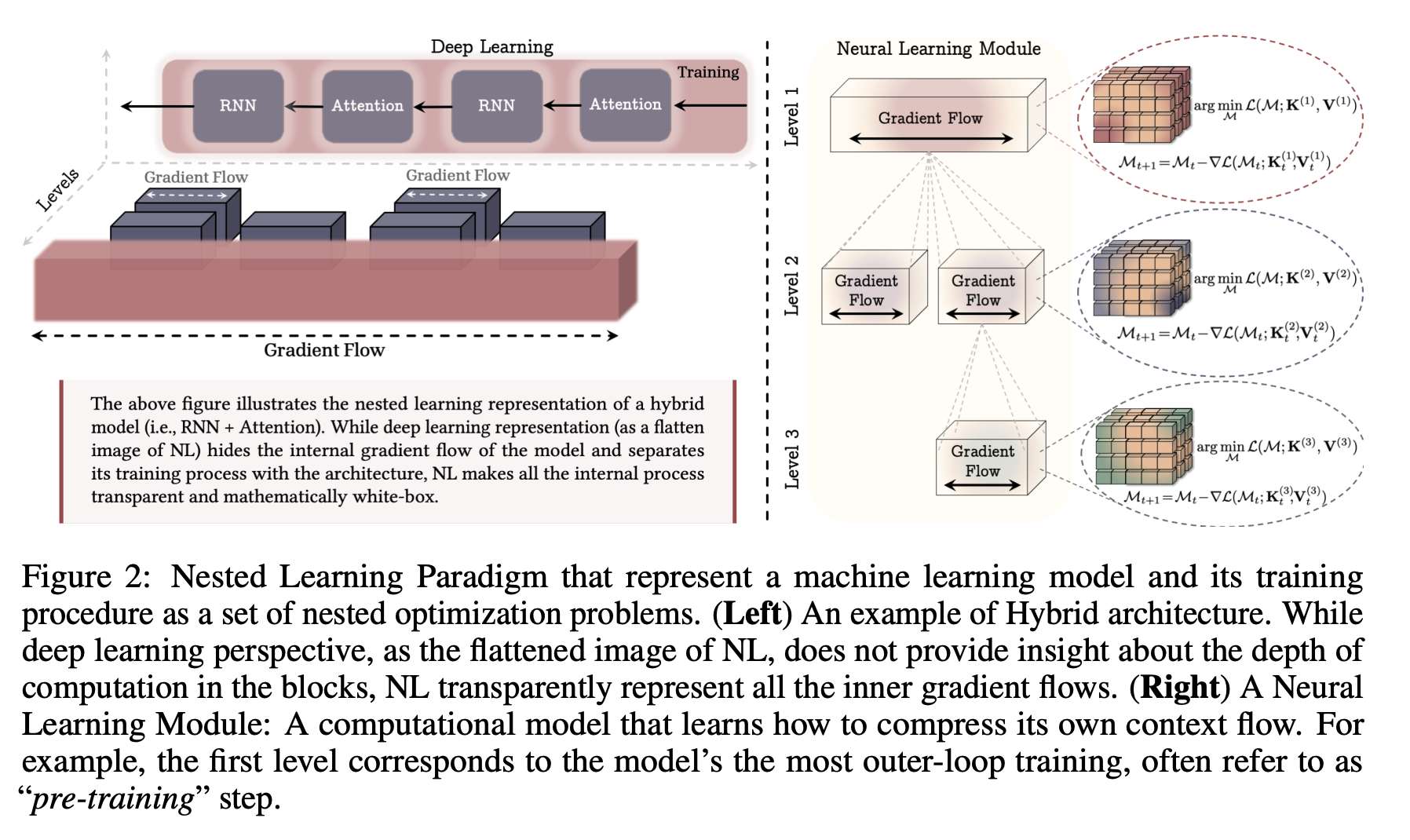
2.1. Associative Memory

Associative memory ——即在事件之间形成并提取连接的能力——是一种基本的心理过程，也是人类学习不可分割的组成部分。

给出以下记忆与学习的定义：

Learning vs. Memorization:
Memory is a neural update caused by an input, and learning is the process for acquiring effective and useful memory.

本文认为，所有的“Cmoputational Sequence Model”（包括优化器+网络本身）都是压缩自身context flow的associative memory system。

定义Associative Memory： 给定 $K \subseteq R^{d_{k}}$ 与 $V \subseteq R^{d_{v}}$ ，associative memory是一个算子 $M : K \to V$ ，用来在两者间建立映射。为了学习此映射，引入目标函数 $\hat{L} (\cdot; \cdot)$ 来度量映射的质量。 $M$ 可以定义为：

M^{*} = ar g M min \tilde{L} (M (K); V)

算子本身就是一种记忆，而优化过程就是学习过程。

A Simple Example of MLP Training

考虑在任务 $τ$ 、数据集 $D_{train} = {x_{1}, ..., x_{∣ D_{train} ∣}}$ ，优化目标 $L (\cdot; \cdot)$ ，优化问题：

W^{*} = ar g W min L (W; D_{train}),

梯度下降的更新：

W_{t + 1} = W_{t} - η_{t + 1} \nabla_{W_{t}} L (W_{t}; x_{t + 1}) = W_{t} - η_{t + 1} \nabla_{y_{t + 1}} L (W_{t}; x_{t + 1}) \otimes x_{t + 1}, where x_{t + 1} \sim D_{train},

令 $u_{t + 1} = \nabla_{y_{y + 1}} L (W_{t}; x_{t + 1})$ ，反向传播过程就是一个寻找最优的associative memory，将 $D_{train} = {x_{t}}_{t = 1}^{∣ D_{train} ∣}$ 映射到对应的 $u_{t + 1} = \nabla_{y_{y + 1}} L (W_{t}; x_{t + 1})$ 。也就是说，令 $M (\cdot) = W_{t}$ ，参数化了记忆，点积相似度衡量映射质量，可以写得：

W_{t + 1} = ar g W min ⟨ W x_{t + 1}, u_{t + 1} ⟩ + \frac{1}{2 η _{t + 1}} ∥ W - W_{t} ∥_{2}^{2} = ar g W min ⟨ W x_{t}, \nabla_{y_{t + 1}} L (W_{t}; x_{t + 1}) ⟩ + \frac{1}{2 η _{t + 1}} ∥ W - W_{t} ∥_{2}^{2}

$u_{t + 1} = \nabla_{y_{y + 1}} L (W_{t}; x_{t + 1})$ 在上面的公式中类似一种局部的“惊讶信号”，刻画了当前输出与目标所施加结构的不匹配程度。

因此，这一路径把训练阶段 翻译为：获取一种有效记忆 ，把数据样本映射到其在表征空间的 LSS （由目标函数施加的结构约束所定义的不匹配）。

进一步地，引入带动量的变体：

W_{t + 1} = W_{t} - m_{t + 1}, m_{t + 1} = m_{t} - η_{t + 1} \nabla_{W_{t}} L (W_{t}; x_{t + 1}) = m_{t} - η_{t + 1} \nabla_{y_{t + 1}} L (W_{t}; x_{t + 1}) \otimes x_{t + 1} .

注意到 $\nabla_{W_{t}} L (W_{t}; x_{t + 1})$ 与递推无关，可以预先计算。令 $u_{t + 1} = \nabla_{W_{t}} L (W_{t}; x_{t + 1})$ ，可以进一步：

W_{t + 1} m_{t + 1} = W_{t} - m_{t + 1} = ar g m min - ⟨ m, \nabla_{W_{t}} L (W_{t}; x_{t + 1}) ⟩ + η_{t + 1} ∥ m - m_{t} ∥_{2}^{2} = ar g m min - ⟨ m x_{t + 1}, \nabla_{y_{t + 1}} L (W_{t}; x_{t + 1}) ⟩ + η_{t + 1} ∥ m - m_{t} ∥_{2}^{2}

优化问题变为一个带自适应学习率 $η_{t + 1}$ 的梯度下降过程。动量项可以解释为：

一个无key的associative memory，将梯度压缩到它的参数中，或是
一个学习将数据点映射到对应的LSS-Value上的associative memory。

可以看到带动量的训练本身形成量两层优化过程，即又有优化自己本身的记忆，还有“优化优化记忆的过程”（即调整动量/自适应学习率）的优化过程。

归纳上述的描述，我们在训练一个MLP的过程中：

纯梯度下降是单层的associative memory；学习把数据点映射到LSS值；
带动量的梯度下降时两层associative memory；内层学习把梯度存入其参数，外层使用内层记忆更新slow weight $W_{t}$ 。

尽管这些在架构与优化器层面都是最简单的例子，但我们可以进一步追问：在更复杂的设定下，是否仍能得到相似结论？

An Example of Architectural Decomposition

将MLP换成Linear Attention，更复杂的例子。回顾一下Linear Attention：

k_{t} = x_{t} W_{k}, v_{t} = x_{t} W_{v}, q_{t} = x_{t} W_{q} M_{t} = M_{t - 1} + v_{t} k_{t}^{⊤} y_{t} = M_{t} q_{t}

$M_{t}$ 也可以理解为一个associative memory $M_{t} (\cdot)$ 的优化过程，目标是将key和value的映射压缩到参数中。更具体地，若令 $\hat{L} (M_{t - 1}; k_{t}, v_{t}) := - ⟨ M_{t - 1} k_{t}, v_{t} ⟩$ ，并用梯度下降优化该记忆，设 $η_{t} = 1, \nabla \hat{L} (M_{t - 1}; k_{t}, v_{t})$ ，则记忆更新的过程为：

M_{t + 1} \Rightarrow M_{t + 1} = ar g M min ⟨ M k_{t + 1}, v_{t + 1} ⟩ + ∥ M - M_{t} ∥_{2}^{2} with gradient descent, = M_{t} - \nabla \tilde{L} (M_{t}; k_{t + 1}, v_{t + 1}) = M_{t} + v_{t + 1} k_{t + 1}^{⊤},

和上面的式子形式相同，可以看到Linear Attention本身的memory就也可以看作是一种associative memory更新的过程。

2.2. Nested Optimization Problems

受脑电节律层级启发——不同脑区的信息处理具有不同频率——我们用各个优化问题的更新速率来在多层级中为组件排序。为此，我们令“对单个数据点的一次更新”为时间单位，从而提出：

定义2 Update Frequency ：对于任意组件 $A$ （不管是带参数weight/动量，的还是非参数化的如attention block），定义单位时间内该组件的更新次数为它的频率 $f_{A}$ 。

拥有频率后可以进一步定义偏序关系 $(\cdot ≻ \cdot)$ ， $A ≻ B$ 表示 $f_{A} \geq f_{B}$ ，但若 $f_{A} = f_{B}$ 时，时刻 $t$ 计算 $B$ 的状态需要计算 $A$ 的状态，则 $A ⊁ B, B ⊁ A$ ，记作 $A = B$ 。

据此操作，可以将组件分入一个有序层级集合中：

同一层内的组件具有相同的更新频率；
层级越高，更新频率越低。

基于上述嵌套学习问题的定义，我们将 Neural Learning Module 定义为一种新的模型表征方式：它把一个机器学习模型表示为由相互连接的组件构成的系统，且每个组件都有其独立的梯度流。需要强调的是，这与 deep learning 是正交的：nested learning 允许我们定义层级更多的神经学习模型，从而得到更具表达力的架构。 Nested learning allows computational models that are composed of multiple (multi-layer) levels to learn from and process data with different levels of abstractino and time-scales.

2.3. Optimizers as Learning Modules

回顾带动量的梯度下降：

W_{i + 1} m_{i + 1} = W_{i} + m_{i + 1} = α_{i + 1} m_{i} - η_{t} \nabla L (W_{i}; x_{i})

其中 $m_{i}$ 时状态 $i$ 下的动量， $α_{i}, η_{i}$ 分别是自适应的学习率和动量。令 $α_{i + 1} = 1$ 的假设下，动量项是

m min ⟨ m \nabla L (W_{i}; x_{i})^{⊤}, I ⟩ .

的梯度下降的优化结果，即动量本身是一个meta memory，学习如何将目标函数的梯度记忆到自己的参数重。

Extention: More Expressive Association

考虑到动量是一个没有value相关的associative memory，一个直观的提升其表达能力的方法是让value参数 $v_{i} = P_{i}$ ，动量进一步变成最小化

m min ⟨ m \nabla L (W_{i}; x_{i})^{⊤}, P_{i} ⟩,

的问题。梯度下降的视角下更新写作：

W_{i + 1} = W_{i} + m_{i + 1} m_{i + 1} = α_{i + 1} m_{i} - η_{t} P_{i} \nabla L (W_{i}; x_{i}) .

等价于在momentum GD中引入了preconditioning。

实际上，预条件化意味着：动量项是一个关联记忆，学习如何将 $P_{i}$ 和 $\nabla L (W_{i}; x_{i})$ 之间的映射压缩到其参数中。哪怕使用“合理”的（例如 random features）预条件化，也能改进“原始版、无 value 的动量记忆”（即把所有梯度映射到同一个 value）的表达性；而上述视角进一步提示：什么样的预条件化更有用——动量作为记忆要把梯度映射到相应的values，因此“梯度的函数”（例如包含 Hessian 信息）能为记忆提供更有意义的映射。

Extention: More Expressive Objectives

点积相似度可能不够好，一个自然的修改是改用L2 Loss优化 $m \nabla L (W_{i}; x_{i})^{⊤} - P_{i}_{2}^{2}$ ：

W_{i + 1} = W_{i} + m_{i + 1} m_{i + 1} = (α_{i + 1} I - \nabla L (W_{i}; x_{i})^{⊤} \nabla L (W_{i}; x_{i})) m_{i} - η_{t} P_{i} \nabla L (W_{i}; x_{i}),

这个更新由Hebbian规则变成Delta-Rule，更有效管理动量记忆的优先容量。

Extention: More Expressive Memory

将一个memory换成MLP等，可以扩展：

W_{i + 1} = W_{i} + m_{i + 1} (u_{i}), m_{i + 1} = α_{i + 1} m_{i} - η_{t} \nabla L^{(2)} (m_{i}; u_{i}, I),

其中 $u_{i} = \nabla L (W_{i}; x_{i})$ ， $\nabla L^{(2)} (\cdot)$ 是动量的内层目标，这个变体称为Deep Momentum Gradient Descent。

Extention: None Linear Outputs

进一步在动量记忆上叠加非线性，即

W_{i + 1} = W_{i} + σ (m_{i + 1} (u_{i})), m_{i + 1} = α_{i + 1} m_{i} - η_{t} \nabla L^{(2)} (m_{i}; u_{i}, I),

如果取 $σ (\cdot) = Newton-Schulz (\cdot)$ ，就变成Muon优化器。

Going Beyond Simple Backpropagation

W_{t + 1} = W_{t} - η_{t + 1} \nabla_{W_{t}} L (W_{t}; x_{t}) = W_{t} - η_{t + 1} \nabla_{y_{t}} L (W_{t}; x_{t}) \otimes x_{t}, where x_{t} \sim D_{train}

从关联记忆的角度，等于对

W min ⟨ W x_{t}, \nabla_{y_{t}} L (W_{t}; x_{t}) ⟩ .

做一步梯度下降，但是相当于没有考虑到 $x_{t}$ 和其他样本之间的关系，可以改写为：

W min ∥ W x_{t} - \nabla_{y_{t}} L (W_{t}; x_{t}) ∥_{2}^{2}

对应的梯度下降：

W_{t + 1} = W_{t} (I - x_{t} x_{t}^{⊤}) - η_{t + 1} \nabla_{W_{t}} L (W_{t}; x_{t}) = W_{t} (I - x_{t} x_{t}^{⊤}) - η_{t + 1} \nabla_{y_{t}} L (W_{t}; x_{t}) \otimes x_{t}, where x_{t} \sim D_{train},

后文提出的HOPE架构就使用这个方法作为对应的内部优化器。

3. HOPE: A Self-Referential Learning Module with Continuum Memory

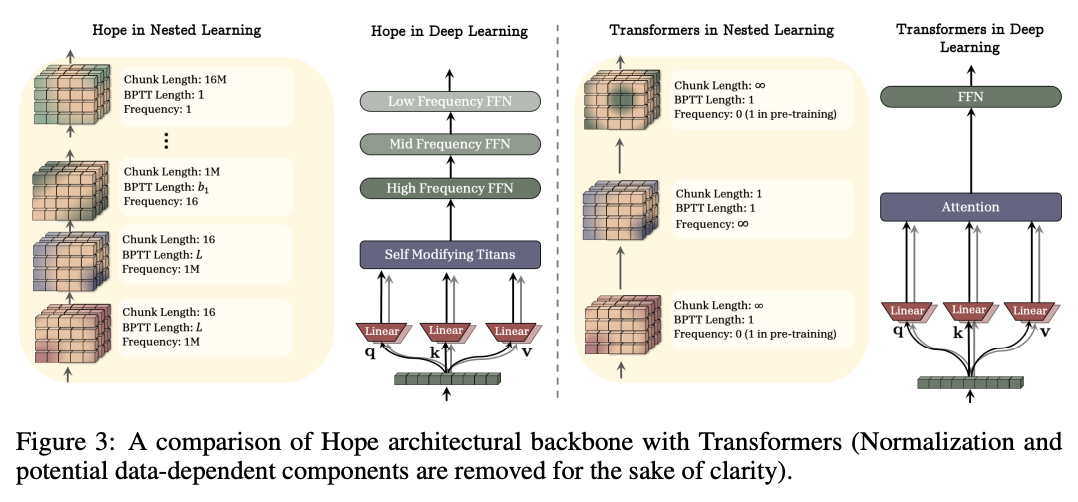
正文内容全在附录里，问题是Open Review上也看不到附录啊

4. Experiments

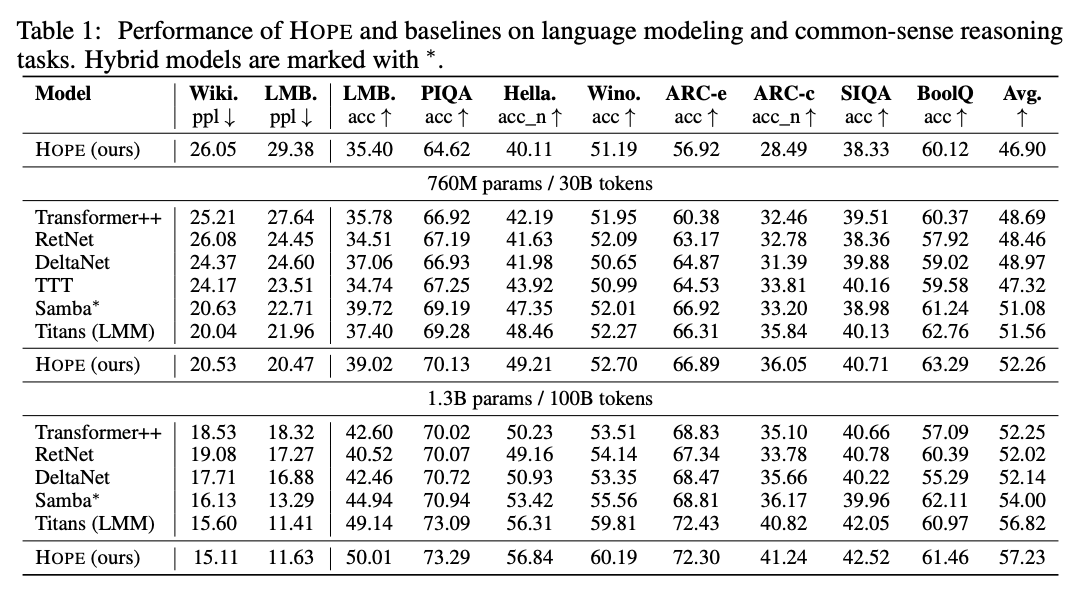
前面那些故事讲的太久了，但说实话真的没什么新的东西，内容在现在Linear Attention/Test Time Training社区里面讲过很久了。benchmark也没什么和Continual Learning相关的。

对吗？只考虑OOD的话似乎和现在的scale up的想法是相冲突的。 ↩
这个角度似乎也是Test Time Training/Linear Attention可以进行例证说明的部分，Fast Weight也是一种短期记忆。 ↩

Nested Learning: The Illusion of Deep Learning Architectures