Titans: Learning to Memorize at Test Time

原文：arXiv:2501.00663 · Behrouz et al., NeurIPS 2025

摘要： 在过去的十多年里，有关如何有效利用 RNN 和注意力机制的研究已经取得了广泛的进展。循环模型的目标是将数据压缩到一个固定大小的记忆（称为隐藏状态，hidden state）中，而注意力机制允许模型关注整个上下文窗口，从而捕获所有标记之间的直接依赖关系。然而，这种对依赖关系的更精确建模需要二次计算成本，这限制了模型只能处理固定长度的上下文。我们提出了一种新的神经长期记忆模块（neural long-term memory module），它学习记忆历史上下文，并在利用长时信息的同时帮助注意力机制专注于当前上下文。我们展示了这种神经记忆模块具有快速并行化训练的优势，同时还能保持快速推理能力。从记忆的角度看，我们认为，由于注意力机制的上下文有限但依赖关系建模精确，它更像是短期记忆；而神经记忆则因为能记忆数据，表现得更像一种长期、持久的记忆。基于这两个模块，我们引入了一种新的架构家族，称为 Titans，并提出了三种变体，旨在探讨如何有效地将记忆融入到这种架构中。我们的实验结果显示，在语言建模、常识推理、基因组学和时间序列任务中，Titans 比 Transformers 和最近的现代线性循环模型更加高效。此外，在 “大海捞针” 任务中，与基线相比，Titans 在超过 200 万的上下文窗口规模下表现出了更高的准确性，并且能够有效扩展。

“The true art of memory is the art of attention!” ——Samuel Johnson, 1787.

1. Introduction

Transformer 主要为人诟病的还是平方的复杂度，这对计算时间和显存开销都很致命。线性注意力这样的改进导致的掉点都比较大，因为他们往往将数据压缩到一个较小的矩阵状态，这会导致一种矛盾：

一方面，线性模型用于提升扩展性和效率（线性对比二次复杂度），在超长上下文中展现优势；另一方面，超长上下文无法被有效地压缩到一个小的向量或矩阵状态中。

作者觉得现在的架构还是不够精致，尤其是在记忆方面。作者认为最好是能有一些类似人脑的、复杂的长期、短期记忆，和上下文 Attention 这样的模块，让模型能够获得主动从数据中学习并且记忆过去历史的抽象能力。

Memory Perspective

从记忆的角度来看，RNN 拥有向量型的记忆，每次推理就是更新和检索；Transformer 的记忆就是 QK 对，每次 append 新的记忆，通过检查 V 和 K 的相似度检索记忆。这种结构的不同让我们提出下面的问题：

什么是好的记忆结构？
什么是好的记忆更新方式？
什么是好的记忆检索方式？
如何设计一个有效的架构，将不同的互联记忆模块整合在一起？
是否需要一个深度记忆模块，从而存储/记住久远的过去？

Contributions and Roadmap

Neural Memory，提出了一种深度神经长期记忆模块，能够在测试时学习如何将数据记忆到参数中，并且这种设计能够让 “违反预期” 的事件更加容易被记住。还提出了一种衰减机制，考虑记忆大小和数据惊讶程度的比例，并且证明这种衰减机制时现代 RNN 中遗忘机制的一个推广。有趣的是，这种机制等价于使用小 batch 训练一个 meta neural network。
Titans Architectures，提出了将上面这种记忆模块集成到深度学习模型中的架构，包含
- Core，包含短期记忆，数据处理的主要流程
- Long-term Memory，长期记忆
- Persistent Memory，可学习、数据无关的参数，编码任务相关的知识
Experimental Results，跑了一些 LLM 常见的小任务，尤其是上下文长度相关的 benchmark。

2. Preliminaries

令 $x \in \mathbb{R}^{N \times d_{\text{in}}}$ 为输入， $M$ 为神经网络（神经记忆模块）， $Q 、 K 、 V$ 分别表示注意力机制中的查询、键和值， $M$ 表示注意力掩码。在分段序列时，用 $S(i)$ 表示第 $i$ 个段。本文中，我们不严格区分符号，并使用下标表示矩阵、向量或段的特定元素。例如， $S(i)_j$ 表示第 $i$ 段的第 $j$ 个令牌。唯一的例外是带有 $t$ 的下标，专门用于索引时间上的递归或神经网络在时间 $t$ 的状态。给定神经网络 $N$ 和数据样本 x ，我们用 $N(x)$ （或 $N^*(x)$ ）表示有（或无）权重调整的前向传播。同样，我们用 $N(k)$ 表示神经网络的第 $k$ 层。

2.1. Backgrounds

Attention

Transformer 作为许多深度学习模型的事实标准骨干架构，基于注意力机制。给定输入 $x \in \mathbb{R}^{N \times d_{\text{in}}}$ ，因果注意力根据输入相关的键、值和查询矩阵通过 $softmax$ 计算输出 $y \in \mathbb{R}^{N \times d_{\text{in}}}$ ：

Q = xW_Q, \quad K = xW_K, \quad V = xW_V,

y_i = \frac{\sum_{j=1}^i \exp(Q_i^\top K_j / \sqrt{d_{\text{in}}}) V_j}{\sum_{\ell=1}^i \exp(Q_i^\top K_\ell / \sqrt{d_{\text{in}}})},

输出计算至少需要 $N \times d_{\text{in}}$ 的操作数，这导致长序列的内存消耗较大、吞吐量较低。

Efficient Attentions

研究主要集中在：

基于 IO 优化，如 flash attention
稀疏化注意力矩阵
softmax 的近似计算
核函数代替（线性注意力）

本文主要讨论线性注意力机制，用 $\phi(\cdot,\cdot)$ 代替 softmax，其中 $\phi(x, y) = \phi(x) \phi(y)$ ，有：

y_i = \frac{\phi(Q_i)^\top \sum_{j=1}^i \phi(K_j) V_j}{\phi(Q_i)^\top \sum_{\ell=1}^i \phi(K_\ell)}.

通过在每一步复用 $\sum_{j=1}^i \phi(K_j)$ 和 $\sum_{\ell=1}^i \phi(K_\ell)$ 提高了吞吐量。当核函数选择为单位矩阵时，上述公式还可以表示为递归形式：

M_t = M_{t-1} + K_t^\top V_t, \quad y_t = Q_t M_t,

Modern Linear Models and Their Memory Perspective

把 RNN 的隐藏层看成某种记忆，可以分为

M_t = f(M_{t-1}, x_t), \quad \text{(写操作)}

和

y_t = g(M_t, x_t), \quad \text{(读操作)}

其中 $f(\cdot, \cdot)$ 表示写函数， $g(\cdot, \cdot)$ 表示读函数。下标 $t$ 表示时间 $t$ 的记忆状态。从这一视角看，线性 Transformer 的递归公式等价于将键和值 $(K_t, V_t)$ 加性地压缩并写入矩阵值记忆单元 $M_t$ 。因此，在处理长上下文数据时，这种加性过程容易导致记忆溢出，严重影响模型性能。之前的的工作会：1. 添加遗忘机制；2. 改进写操作，比如删掉可能重复的记忆；

Memory Modules

像之前的 RNN，包括用一些 MLP 层，但是这种研究都不够复杂，也不是很深入。

3. Learning to Memorize at Test Time

3.1. Long-term Memory

记忆化在神经网络中通常被认为是一种不良现象，因为它限制了模型的泛化能力，引发隐私问题，并导致测试时性能不佳。此外，在测试时，数据可能是分布外的，训练数据的记忆化可能无助于模型的表现。我们提出，需要一个在线元模型来学习在测试时如何记忆和遗忘数据。在这一设置中，模型学习一个能够记忆的函数，但不对训练数据过拟合，从而在测试时表现出更好的泛化能力。

Learning Process and Surprise Metric

记忆的目标是将过去的信息 $x_1, ..., x_{t-1}$ 压缩到长期记忆模块 $M_t$ 的参数中。依照和过去不同的（违反直觉的，惊讶的）事件更容易被记住，可以给出一个直觉的惊讶度描述：

M_t = M_{t-1} - \theta_t \nabla \ell(M_{t-1}; x_t).

但是这种惊讶度可能会在一个较大的惊讶之后遗漏信息。梯度在几个令人惊讶的步骤后可能变得非常小，从而陷入平坦区域（即局部极小值），遗漏序列某些部分的信息。从人类记忆的角度看，一个事件可能不会长时间持续令人惊讶，但其初始惊讶足够强烈以吸引注意力，从而记住整个时间帧。

为了改进，将惊讶度分为过去惊讶和瞬时惊讶两个部分：

M_t = M_{t-1} + S_t,

S_t = \eta_t \underbrace{S_{t-1}}_{\text{Past Surprise}} - \theta_t \underbrace{\nabla \ell(M_{t-1}; x_t)}_{\text{Momentary Surprise}}.

其中， $S_t$ 是动量项，记录跨时间序列的惊讶记忆。公式中的 $\eta_t$ 是 input dependent 的惊讶衰减函数，控制惊讶随时间的衰减方式； $\theta_t$ 控制瞬时惊讶在最终惊讶度量中的权重。这种数据依赖性非常重要，因为前一个 token 的惊讶可能需要影响下一个 token 的惊讶，但这只有在 token 相关且处于相同上下文中时才有效。 $\eta$ 是 input dependent 的就意味着模型可以通过这次输入思考，自己是应该完全忘掉之前的惊讶度情况（ $\eta_t\rightarrow 0$ ）还是完全依赖之前的情况 $\eta_t\rightarrow1$ 。

Objective

上面有一个 loss function $\ell(\cdot;\cdot)$ 是记忆模块需要在 Test Time Training 中学习的目标函数。换而言之，记忆模块相当于一个 meta module，基于 loss function 学习一个函数。

本文定义：

k_t = x_t W_K, \quad v_t = x_t W_V,

\ell(M_{t-1}; x_t) = \| M_{t-1}(k_t) - v_t \|_2^2.

还是一个类似 transformer 的结构，是一个关联记忆，目标是将过去的数据存储为 key-value 对。

需要注意的是，类似于元学习模型，记忆模块的训练发生在内部循环中，因此上述损失函数中的参数 $W_K$ 和 $W_V$ 是超参数。相应地，在内部循环中，我们优化 $M$ 的权重，而在外部循环中，我们优化整个架构的其他参数。

Forgetting Mechanism

给定下一个 token $x_t$ ，修改更新规则如下：

M_t = (1 - \alpha_t) M_{t-1} + S_t,

S_t = \eta_t S_{t-1} - \theta_t \nabla \ell(M_{t-1}; x_t),

$\alpha$ 控制了衰减的情况。

Memory Architecture

用 MLP，认为用一个更简单的架构可以避免讨论一些复杂的问题，但是更加复杂的架构可能会有更有趣的表现。

当使用向量值或矩阵值记忆时，记忆模块会压缩过去数据并将其适配到一个线性结构中。从元学习或在线学习的角度来看，使用矩阵值记忆 $M = W \in \mathbb{R}^{d_{\text{in}} \times d_{\text{in}}}$ 等价于优化以下损失函数：

\ell(W_{t-1}; x_t) = \| W_{t-1} k_t - v_t \|_2^2,

这是一个在线线性回归目标，因此其最优解假定历史数据的潜在依赖关系是线性的。然而，我们认为深度记忆模块（即 $L_M \geq 2$ ）是必要的。理论研究表明，至少两层的 MLP 比线性模型严格更具表达能力。

Retrieving a Memory

形式化地，给定输入 $x_t$ ，我们使用一个线性层 $W_Q$ 将输入投影为查询 $q_t = x_t W_Q$ ，并通过以下公式从记忆中检索相应（或有用）的信息 $y_t$ ：

y_t = M^*(q_t).

3.2. How to Parallelize the Long-term Memory Training

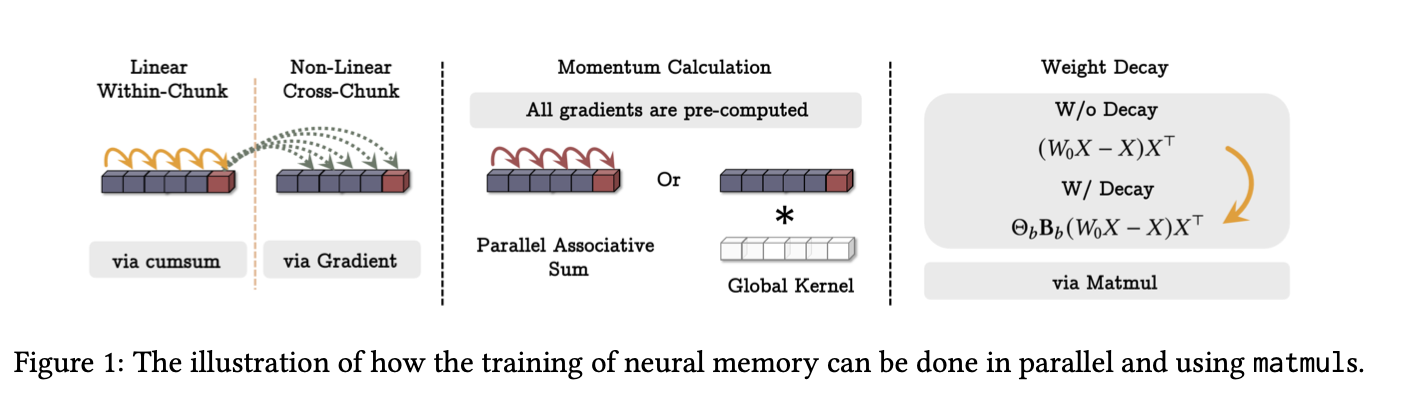
正如上述讨论，我们的长期记忆模块的设计等价于通过优化关联记忆损失函数 $\ell(M_{t-1}; x_t) = \|M_{t-1}(k_t) - v_t\|_2^2$ ，结合动量和权重衰减进行训练的元模型。因此，从理论上讲，训练长期记忆模块需要 O (N) 的浮点运算（FLOPs），其中 N 是序列长度。然而，在实际操作中，为了充分利用硬件加速器（例如 TPUs 和 GPUs），我们需要对训练过程进行并行化，并将其张量化以更多地使用矩阵乘法操作（matmuls）。

将序列分割为一系列小 batch（ $b\ge 1$ ），在这些小 batch 上的梯度下降写作：

M_t = (1 - \alpha_t)M_{t-1} - \theta_t \nabla \ell(M_{t-1}; x_t) = \beta_t M_0 - \sum_{i=1}^t \theta_i \nabla \ell(M_{t{\prime}}; x_i),

其中 $t' = t - \text{mod}(t, b)$ ，且 $\beta_i = \prod_{j=1}^i (1 - \alpha_j)$ .简单考虑 $t=b$ 的情况，那么 $t'=0$ ,，并且认为 $M_t=W_t$ （也就是只有一层，是个线性变换），则有：

\nabla \ell(W_0; x_t) = (W_0 x_t - x_t)x_t^\top \quad \Rightarrow \quad \sum_{i=1}^b \theta_i \nabla \ell(W_0; x_i) = \Theta_b B_b (W_0 X - X) X^\top,

其中 $\Theta_b = \text{diag}(\theta_1, \theta_2, \ldots, \theta_b) ，$ $B_b$ 是基于 $\beta_i$ 类似定义的对角矩阵。需要注意的是，我们无需存储所有的 $\Theta_{kb}$ 和 $B_{kb}$ （对于 $k = 1, \ldots, N/b$ ），而是只为每个块存储这些矩阵，从而减少内存占用。

Parameters as the Function of Chunks

直接把 $\alpha_t, \theta_t, \eta_t$ 设置成 $x_t$ 的函数训练起来有点慢，所以变成对每个块都共享相同的参数。这样，学习的过程中 $\eta$ 和 $\theta$ 在块内都可学习，但 $t$ 维度上不变，这个系统变成一个线性时不变系统，可以直接用卷积算。

但是这篇文章做实验的时候没有做这种操作。

3.3. Persistent Memory

长期记忆模块也可以被视为一种上下文记忆，意味着其输出完全依赖于上下文。因此，除了长期记忆之外，我们还使用一组可学习但与输入无关的参数作为任务相关的记忆。在文献中，这种类型的记忆被称为持久记忆 或元记忆。

当 $N_p \geq 1$ 时，我们使用可学习参数 $P = \{p_1, p_2, \ldots, p_{N_p}\}$ ，并将其附加到序列的开头。对于一个上下文窗口大小为 $N$ 的序列，我们将输入修改为：

x_{\text{new}} = p_1 p_2 \ldots p_{N_p} || x,

其中 $||$ 表示拼接操作。

Memory Perspective

That is, mastering a task requires the memorization of the knowledge that how the task
can be done, and these parameters are responsible for storing such knowledge.

Feedforward Network Perspective

在 Transformer 架构中，注意力模块后面通常接有全连接层，这些层被证明与注意力权重类似，但具有数据无关的参数。Sukhbaatar, Grave 等人指出，将全连接层中的 ReLU 替换为 Softmax，可以得到类似于注意力的权重，这些权重是数据无关的：

\text{FFN}(x) = W_V \, \text{Softmax}(W_K x).

实际上，当 $W_K$ 和 $W_V$ 是输入无关的时，它们的作用类似于注意力模块中的 $K$ 和 $V$ 矩阵。持久记忆权重被期望具有相同的功能，也就是说，将它们应用于序列的开头部分，可以得到输入无关的注意力权重。

Technical Perspective

具有因果掩码的注意力机制对序列中初始令牌存在隐含偏置，因此注意力权重几乎总是对初始令牌高度激活，这可能损害模型性能。从技术角度看，这些位于序列开头的可学习参数可以通过更有效地重新分配注意力权重来缓解这一问题。通过引入持久记忆模块，模型能够更灵活地对任务相关信息进行建模，同时缓解因注意力偏置而引发的性能瓶颈。

4. How to Incorporate Memory?

一个尚未解答的重要问题是：如何有效且高效地将设计的神经记忆模块整合到深度学习架构中？正如之前讨论的，从记忆的视角看，Transformer 中的 $K$ 和 $V$ 矩阵对可以被解释为关联记忆模块。由于其对依赖关系的精确建模及其有限的上下文窗口，这些模块可以被看作短期记忆模块，专注于当前的上下文窗口大小。另一方面，我们的神经记忆模块能够持续从数据中学习，并将其存储到权重中，可以扮演长期记忆的角色。

设计了三种不同的架构进行对比。

4.1. Memory as a Context

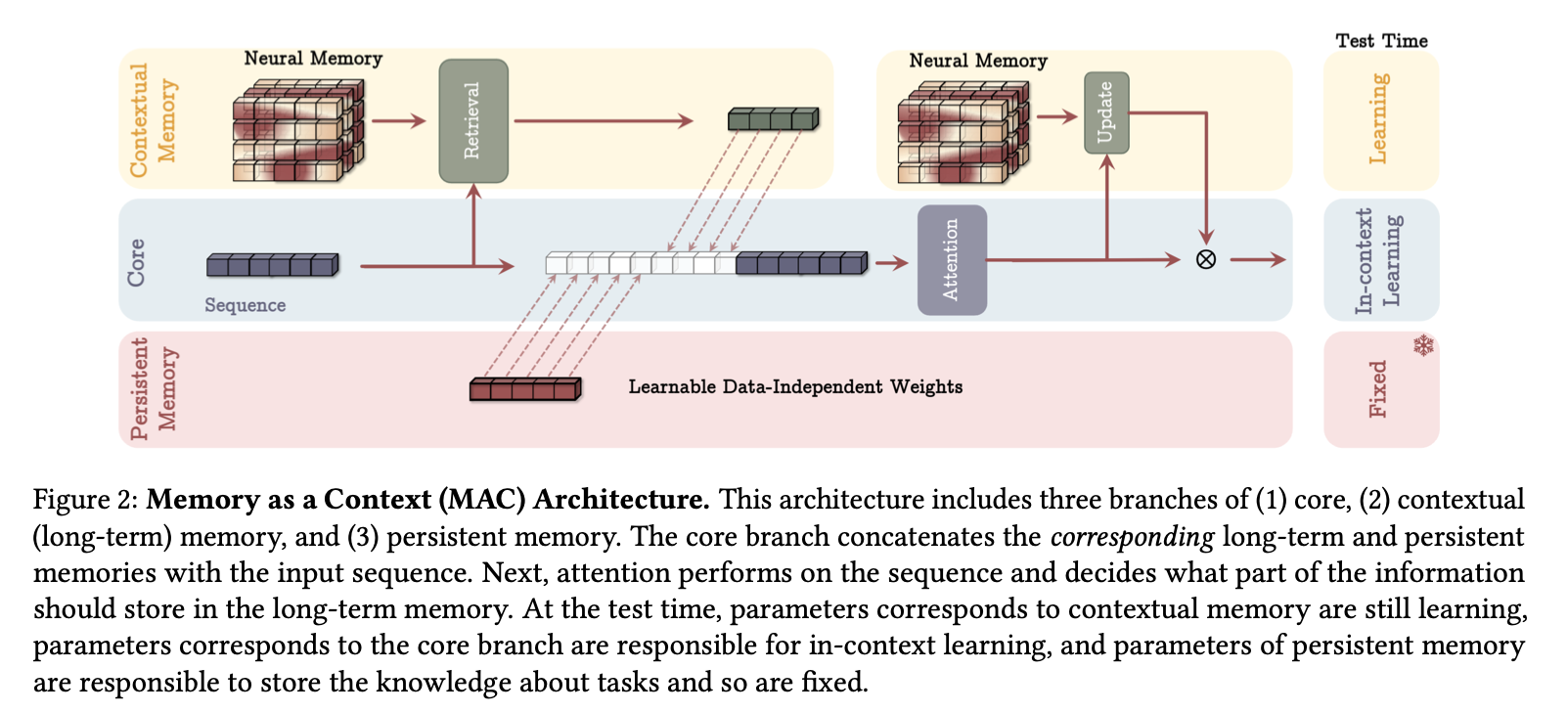
对于一个长序列 $x \in \mathbb{R}^{N \times d_{\text{in}}}$ ，我们首先将其分割为固定大小的片段 $S(i) （ i = 1, \ldots, N/C ）$ 。对于输入片段 $S(t)$ ，我们将其视为当前上下文，将其前面的片段视为历史信息。因此，令 $M_{t-1}$ 为片段 $S(t)$ 之前的长期记忆状态，我们将输入上下文作为查询来从长期记忆 $M_{t-1}$ 中检索相应的信息：

h_t = M^*_{t-1}(q_t),

其中 $q_t = S(t) W_Q$ 。接下来，我们将这一历史信息与持久记忆参数一起作为输入序列传递给注意力模块：

\tilde{S}(t) = p_1 p_2 \ldots p_{N_p} || h_t || S(t),

y_t = \text{Attn}(\tilde{S}(t)).

我们随后使用 $y_t$ 来更新下一个片段的长期记忆模块及最终输出：

M_t = M_{t-1}(y_t),

o_t = y_t \otimes M^*_t(y_t),

其中 $\otimes$ 表示非线性结合操作。在上述操作中，我们通过前向传播来更新 $M_{t-1}$ 的权重。

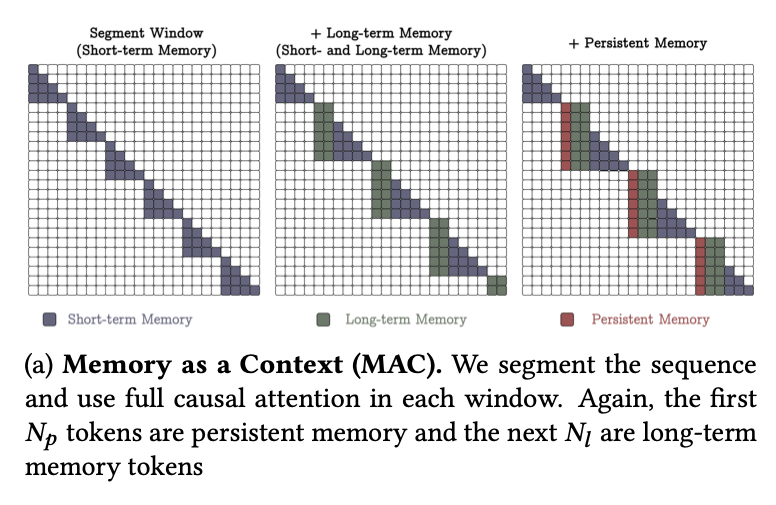
该架构具有以下三个关键优势：

注意力机制通过同时考虑历史和当前上下文，能够决定在当前数据下是否需要长期记忆的信息
注意力模块帮助长期记忆仅存储当前上下文中的有用信息。并非所有片段中的令牌都是有用的，记住所有令牌可能导致记忆溢出。因此，注意力机制有助于记忆识别有用信息，从而更好地管理记忆容量。
在测试时：
- 持久记忆参数是固定的，因为它们编码了任务知识，不应更改；
- 注意力模块的权重是上下文学习器；
- 长期记忆模块仍在测试时学习（记忆）信息。也就是说，即使在测试时，我们仍然更新神经记忆的权重，这些权重编码了远久的抽象信息。

4.2. Gated Memory

\tilde{x} = p_1 p_2 \ldots p_{N_p} || x,

y = \text{SW-Attn}^*(\tilde{x}),

o = y \otimes M(\tilde{x}),

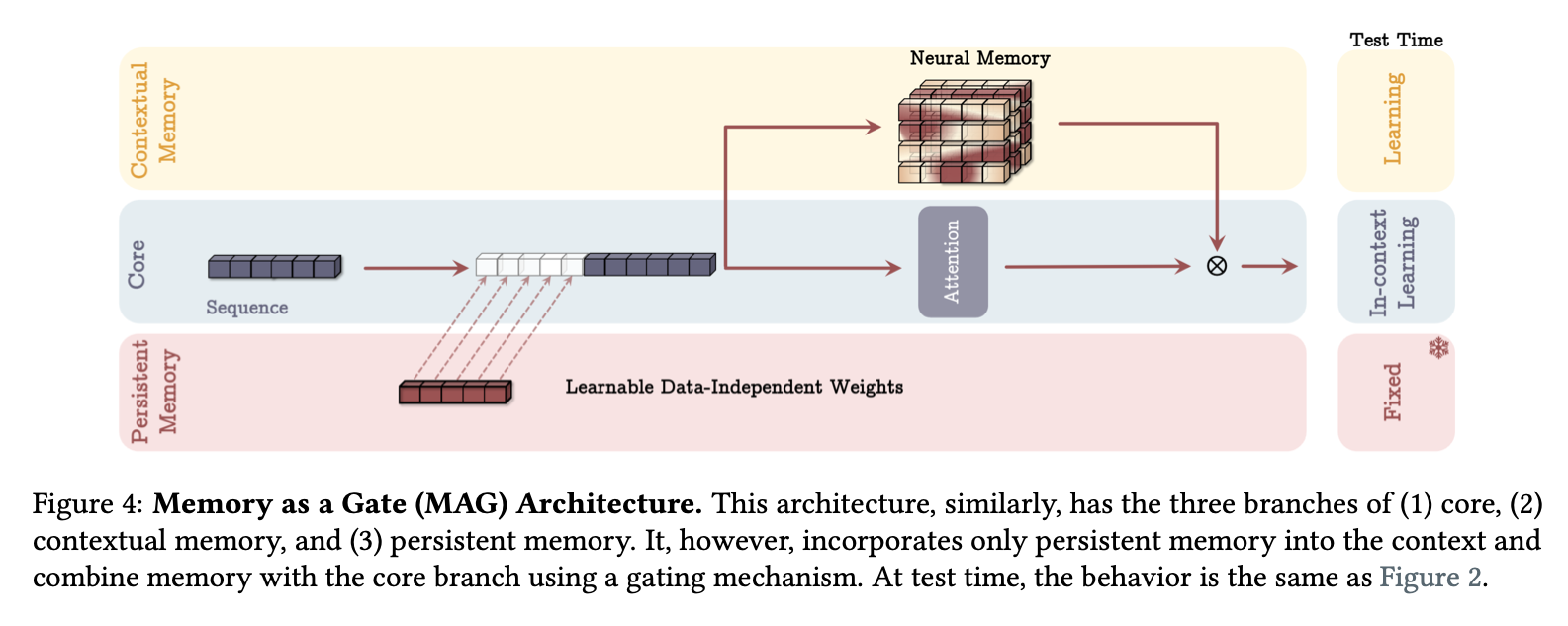
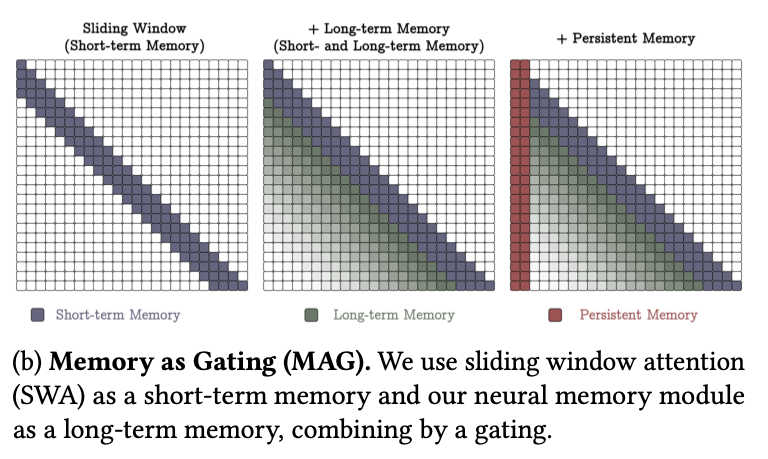
4.3. Memory as a Layer

\tilde{x} = p_1 p_2 \ldots p_{N_p} || x,

y = M(\tilde{x}),

o = \text{SW-Attn}(y),

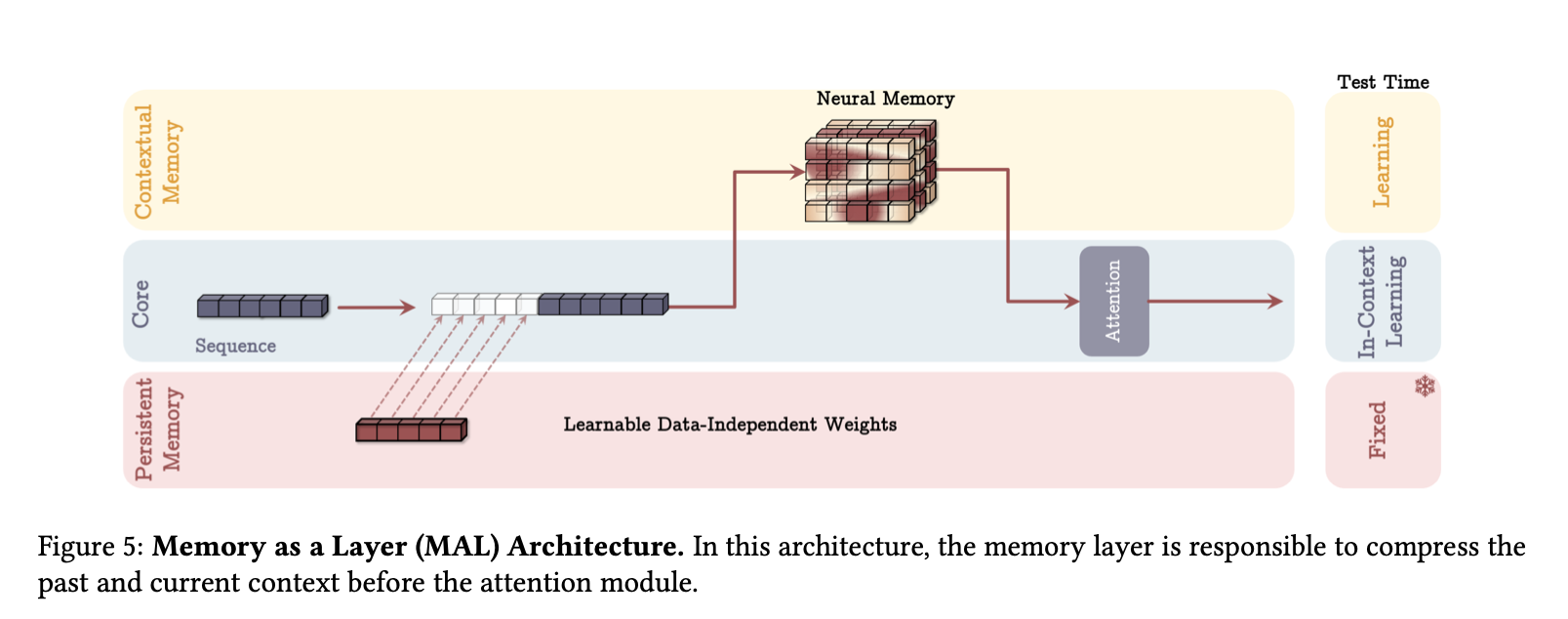
Memory without Attention

尽管上述讨论将 MAL 视为 LMM 与注意力的顺序组合，但 MAL 的一个简单变体是将 LMM 视为没有注意力的序列模型。从记忆的视角看，正如第 1 节讨论的，我们期望记忆系统的每个部分能够独立工作，即使其他组件受到干扰。因此，即使没有短期记忆（如注意力），长期记忆模块也应该是一个强大的模型。我们在实验中将这一变体称为 LMM 或 Titans (LMM)。

4.4. Architectural Details

为了简化讨论和清晰表达，我们避免涉及诸如使用残差连接、线性层的门控和归一化等实现细节。在所有模块中，我们都使用了残差连接。在实现中，我们采用 SILU 激活函数作为查询、键和值的非线性激活函数，并使用 $\ell_2\text{-norm}$ 对 Q 和 K 进行归一化。

Convolution

借鉴最近的现代线性递归模型，我们在每次投影查询、键和值之后引入了一个一维深度可分卷积层。尽管这些 1D 卷积对性能的提升并不显著，但它们已被证明能够改善模型性能，同时具有计算效率。

Gating

我们还遵循了近期架构的做法，在最终输出投影之前，使用线性层进行归一化和门控操作。这种设计可以进一步增强模型的稳定性和表现力。

定理 4.1. 与 Transformer、对角线线性递归模型和 DeltaNet 不同，这些模型都被限制在 $TC^0$ 中，而 Titans 能够解决超出 $TC^0$ 的问题。这意味着，在状态跟踪任务中，Titans 的理论表达能力比 Transformer 和大多数现代线性递归模型更强。

5. Experiments

接下来，我们将评估 Titans 及其变体在语言建模、常识推理、大海捞针（needle-in-a-haystack）、DNA 建模和时间序列预测等任务中的性能。本节将探讨以下五个关键问题：

相比基线模型，Titans 在下游任务中的表现如何？
Titans 的实际上下文长度能达到多少？
随着上下文长度增加，Titans 的性能如何变化？
记忆深度对性能和效率有何影响？
Titans 的各个组件如何影响整体性能？

5.1. Experimental Setup

评估上面提到的 MAC，MAG，MAL 三种，在 170M，340M，400M，760M 这些参数量上。对比对象包括 Transformer++, RetNet, Mamba, DeltaNet, GPT-4 等。使用 LLama2 的分词器（词汇表大小为 32K），训练序列长度为 4K tokens。优化器采用 AdamW，学习率为 4e-4 ，使用余弦退火调度，批量大小为 50 万 tokens，权重衰减设置为 0.1。

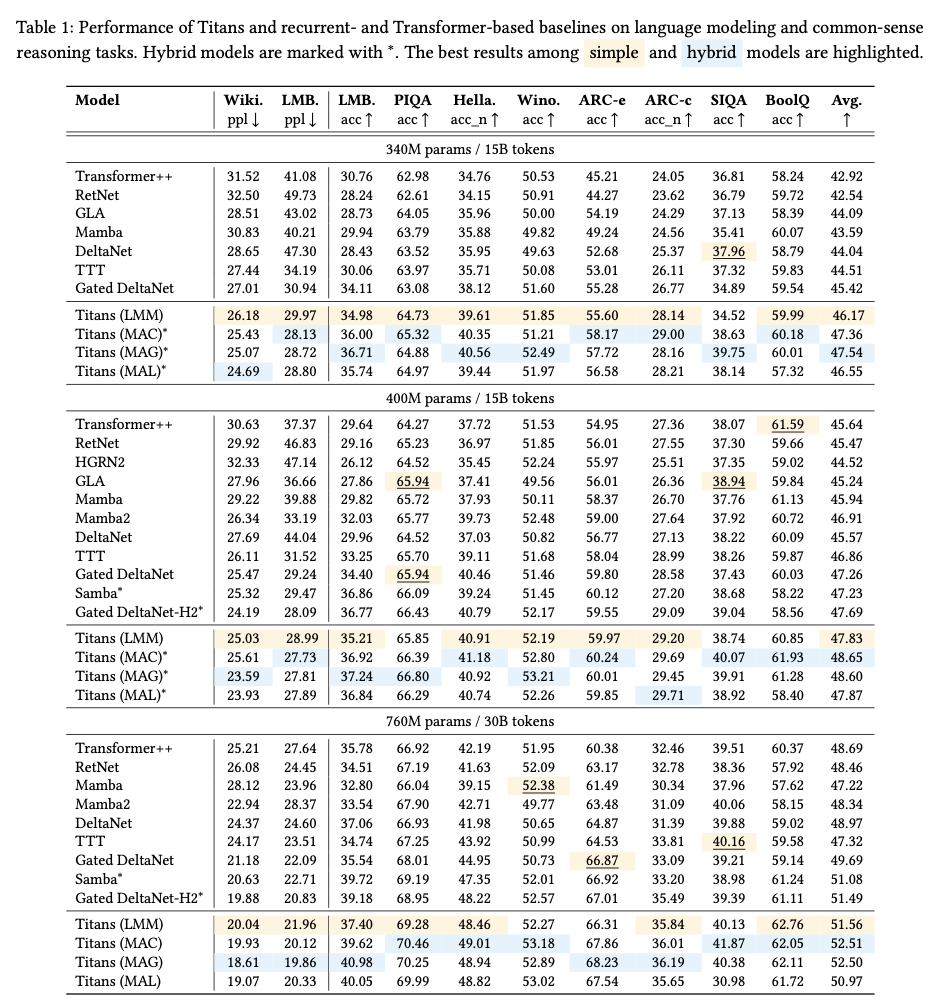
5.2. Language Modeling

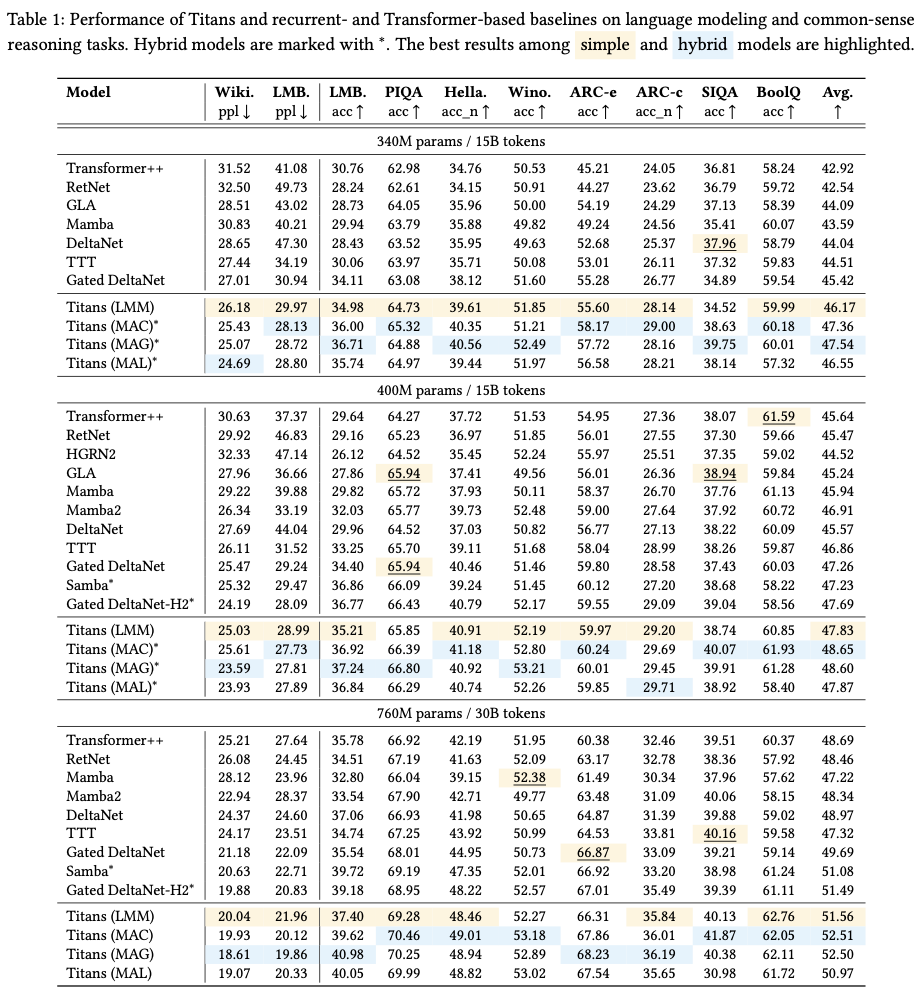
MAC 和 MAG 的性能接近，但在处理数据中的长依赖关系时，MAC 表现更优。而 MAC 和 MAG 均优于 MAL，这表明模型设计对性能有重要影响。

和同类工作比达到 SOTA，尤其是比 TTT 更好。

5.3. Needle in a Haystack

展示长建模能力。MAC 最好。

5.4. BABILong Benchmark

任务中，模型需要跨超长文档中分布的多个事实进行推理。

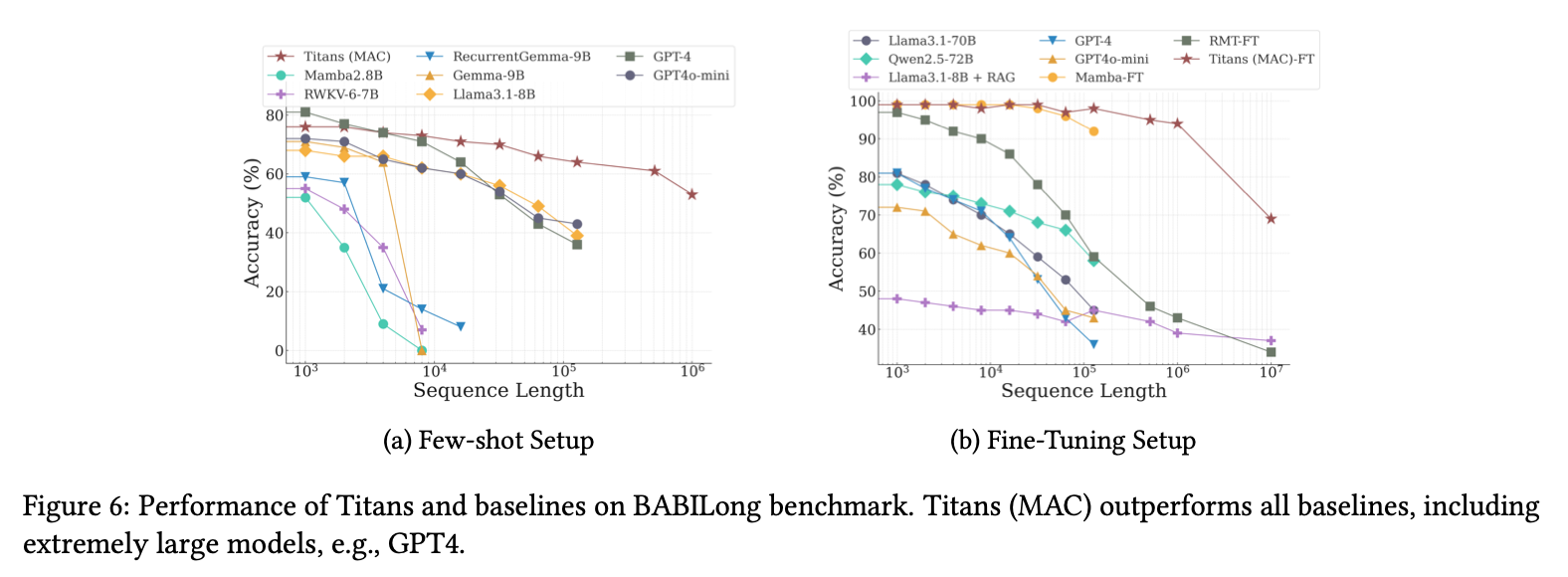
做了 few shot 和大规模训练过两种实验。

5.5. The Effect of Deep Memory

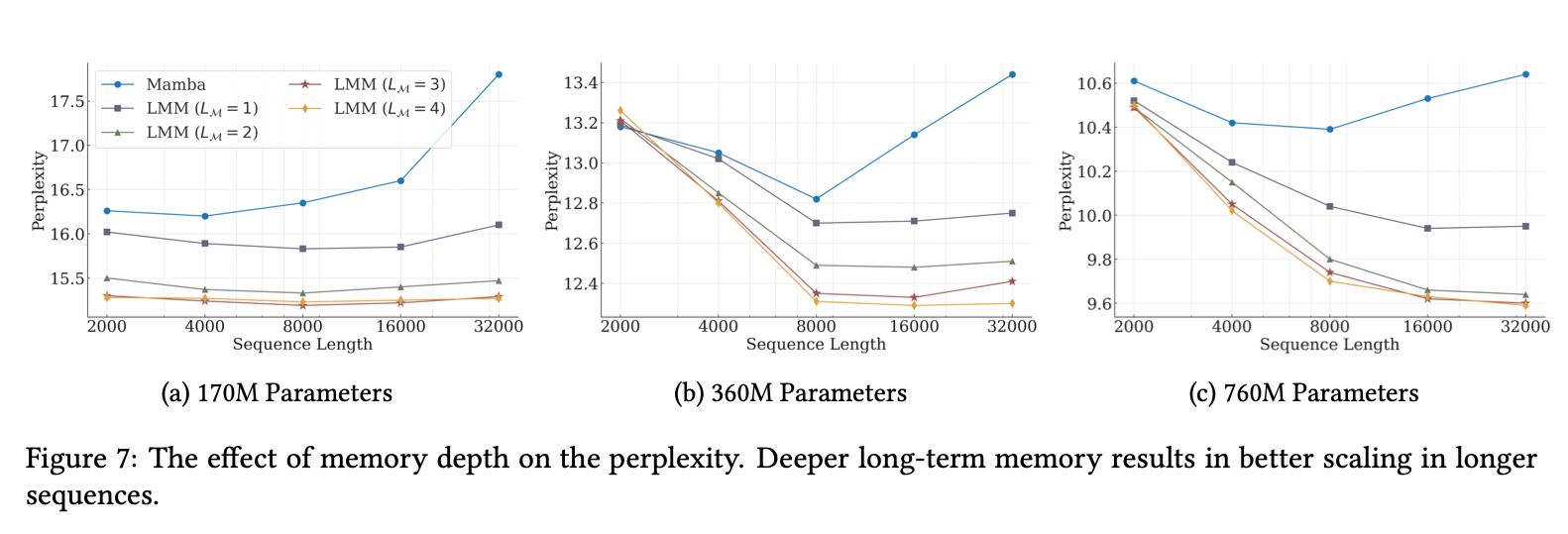
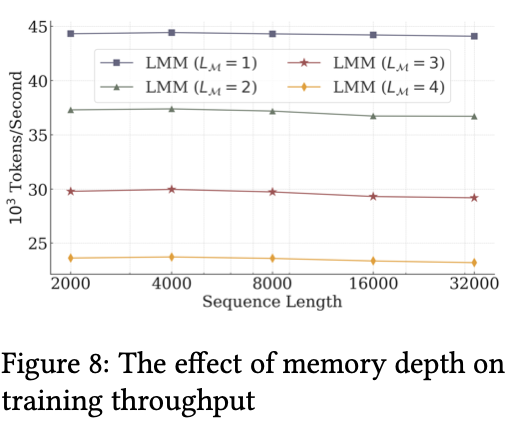
把 Memory 模块多叠几层更好，不过对 throughput 影响挺大。

5.6. Time Series Forecasting

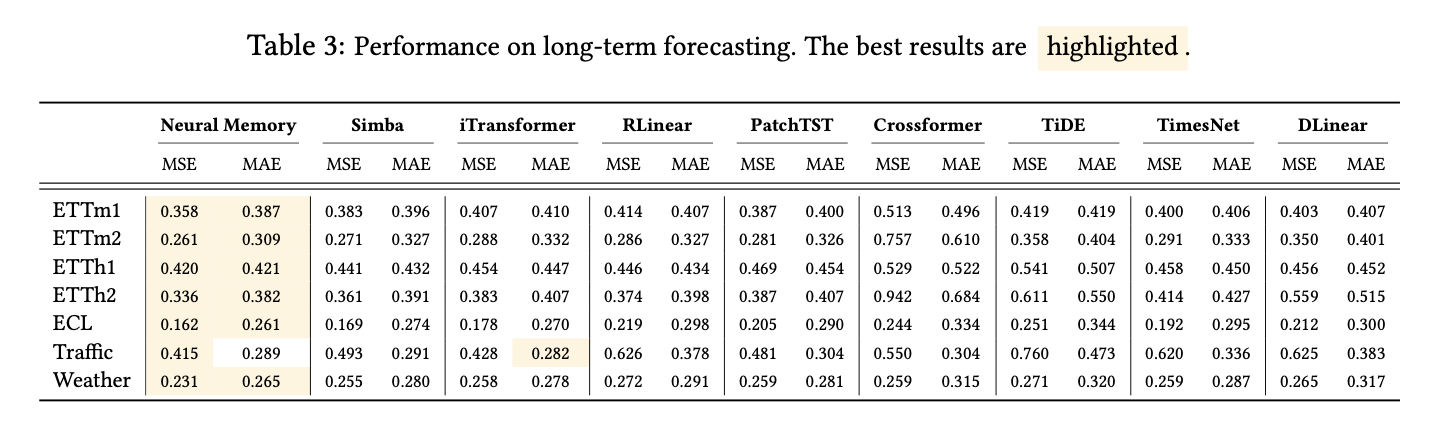
5.7. DNA Modeling

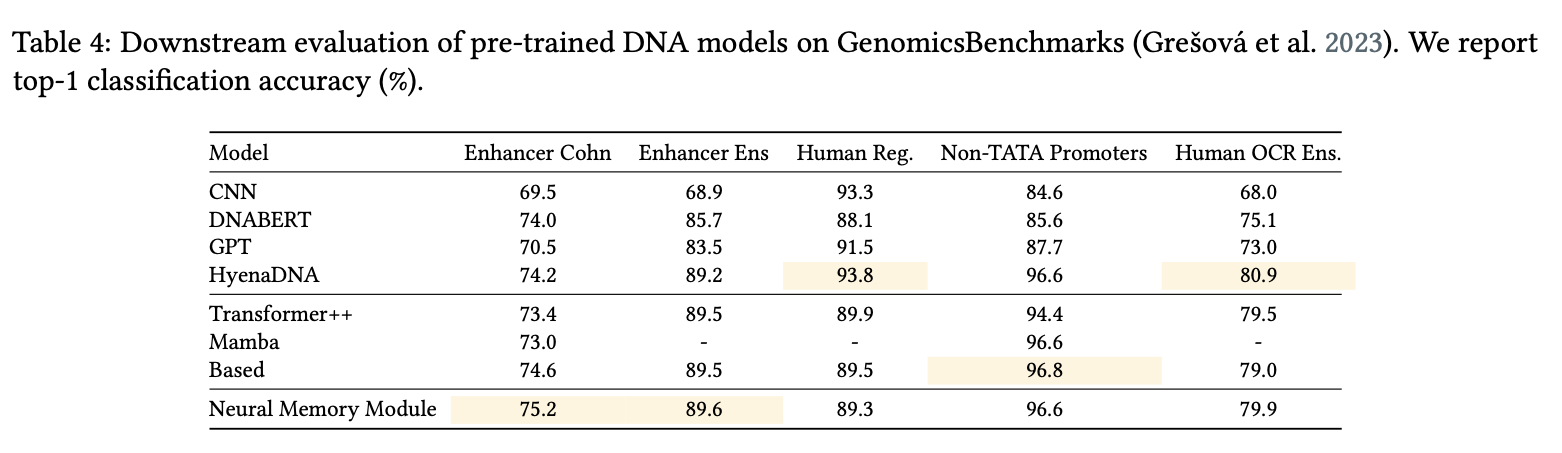
5.8. Efficiency

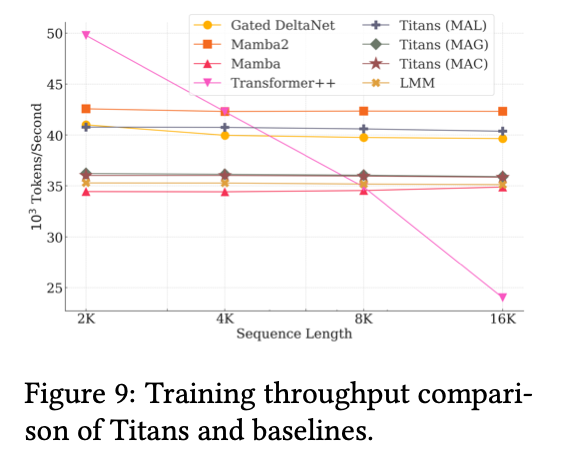
比 Mamba 之类的慢，文章认为是自己的优化之类的不如这些已经提出来的方法，并且更新记忆的过程确实复杂一些。

5.9. Ablation Study

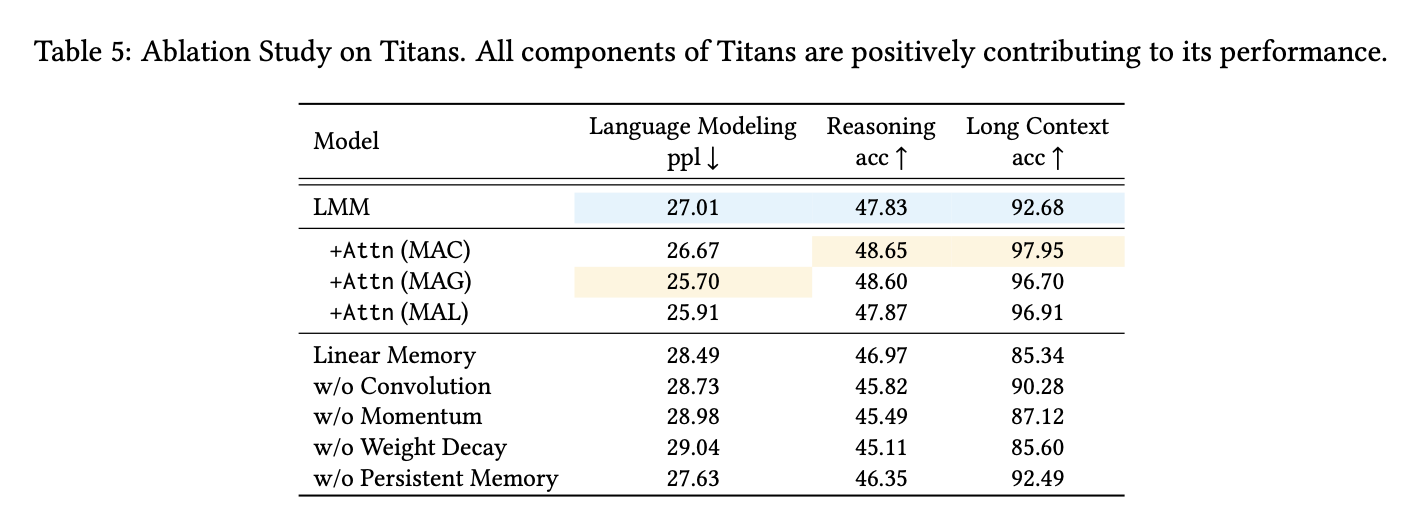
所有组件均对性能有积极贡献，其中权重衰减、动量、卷积和持久记忆对性能提升的贡献最大。

6. Conclusion

在本文中，我们提出了一种神经长期记忆模块，作为一种元上下文学习器（meta in-context learner），能够在测试时学习记忆。该神经记忆模块本质上是一种递归模型，能够自适应地记忆那些更具惊讶性或接近惊讶的 tokens。与现代递归模型相比，该模块具有更强的记忆更新和存储机制。基于此记忆模块，我们提出了 Titans 架构，包括三种变体：1. 将记忆模块作为 Context；2. 将记忆模块作为 Gating；3. 将记忆模块作为网络的 Layer。我们在多种任务中的实验验证了 Titans 的有效性，相较于 Transformers 和最新的线性递归模型，Titans 在处理超长上下文时表现更为出色。例如，Titans 能够扩展到超过 200 万的上下文窗口，并在准确性方面优于基线模型。目前，Titans 已在 PyTorch 和 JAX 中实现，我们计划很快开源用于训练和评估模型的代码。