摘要： 后训练量化（PTQ）是一种加速大语言模型（LLM）推理的有效技术。然而，现有工作在推理过程中仍需要大量浮点（FP）操作，包括额外的量化和反量化，以及 RMSNorm 和 Softmax 等非线性操作。这一限制阻碍了LLM在边缘设备和云设备上的部署。在本文中，我们发现LLM实现全整数量化的主要障碍在于线性和非线性操作中跨通道和跨标记的激活大幅波动。为了解决这个问题，我们提出了I-LLM，一种为LLM量身定制的全整数全量化PTQ新框架。具体来说，(1) 我们开发了全平滑块重建（FSBR），以积极平滑所有激活和权重的跨通道变化。(2) 为了缓解跨标记变化引起的性能下降，我们引入了一种称为动态整数矩阵乘法（DI-MatMul）的新方法。该方法通过动态量化输入和输出的全整数操作，实现了全整数矩阵乘法的动态量化。(3) 我们设计了DI-ClippedSoftmax、DI-Exp和DI-Normalization，利用位移操作有效执行非线性运算，同时保持精度。实验结果表明，我们的I-LLM在精度上可与FP基线媲美，并优于非整数量化方法。例如，I-LLM能够在W4A4设置下运行，且精度损失可忽略不计。据我们所知，我们是首个弥合全整数量化与LLM之间差距的研究。我们已将代码发布在anonymous.4open.science，旨在推动该领域的发展。

1. Intro

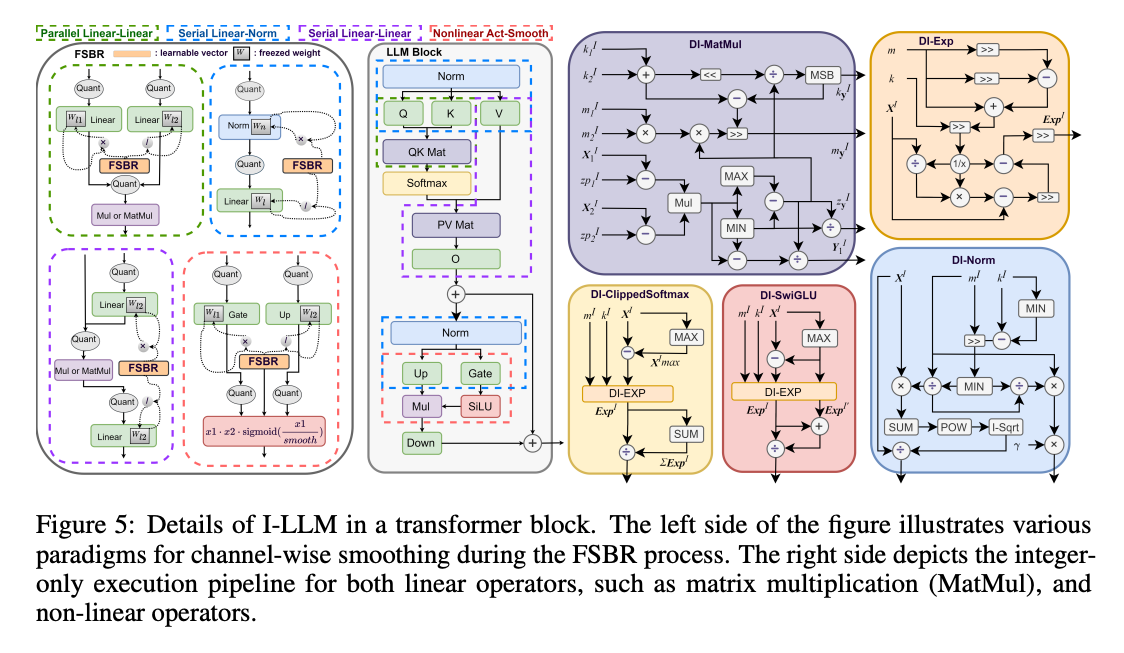
之前的LLM PTQ经常要做伪量化，做实际计算的时候还是用的浮点型。虽然降低了数据传输和带宽的需求，但是实际上没有减少计算量（因为计算的时候还是float）。

LLM量化的Integer-Only的工作很少，之前的工作主要集中在CNN，后来有对Bert和ViT的Integer-Only的量化。LLM integer only的工作这是第一篇。

Contribution：

identify the primary obstacle to integer-only quantization for LLMs lies in the large fluctuation of activations across channels and tokens in both linear and no-liner operators.
propose FSBR to effectively reduces disparities among all suitable activation-activation and activation-weight pairs
DI-MatMul, which enables dynamic quantization on input and output though full-integer matrix multiplication.
DI-Exp, DI-ClippedSoftmax, DI-Norm that harness the power of bit shifting to replace complex mathematical computations within the non-linear functions of LLMs
To the best of our knowledge, this work represents the first attempt to utilize integer-only quantization for LLMs, enabling their deployment on edge devices that lack floating-point capabilities. Experiments demonstrate remarkable accuracy when compared to SOTA non-integer quantization techniques, e.g., I-LLM on LLAMA-13b achieves an approximate 20% reduction in perplexity

LLMs Quantization： 从优化矩阵乘、activation outliers到KV Cache、ZeroQuant这样包含一部分系统的工作，QAT和PTQ都有。这篇文章是一个PTQ的工作，对于超大的LLM来讲QAT可能带来的fine-tuning开销太大了。

Integer-only Quantization: dyadic arithmetic on CNN and transformer，比如I-BERT，但是在比如GELU这样的操作里面还是会包含FP计算。I-ViT是Integer-Only的ViT，但是在LLM的数据和情况上是否有效还不清楚。

3. Method

Challenges of Integer-Only Quantization for Large Language Models：

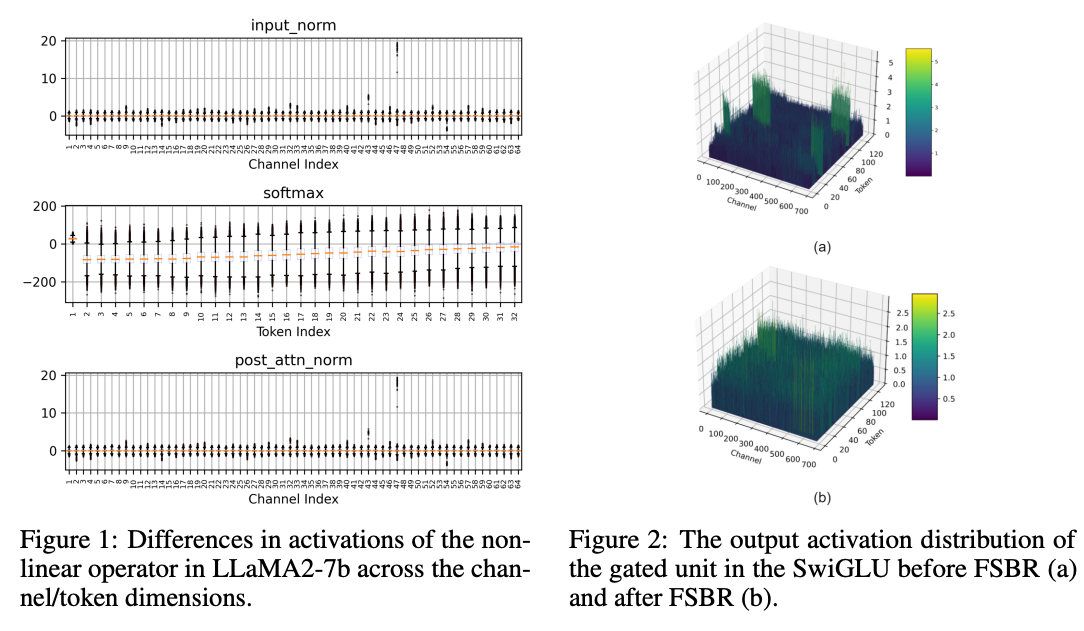
Quantizing the activation of LLMs, especially those originating from non-linear operators, ** poses a formidable challenge.** As evidenced in Fig 1, the divergence in these non-linear activations often surpasses that of linear operators, particularly pronounced in models such as LLaMA. Previous methods have failed to address these non-linear activations, and straightforwardly quantizing non-linear layers may lead to substantial accuracy degradation.
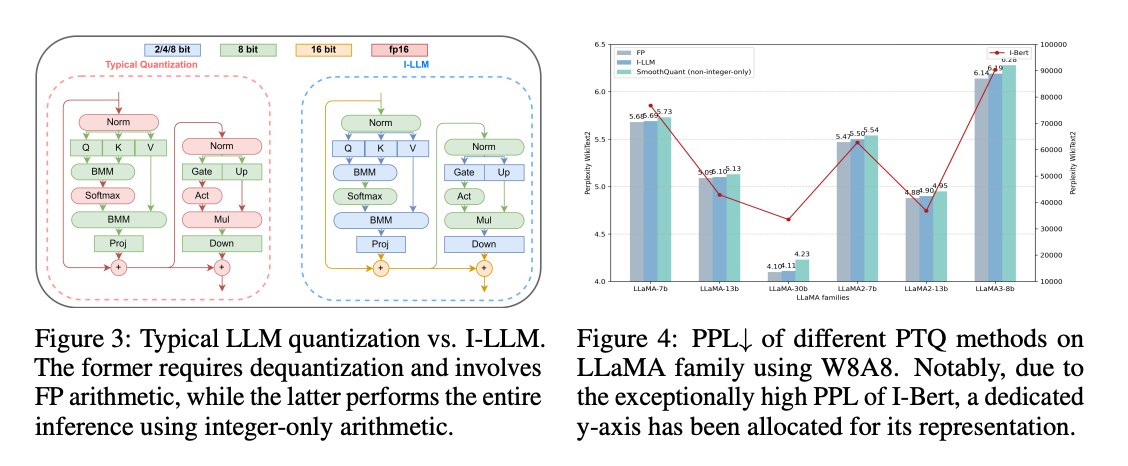
prior integer-only quantization techniques have overlooked the distinctive traits of LLMs , including divergent activation scales and the substantial overhead of loading large-scale weights. Even the W8A8 method introduced in I-BERT can lead to catastrophic outcomes, as shown in Fig 4, let alone more aggressive quantization methods like W6A6 or W4A4.

3.1. Basic Mathematical Notations

$X$ ：矩阵 $x$ ：向量 $x^I$ ：Integer-only的向量
$Q()$ ：量化函数
$\lfloor\cdot\rfloor$ ：向下取整 $\lceil\cdot\rceil$ ：向上取整 $\lfloor\cdot\rceil$ 最近取整
$\otimes$ ：逐元素乘法 $\oslash$ ：逐元素除法

3.2. Fully-Smooth Block-Recontruction(FSBR)

\begin{align*}\text{SwiGLU}\left(x, W, V, b, c\right)&=\text{SiLU}\left(xW+b\right)\otimes\left(xV+c\right)\\&=x1\otimes x2\otimes \sigma(x1)\end{align*}

$W, V\in R^{ic\times oc}$ 是权重， $b$ 是bias， $x1=xW+b, ~x2=xV+c$ 。 $\text{SiLU}$ 是SigmoidWeighted Linear Unit, $\sigma$ 是sigmoid激活函数。

加入一个平滑因子：

\text{SwiGLU}(x, W, V, b, c) = (x1 \odot s) \otimes (x2 \odot s) \otimes \sigma'(x1 \odot s)

然后将因子合并到权重中并且进行量化：

\text{SwiGLU}(x) = \mathcal{Q}(\mathcal{Q}(x)\mathcal{Q}(W') + b') \otimes \mathcal{Q}(\mathcal{Q}(x)\mathcal{Q}(V') + c') \otimes\sigma'(\mathcal{Q}(\mathcal{Q}(x)\mathcal{Q}(W') + b'))

3.3. Dynamic Integer-only MatMul (DI-MatMul)

之前的用移位+低精度乘法实现的总体来讲还是有很多的误差，文章提出一种新的矩阵乘法pipeline，写作：

\bold{Y^I}, s_y, zp^I=\mathcal{M}(s_1, zp_1^I, s_2, zp_2^I, \bold{X_2^I})

$s_1, s_2, s_y$ 是浮点数标量，表示输入、输出和量化步长； $zp_1^I, zp_2^I$ 是整数的零点，然后将前面的浮点数改写成 $m^I/2^{k^I}$ 的形式，就有：

Y^I, m_y^I, k_y^I, zp^I = \mathcal{M}(m_1^I, k_1^I, zp_1^I, X_1^I, m_2^I, k_2^I, zp_2^I, X_2^I)

一次矩阵乘法操作中，

P^I = (X_1^I - zp_1^I)(X_2^I - zp_2^I), \quad Y = P^I \frac{m_1^I m_2^I}{2^{k_1^I + k_2^I}}

近似：

\frac{m_y^I}{2^{k_y^I}} \approx s_y = \frac{(p_{\max}^I - p_{\min}^I) \cdot m_1^I \cdot m_2^I}{(2^n - 1) \cdot 2^{k_1^I + k_2^I}}

为了求得输出的量化尺度，有：

\text{arg} \min_{m_y^I, k_y^I} \left\| \frac{(p_{\max}^I - p_{\min}^I) \cdot m_1^I \cdot m_2^I}{(2^n - 1) \cdot 2^{k_1^I + k_2^I}} - \frac{m_y^I}{2^{k_y^I}} \right\|_1 \quad \text{s.t.} \quad m_y^I, k_y^I \in \{0, 1, 2, \ldots, 255\}

求解其他的有：

k_y^I = \left\lfloor \log_2 \left( \frac{256 \cdot (2^n - 1) \cdot 2^{k_1^I + k_2^I}}{p_{\max}^I - p_{\min}^I} \right) \right\rfloor \\ m_y^I = \left( \frac{(p_{\max}^I - p_{\min}^I) \cdot m_1^I \cdot m_2^I}{n_1} \right) \gg (k_1^I + k_2^I - k_y^I) \\ z_y^I = - \frac{p_{\min}^I \cdot (2^n - 1)}{p_{\max}^I - p_{\min}^I} ，\quad Y^I = \left\lfloor \frac{P^I - p_{\min}^I}{p_{\max}^I - p_{\min}^I} \cdot (2^n - 1) \right\rfloor

感觉就是更复杂的quantization，替换掉了原本的乘法+移位的操作

3.4. Dynamic Non-Linear Integer-only Operations

3.4.1. Dynamic Integer-only Clipped Softmax & Dynamic Integer-only Exponent function

DI-Exp:

e^{x^I \cdot (m_x^I \gg k_x^I)} \approx 2^{x^I \cdot (m_x^I \gg k_x^I) \cdot \log_2 e} = 2^{x^I \cdot m_x^I \cdot \log_2 e \gg k_x^I}

化简得到：

e^{x^I \cdot (m_x^I \gg k_x^I)} \approx 2 \left( 1 - \frac{r^I}{2 \cdot s^I} \right) \gg q^I

计算上面的 $p$ 的时候：

p'_{\min} = \max \left( p_{\min}^I, p_{\max}^I - c^I \right), \quad \text{where } c^I = \frac{m_c^I}{2^{k_c}}

3.4.2. Dynamic Integer-only Normalization & Dynamic Integer-only SwiGLU

DI-Norm:

per channel量化

DI-SwiGLU:

4. Experiments

I-LLM中所有的非线性的算子都是W8A8的，线性算子看配置，可能是W4A8huoqitade .

4.1. Quantitative Results

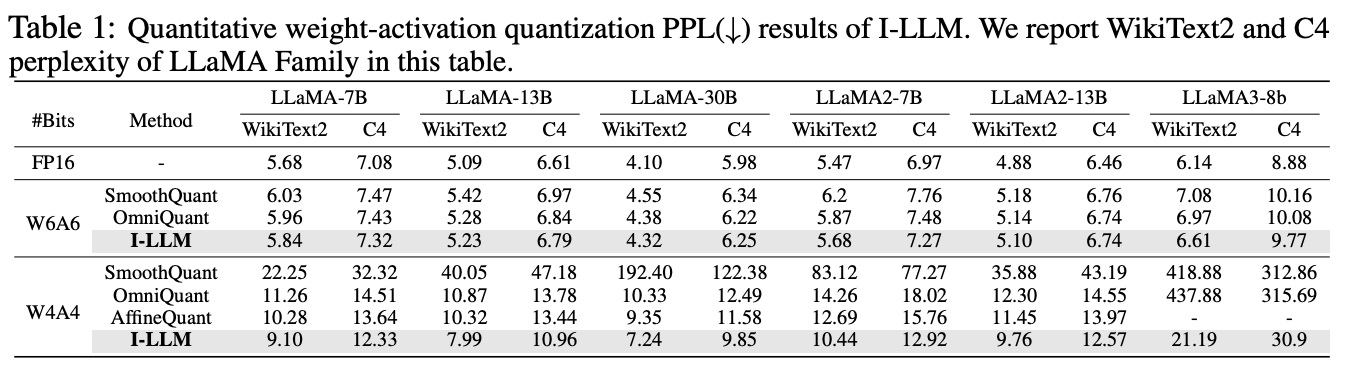
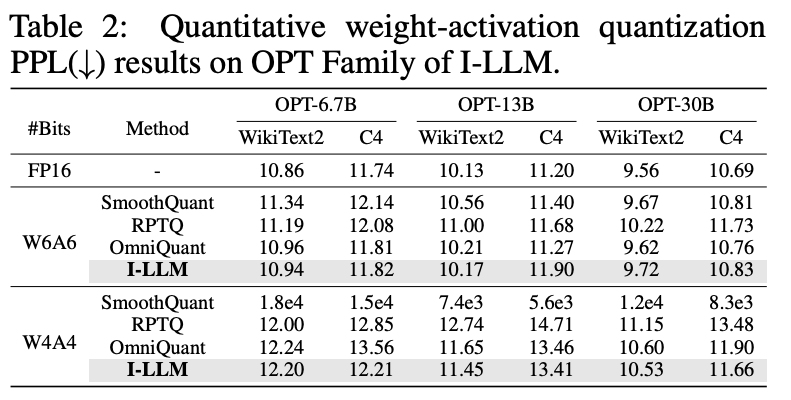
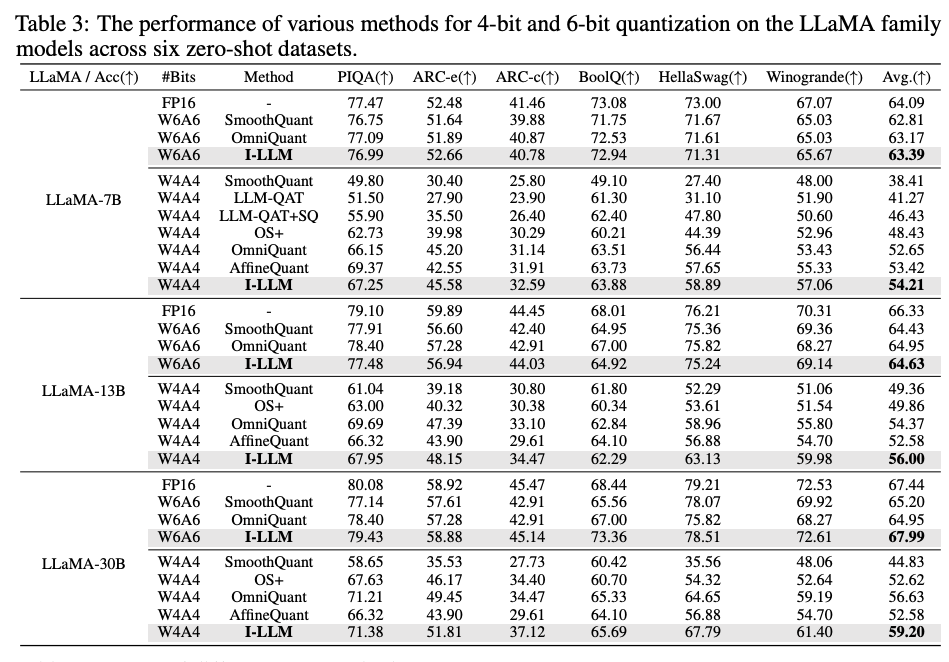
4.2. Ablation Study

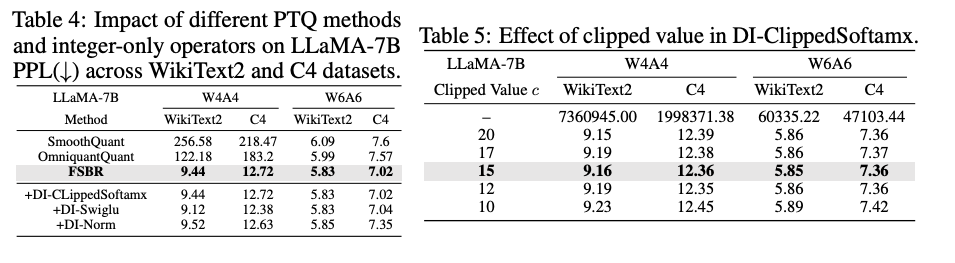
5. Conclusion

感觉和I-ViT、I-BERT几个工作挺像的，提出来的各种DI-OP感觉没有看到特别新的东西。

文章里很多Integer都打成Interger了。

I-LLM: Efficient Integer-Only Inference for Fully-Quantized Low-Bit Large Language Models