摘要： 脉冲神经网络（SNNs）旨在通过引入神经动力学和脉冲特性，在神经形态芯片上实现类脑智能，从而实现高效能量利用。随着深度学习范式的不断演变，传统的编程框架无法满足神经形态计算中不断增加的兴趣、计算资源需求和部署需求。在本文中，我们提出了SpikingJelly框架以应对上述困境。我们贡献了一个面向深度SNNs训练的全栈工具，优化其参数，并在神经形态芯片上部署SNNs。与传统方法相比，SpikingJelly通过混合精度训练、并行计算和语义自动代码生成，加速了深度SNNs的训练。SpikingJelly为在异构系统上综合真正能效高的SNNs铺平了道路，这将丰富神经形态计算的生态系统。

Introduction

人脑的平均功耗仅为20W，借鉴于人脑的SNN在功耗方面可能对ANN而言具有极大的优势。

Emerging spiking deep learning methods

SNN的脉冲发放具有不可导的特性，同时脉冲发放的时空传播过程又非常复杂，导致传统ANN的训练方法在SNN上都无法使用。目前对SNN的训练方法无监督的包括Hebbian学习、尖峰时间依赖性可塑性（STDP）及其变种；有监督的有SpikeProp、Tempotron、ReSume和SPAN，其性能优于生物学上合理的无监督方法。然而，这些方法有限。大多数基于SpikeProp的方法仅允许尖峰神经元发射不超过一个尖峰，而Tempotron、ReSume和SPAN无法训练超过一层的SNNs。

目前常用的方法一种是替代梯度，一种是直接从ANN转换到SNN，两种方法都取得了一定的成果，让SNN能够达到的性能大幅度提升。

Demands for frameworks

之前ANN的普及和Tensorflow、Torch这样完备的框架有很大关系，因为研究者不再需要关注复杂的底层实现。但是在SNN目前已经有的框架，还主要是NEURON、NEST、Brain1/2这样的生物或者医学使用的框架，可以在很细粒度下模拟神经元的发放和传播过程，但既没有自动的反向传播功能，设计上也不是用来解决SNN中的问题的。Nengo、SpykeTorch和BindsNET使用的简化神经元比详细神经元具有更少的ODEs。由于简化神经元带来的低计算复杂性，这些框架可以实现一些初级的机器学习和强化学习算法，但仍然缺乏现代深度学习SNNs的能力。

要制作一个更加好的SNN框架，应该具有以下三个优点：

利用且加速基于Spike的操作；
支持在CPU/GPU这样的现代设备，或者支持SNN计算的硬件如True North、Loihi上部署；
提供用于构建、训练和分析深度SNNs的全栈工具包。

SpikingJelly: A modern framework for spiking deep learning

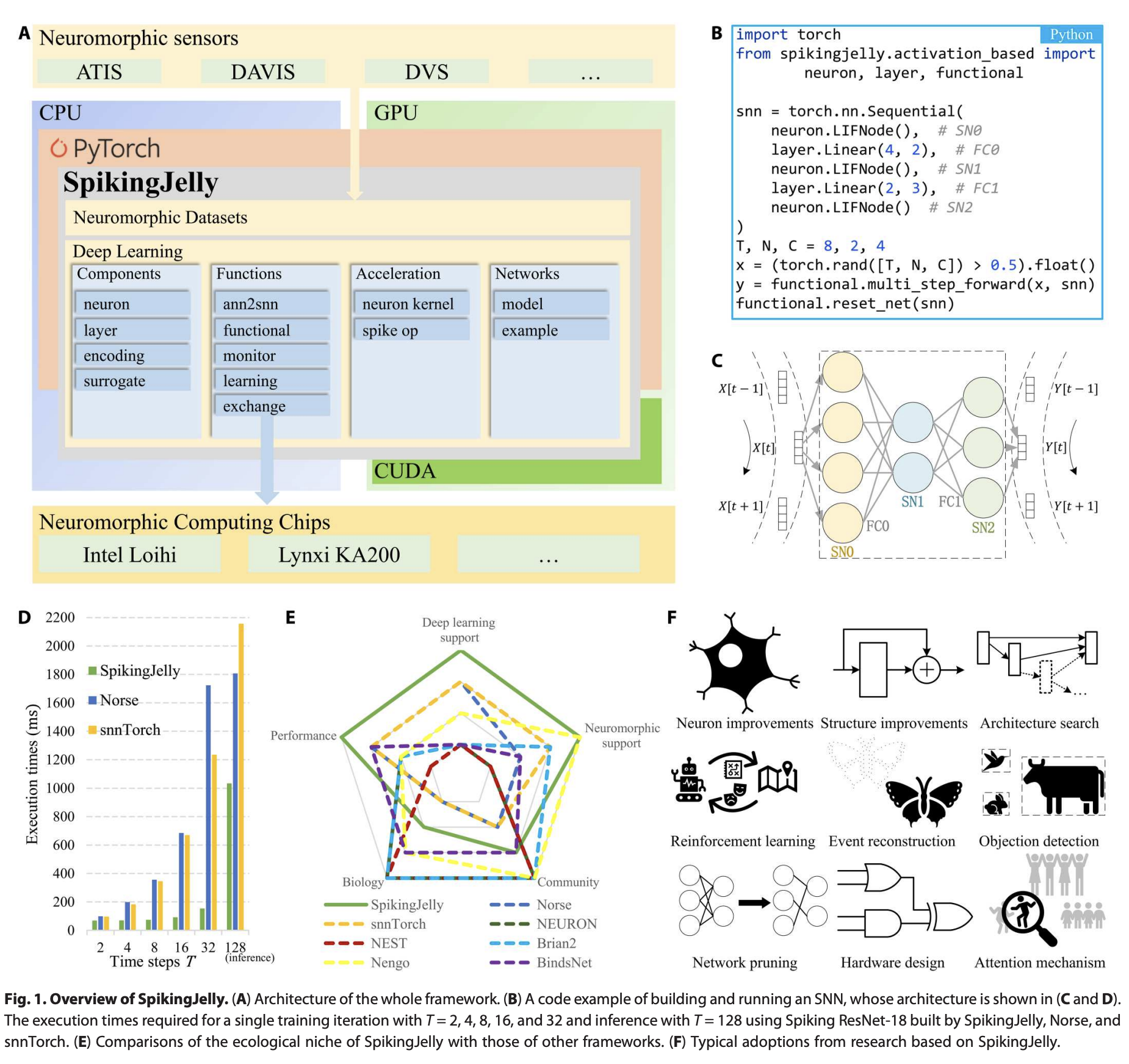
SpikingJelly惊蛰的概要如上图A，基于PyTorch，提供了SNN的全栈工具，从Neuron的定义、数据集，到使用CUDA加速训练和推理SNN，再到将SNN部署到硬件上。

Result

Convenient and flexible SNN construction

见Fig1B, 1C。提供的接口和torch的接口差不多。注意如果在多batch上做推理，每次推理新batch之前需要reset_net，要清零neuron的状态。

High-performance simulation

底层使用CUDA加速，比传统方法快。Spiking ResNet-18使用替代梯度进行训练和使用ANN2SNN的方法在惊蛰上都比之前的框架更快，且T越大加速越快。inference的速度也有较大提升，见FigD。

通过时间反向传播（BPTT）的替代梯度方法直接训练SNNs。由于内存消耗大致与时间步数T成正比，直接训练通常使用较少的时间步长；例如，对于高分辨率数据集，T ≤ 32，对于小尺寸数据集，T ≤ 64。第二种方法是使用ANN2SNN获得的权重运行SNNs。ANN2SNN评估仅限于推理，因为这一过程不需要训练。大多数ANN2SNN方法基于速率编码，需要更多的时间步长，例如，T ≥ 128。基于延迟编码而非速率编码的转换方法也有报道。需要注意的是，最近的研究已经显著减少了T，例如替代学习方法的T = 5和ANN2SNN方法的T ≤ 64。我们的评估涉及两步最常见的使用情况：（i）使用较小的时间步长进行替代学习训练，（ii）使用较大时间步长进行ANN2SNN推理。

Neuromorphic device support

要支持完整的神经模态设备的部署，首先要支持对数据输入编码成洗漱的spike的形式。

SpikingJelly提供了基于事件和基于降采样帧的两种数据集表示。事件表示与地址事件表示（AER）格式相同，这也是默认的神经形态芯片间通信协议。第 $i$ 个事件表示为 $E[i] = (x_i, y_i, t_i, p_i)$ ，其中 $(x_i, y_i)$ 是坐标， $t_i$ 是时间戳， $p_i$ 是极性。帧表示被广泛使用，并且通常是从事件表示中按时间降采样得到的。帧F是一个包含事件计数的4D张量，形状为 $(T, C, H, W)$ ，其中 $T$ 是帧的数量， $C$ 是通道数， $H$ 和 $W$ 分别是帧的高度和宽度。SpikingJelly还提供了常用的事件到帧的降采样方法。

在神经模态设备上的权重映射等似乎是单独实现的，目前支持Intel Loihi和Lynxi KA200。

Ecological niche

各种具有独特功能和特定优势的SNN框架可用，我们将其称为框架的生态位。为了说明SpikingJelly在其他框架中的独特生态位，我们总结了常用SNN框架的特点。一般来说，框架可以分为三类。

第一类包含经典的生物框架，包括NEURON、NEST和Brian2，它们使用生物神经元模型的最低级抽象，并集成（或不集成但易于实现）生物学上合理的学习规则，如STDP。为了支持GPU，一些经典框架提供了子框架，例如NEURON的CoreNEURON和Brian2的Brian2GENN，以加速从父框架派生的部分模块。Brian2还提供了Brian2-Loihi以支持Loihi芯片。随着近几十年的快速发展，经典框架已被神经科学家广泛使用，并形成了一个庞大而活跃的研究社区。

第二类可以看作是神经科学和计算机科学的交集，包括Nengo和BindsNET。这些框架采用NumPy风格设计，使用复杂度适中的神经元模型，计算成本低于经典框架。这些框架更兼容GPU，因为它们提供了GPU支持的后端，如OpenCL，或者直接基于完全支持GPU的现代机器学习框架实现。具体而言，Nengo使用基于OpenCL的NengoOCL或基于TensorFlow的NengoDL来使用GPU，BindsNET则基于PyTorch。此外，Nengo支持Loihi，这是通过NengoLoihi子框架实现的。这些框架的主要训练算法是生物学上合理的规则。需要注意的是，Nengo还通过NengoDL子框架支持ANN2SNN。Nengo丰富的生态系统使其成为最常用的框架之一。此外，新兴的BindsNET在GitHub社区吸引了数千名追随者。

第三类考虑了神经科学和深度学习的交集，包括Norse、snnTorch和SpikingJelly。所有这些框架都基于PyTorch，支持GPU和自动微分。使用高级神经元模型抽象，使这些框架能够轻松与反向传播协同工作。这些框架至少支持一种深度学习方法。由于近年来对脉冲深度学习的兴趣不断增加，这些框架受到了研究社区的高度关注。与其他框架相比，SpikingJelly具有全栈集成的优势，支持神经形态数据集和芯片、ANN2SNN和替代梯度，以及生物学上合理的学习规则，并通过针对基于尖峰的操作的特定优化技术最大化其模拟效率。

为了清晰展示，我们从五个方面比较了可用的SNN框架：模拟性能（Performance）、对神经形态传感器和计算芯片的支持（Neuromorphic Support）、社区规模（Community）、生物学抽象水平（Biology）以及对替代学习和ANN2SNN的支持（Deep Learning Support）。结果如图1E所示，展示了SpikingJelly的生态位。

Adoptions by the community

社区采纳的增加是一个框架成功的标志。自2019年12月开源以来，SpikingJelly已广泛用于许多脉冲深度学习研究中，包括对抗攻击、ANN2SNN、注意机制、基于DVS数据的深度估计、创新材料开发、情感识别、能量估计、基于事件的视频重建、故障诊断、硬件设计、网络结构改进、脉冲神经元改进、训练方法改进、医学诊断、网络剪枝、神经架构搜索、神经形态数据增强、自然语言处理、DVS/帧数据的对象检测/跟踪、气味识别、基于DVS数据的光流估计、控制的强化学习和语义通信。图1F展示了这些采纳的部分。社区的广泛采纳标志着SpikingJelly的成功。

Core modules of SpikingJelly

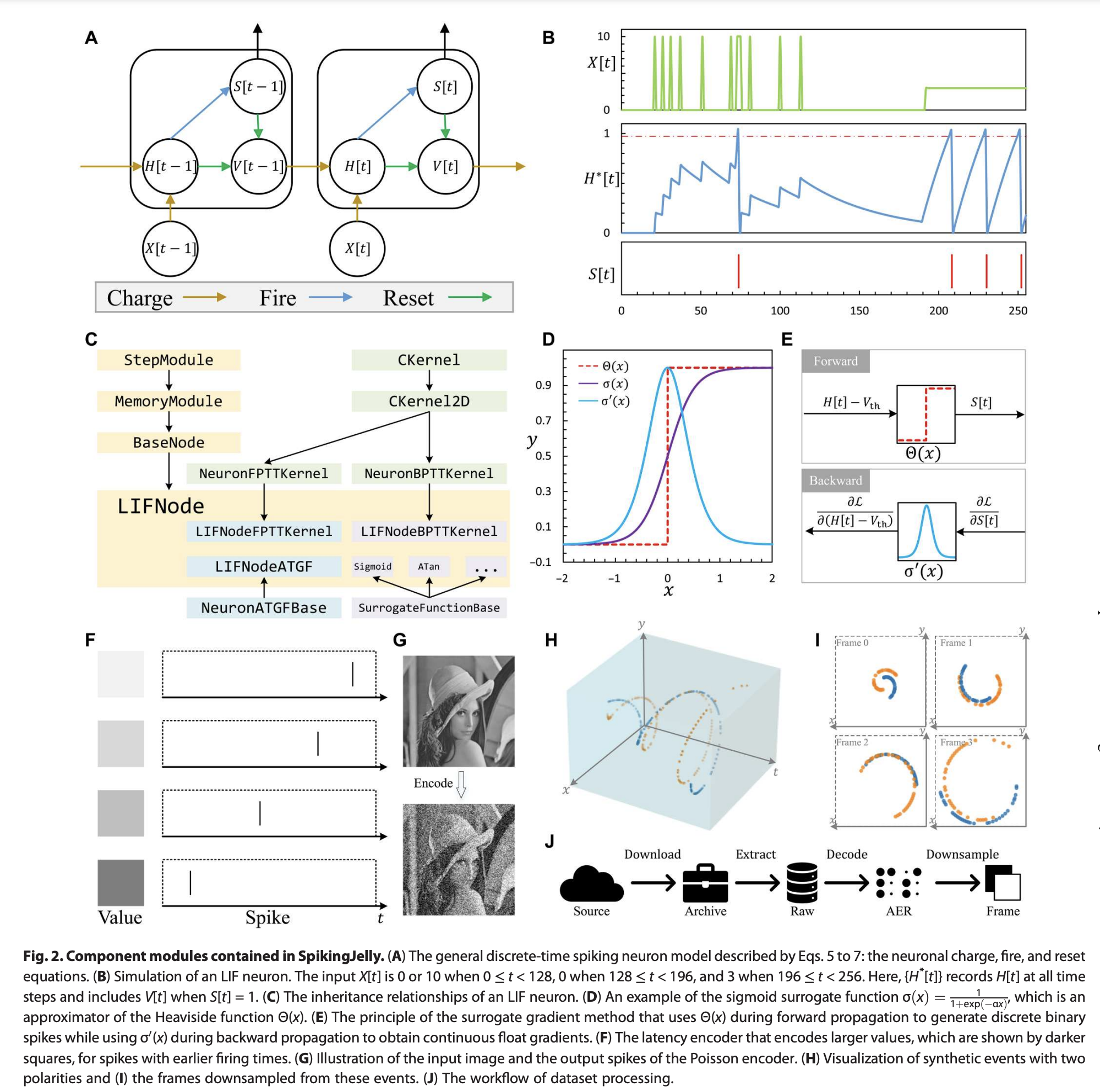
A：SpikingJelly使用三个离散时间方程，即充电、发射和复位方程，来描述脉冲神经元的行为。 $X[t]$ 、 $H[t]$ 、 $S[t]$ 和 $V[t]$ 分别是时间步 $t$ 的输入、充电后的膜电位、脉冲和复位后的膜电位。
B：在给定刺激下SpikingJelly中的LIF神经元的响应。
C：LIF神经元类的继承关系。通过继承父类，LIF神经元可以用几行代码轻松实现。
D：脉冲神经元的关键属性，包括Heaviside函数 $\Theta(x)$ 、Sigmoid替代函数 $\sigma(x) = \frac{1}{(1+exp(-\alpha x))}$ （其中 $\alpha$ 是控制形状的超参数）和替代梯度 $\sigma’(x)$ 。
E：SpikingJelly中实现替代学习的方法。 $\Theta(x)$ 在前向传播过程中用于生成脉冲，而 $\sigma'(x)$ 在反向传播过程中用于计算梯度。
F&G：SpikingJelly中的两种典型脉冲编码器，Latency encoder和Poisson encoder。
H：具有两极性的合成事件，
I：SpikingJelly降采样后的帧。
J：SpikingJelly中处理数据集的工作流程。

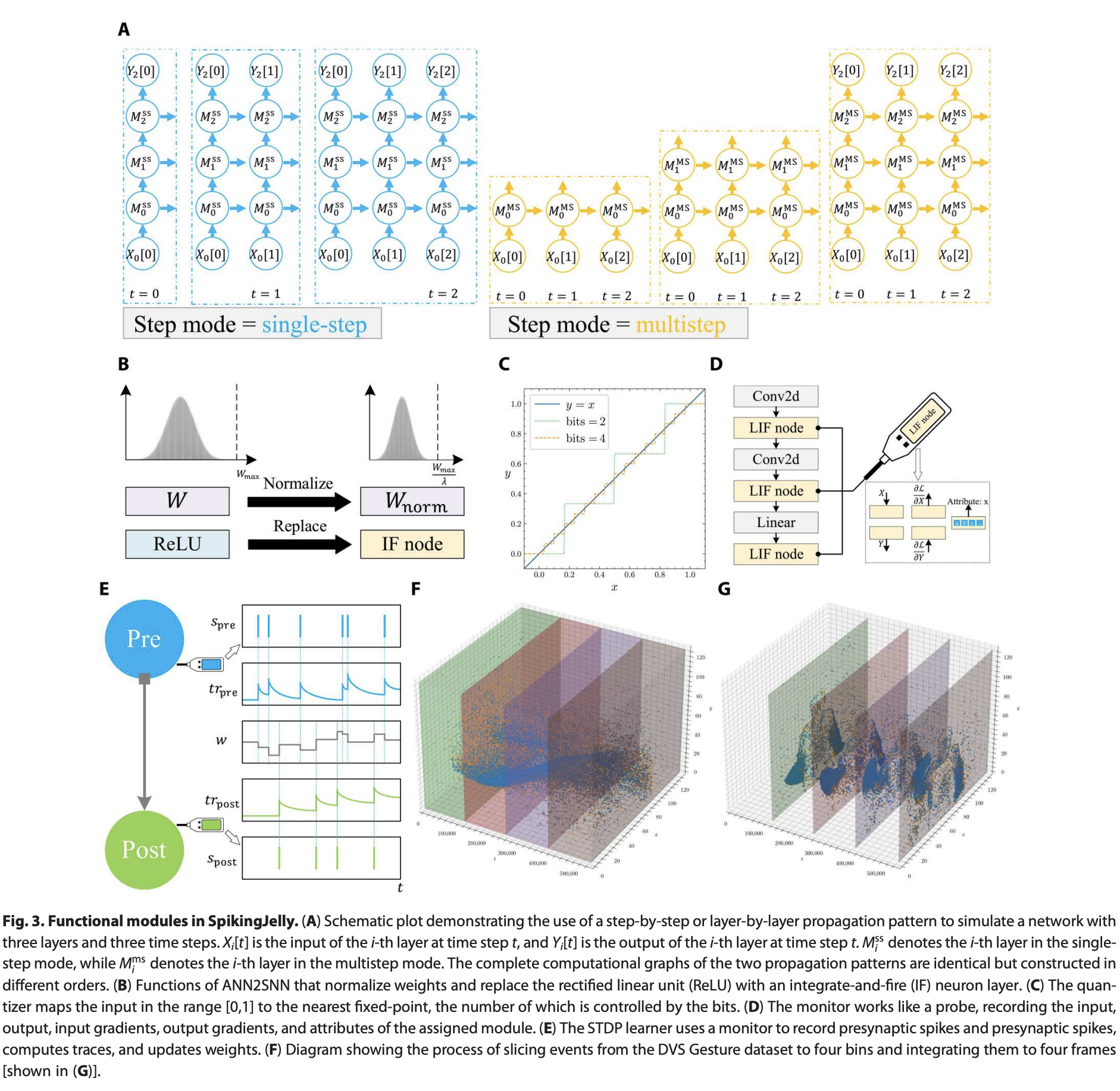
A：单步模式下，模型输入 $X[t]$ 输出 $Y[t]$ ；多步模式下模型输入 $X[t,...,t+n]$ 输出 $Y[t,...,t+n]$ 。相应地，所有模块均处于单步或多步模式的SNN分别遵循逐步或逐层传播模式，如图3A所示。这些传播模式的区别在于计算图的构建顺序。具体来说，逐步传播模式是深度优先搜索（DFS），而逐层模式是广度优先搜索（BFS）。
B：ANN2SNN，使用IF Node替换Relu。
C： $k=2$ 和 $4$ 的 $k$ 位量化器，它将输入 $x\in(0,1)$ 量化为最近的定点值 $y$ 。量化器支持QAT，在训练期间量化权重。需要注意的是，量化器的梯度几乎在所有地方都是零，因此使用了替代梯度方法。
D：使用监视器记录数据的示例。监视器像探针一样工作，从规定的模块收集数据。输入、输出、输入梯度、输出梯度和属性可以记录以满足主要的数据收集需求。
E：基于追踪方法的STDP学习器，该方法使用两个监视器记录突触前后脉冲。然后更新追踪并修改突触的权重。
F&G：事件切片和降采样操作。F中，DVS Gesture数据集的样本被切分为四个区块，这些区块显示为四个不同颜色的立方体。然后，将每个立方体中的事件累积，在G中生成四帧。

Typical applications

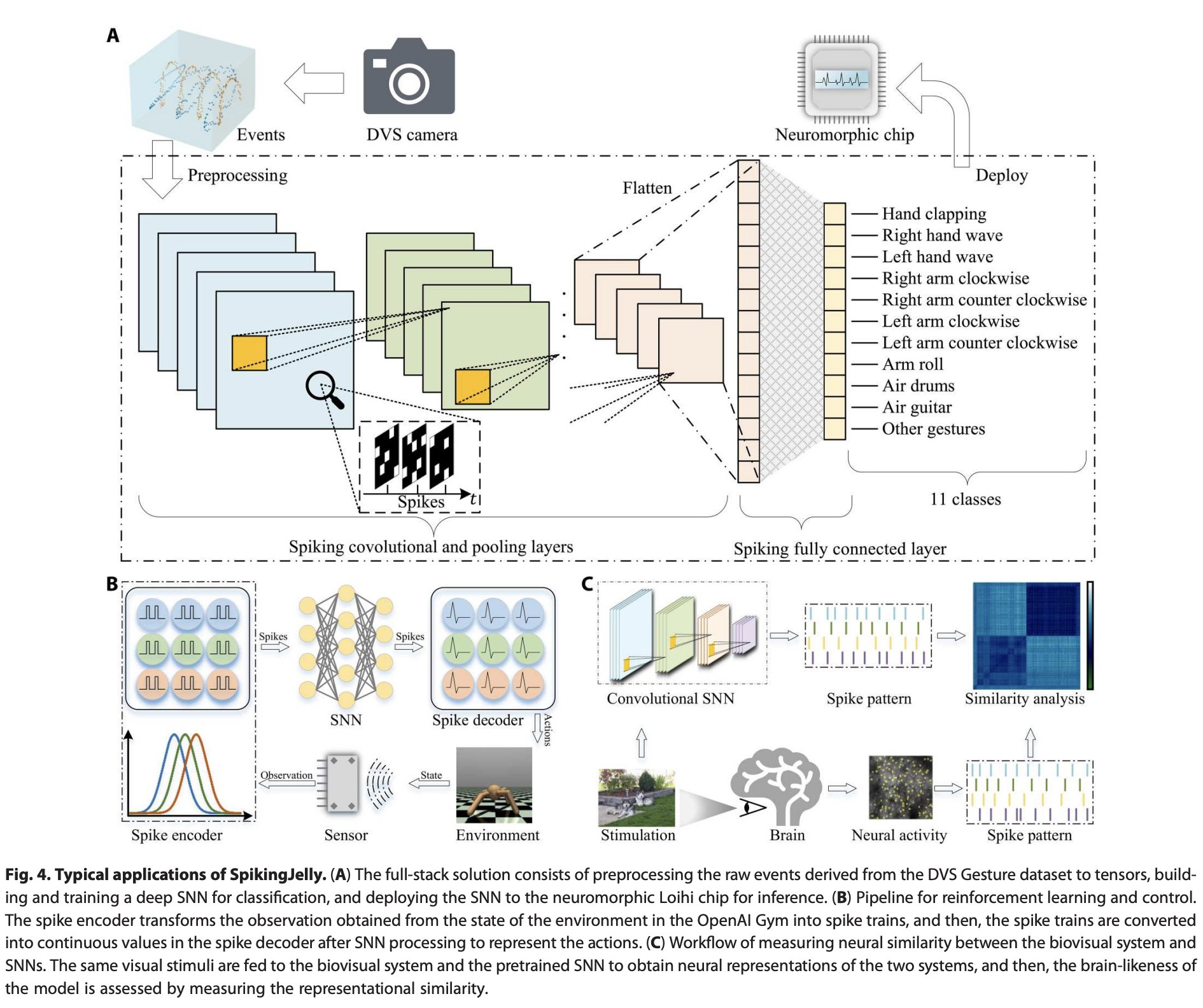
作为一个全栈工具包，SpikingJelly几乎涵盖了所有SNN应用。为了简化起见，我们在图4中展示了三个使用SpikingJelly的典型场景。

第一个案例（A）是训练一个深度SNN来分类神经形态DVS Gesture数据集的示例。首先，通过SpikingJelly的数据集子包将DVS相机的原始事件预处理为张量。然后，我们使用层、神经元和交换子包来构建和训练一个深度卷积SNN，用于分类DVS Gesture数据集。脉冲通过卷积层流动，如图4A所示。训练后，我们使用交换子包将SNN部署在神经形态Loihi芯片上进行推理。

第二个案例（B）是使用深度SNN解决来自OpenAI gym的连续控制任务的示例。首先，从环境状态中获得的观测值通过由群体神经元组成的不同高斯感受野编码，有效地将浮点值转换为脉冲列。处理后，离散的脉冲列被转换为浮点值，这些值是后续非脉冲神经元层的膜电位，以表示动作。网络中的每个模块可以通过层和神经元子包实现。

第三个案例（C）是使用深度SNN模拟生物视觉皮层的示例。首先，我们通过层和神经元子包在ImageNet分类任务上构建和训练深度SNN。然后，为了获得视觉皮层和模型的神经表征，将相同的视觉刺激输入到生物视觉系统和预训练的SNN中。最后，可以通过计算得到的表征相似性来定量分析SNN在模拟视觉皮层方面的性能。

Discussion

虽然SNNs在生物合理性和能效方面优于ANNs，但由于缺乏有效的学习方法，它们的应用主要限于神经科学领域，而非计算科学。随着深度学习方法的引入，SNNs的性能得到了极大提升，使脉冲深度学习成为新的研究热点。然而，这一新兴研究领域面临着传统软件框架侧重于神经科学而非深度学习的问题，同时新框架尚未开发。SpikingJelly旨在满足蓬勃发展的脉冲深度学习研究兴趣。

脉冲深度学习是一个新兴的跨学科领域，研究人员需要精通神经科学和深度学习。然而，专注于某一研究领域的研究人员可能对另一领域不熟悉，这与我们开发人员在回答GitHub用户问题和参与讨论时的经验一致。为减轻学习和使用成本，SpikingJelly提供了简洁方便的API。经典模型和常用的训练脚本也包括在内。即使不是熟悉底层实现的开发人员，用户也可以用几行代码轻松构建各种类型的SNNs并运行其模型。这种设计理念使用户摆脱了实现创意工作时繁琐的编码操作。

复杂多样的脉冲神经元和突触是SNNs的核心组件。通过模拟生物神经系统或参考深度ANNs的经验来修改神经元和突触是改进脉冲深度学习的可行方法。研究人员希望通过修改某些功能和属性来定义新的脉冲模块类别，并且希望只需编写少量代码即可大幅改变模型的行为和性能。SpikingJelly的灵活API支持这种研究范式。大多数SpikingJelly中的模块都是通过继承父类、覆盖函数和添加/删除新属性创建的，这也为研究人员定义新模块提供了完美的参考。

深度学习通常使用大量样本和大规模模型的数据集，还需要较多的训练周期来实现更好的性能。所有这些特征都需要大量计算资源，脉冲深度学习也是如此。此外，由于额外的时间维度，深度SNNs的计算复杂度比深度ANNs更高。因此，深度SNNs的模拟效率至关重要，特别是最近研究进展中，在包含128万张图像的ImageNet数据集上评估超过50层的深度SNNs已成为一个广泛使用的性能基准。SpikingJelly在设计时强调了计算效率。SpikingJelly的模拟过程受益于其基础设施PyTorch，它通过OpenMP/MKL实现CPU加速，通过cuBLAS/cuDNN实现GPU加速。通过融合操作引入高级加速，包括合并维度、半自动生成的CUDA内核和即时（JIT）编译，从而带来了极高的训练/推理效率。借助这些加速方法，SpikingJelly实现了最先进的模拟速度，使研究人员不再浪费大量时间等待冗长的深度SNN训练过程。

深度学习方法提高了SNNs的性能，使SNNs在实际任务中得以应用。通过SpikingJelly提供的全栈解决方案来构建、训练和部署SNNs，深度SNNs的应用范围从玩具数据集分类扩展到具有实际效用的应用，包括人类级别性能的分类、网络部署和事件数据处理。除了经典的机器学习任务外，还报告了一些深度SNNs的前沿应用，包括由可校准人工感官神经元组成的基于尖峰的神经形态感知系统、运行在忆阻器上的神经形态计算模型和设计基于事件驱动的SNN硬件加速器。所有这些证据表明，SpikingJelly的问世将加速脉冲深度学习社区的繁荣。SpikingJelly的未来发展计划将跟踪神经形态计算的进展，并见证SpikingJelly与社区的快速共生发展。

MATERIALS AND METHODS

Component modules

Neuron model

脉冲神经元是SNNs的关键组件。神经科学家更喜欢使用具有复杂神经动力学的脉冲神经元，例如Hodgkin-Huxley模型和Izhikevich模型，以实现高生物合理性。在SNNs中应用深度学习时，通常使用简化的脉冲神经元模型，包括IF和LIF模型，因为它们具有简单的神经动力学和紧凑的超参数，减少了研究人员在微调网络训练过程中的计算复杂性和工作量。

LIF Neuron:

\tau_m\frac{dV(t)}{dt}=-(V[t]-V_{rest})+X(t)

$\tau_m$ 是膜时间常数， $V(t)$ 是时间 $t$ 时的膜电位， $V_{rest}$ 是静息电位， $X(t)$ 是输入电流。当膜电位 $V(t)$ 超过阈值 $V_{th}$ 时，脉冲神经元发射脉冲 $S(t)=1$ ，否则保持沉默 $S(t)=0$ ，这可以描述为： $S(t) = \Theta(V[t] - V_{th})$ 。

如果神经元发射脉冲，则会复位。有两种复位类型：硬复位和软复位。硬复位就是将电位置为 $V_{reset}$ ，软复位则是将电位减去 $V_{th}$ ，记作：

\lim_{\Delta t\rightarrow 0^+}V(t+\Delta t)=\left\{\begin{aligned}&V_{reset}\\&V(t)-V_{th}\end{aligned}\right.

\tau_m (V[t] - V[t-1]) = -(V[t-1] - V_{rest}) + X[t]

惊蛰用下面三个方程描述Neuron：

H[t] = f(V[t-1], X[t])\\ S[t] = \Theta(H[t] - V_{th}) \\ V[t] = \begin{cases} H[t] (1 - S[t]) + V_{reset} S[t] & \text{硬复位} \\ H[t] - V_{th} S[t] & \text{软复位} \end{cases}

为了避免混淆，我们使用 $H[t]$ 表示充电后的膜电位，但在发射前，使用 $V[t]$ 表示复位后的膜电位。 $H(t)$ 是神经元充电方程， $f$ 是特定于某一神经元的函数； $S(t)$ 是神经元发射方程， $V(t)$ 是神经元复位方程。图2A展示了由这三个方程描述的一般离散时间神经元模型。

除了原始的PyTorch实现，SpikingJelly还提供了额外的可选CUDA内核来加速脉冲神经元。前向CUDA内核LIFNodeFPTTKernel、反向CUDA内核LIFNodeBPTTKernel、自适应梯度函数LIFNodeATGF和LIF神经元的替代函数也通过多级继承扩展，仅需几行代码更改。这种模块设计范式增强了SpikingJelly的扩展性，减少了研究人员开发新模型所需的工作量。当研究人员希望定义新类型的模块时，他们只需继承相应的基类并完成或重写某些函数。

Surrogate gradients

Spiking的阶跃函数无法求导，一般用 $\sigma$ 函数

\sigma(x) = \frac{1}{1 + \exp(-\alpha x)}

\frac{\partial L}{\partial (H[t] - V_{th})} = \frac{\partial L}{\partial S[t]} \cdot \sigma{\prime}(H[t] - V_{th})

求梯度。其中 $L$ 是损失函数。

Encoding

延迟编码：

S[t] = \begin{cases}1 & t = t_f \\0 & t \neq t_f\end{cases} \\t_f = [(T_{max} - 1) \cdot (1 - x)]

其中 $S[t]$ 是时间步的输出脉冲， $t_f$ 是发射时间步， $[\cdot]$ 是四舍五入函数， $T_{max}$ 是最新的发射时间步， $x$ 是输入值。延迟编码器将较大的 $x$ 编码为较早的发射时间步 $t_f$ ，表明较大的刺激应该引起更快的响应，如在视网膜路径中观察到的那样。

泊松编码：

P\left(\sum_{t=0}^{T-1} s[t] = k\right) = Pr(X = k) = \frac{(Tx)^k \exp(-Tx)}{k!}, \quad k \in \{0, 1, \dots, T\}

为了简化，实现了近似公式，如下所示：

P(S[t] = 1) = x

Neuromorphic datasets

pikingJelly提供了常用的数据集，包括ASL-DVS、CIFAR10-DVS、DVS Gesture、ES-ImageNet、HARDVS、N-Caltech101、N-MNIST、Nav Gesture和Spiking Heidelberg Digits。可以通过继承数据集基类并完成一些处理函数，轻松集成新数据集。

图2H可视化了用蓝色和绿色表示的双极性事件系列。从传感器收集的原始数据以特定格式存储，例如AEDAT，需要特定的二进制解码方法。为了降低使用成本，SpikingJelly实现了不同数据集的解码方法。相应地，SpikingJelly的数据集输出为NumPy格式，与所有Python应用程序兼容。一个样本中的事件数量可能达到数百万，网络无法直接处理。广泛使用的子采样方法将事件集成到帧中。图2I展示了从图2H中的事件集成的四个帧。SpikingJelly还提供了常用的集成方法。

图2J展示了SpikingJelly中数据集的处理流程，包括从源下载、解压归档、将原始数据解码为NumPy格式的AER Python字典，并将事件降采样为帧。用户只需继承基类并实现“下载”、“解压”和“解码”函数，其余工作由基类加速多线程处理，这也显示了SpikingJelly的优越扩展性。

Functional modules

Step modes and propagation patterns

Step By Step

Require: an SNN stacked by L single-step modules
{M_ss0, M_ss1, ..., M_ss(L-1)}, the input sequence for the 0-th layer X0 =
{X0[0], X0[1], ..., X0[T−1]}.

Create an empty list YL−1 = {}

for t ← 0,1, ..., T−1
    for l ← 0,1, ..., L−1
        X_(l+1)[t] = Y_l[t] = M_ss(l)(X_l[t])
    Append YL−1[t] in YL−1 = {YL−1[0], YL−1[1], ..., YL−1[t−1]}

Output YL−1 = {YL−1[0], YL−1[1], ..., YL−1[T−1]}

Layer By Layer

Require: an SNN stacked by L multistep modules
{M_ms0, M_ms1, ..., M_ms(L-1)}, the input sequence for the 0-th layer X0 =
{X0[0], X0[1], ..., X0[T−1]}.

for l ← 0,1, ..., L−1
    X_(l+1) = Y_l = M_ms(l)(X_l)

Output YL−1 = {YL−1[0], YL−1[1], ..., YL−1[T−1]}

图3A展示了如何通过逐步和逐层传播模式以不同顺序构建相同的计算图。考虑到SNN的计算图中有时间步长和深度两个维度，可以发现逐步和逐层传播模式分别是遍历计算图的深度优先搜索（DFS）和广度优先搜索（BFS）过程。通过更改SpikingJelly中每层的step_mode属性，可以轻松在两种传播模式之间切换。选择的传播模式由用户的意图决定。逐层模式的优势在于效率，因为时间步长上的计算可以并行执行无状态层，并且可以为有状态层实现融合操作（将在“加速模块”部分讨论）。然而，在使用逐层模式时，所有时间步长 $t$ 的输入 $X[t]$ 必须同时给出，这在 $X[t+1]$ 依赖于 $X[t]$ 时是不可能的，例如在层间使用递归连接时。在这种情况下，由于其灵活性，逐步模式是首选。

Conversion methods

转换过程基于这样的事实：在一定条件下，使用ReLU激活和平均池化的ANN与基于速率编码的SNN之间存在等价关系。基于这一事实，可以将训练好的ANN转换为相应的SNN。为了提供便捷的ANN2SNN解决方案，SpikingJelly有一个Converter模块，用于规范化ANN的权重，并通过用IF神经元层替换ReLU来将ANN转换为SNN，如图3B所示。IF Neuron的充电函数为：

H[t] = V[t-1] + X[t]

该函数没有衰减，可以通过发放率近似ANN中的ReLU。SpikingJelly中的实现基于突触后电位的建模，使得平均突触后电位等于原始ANN的激活值。我们提供一个VoltageHook模块，用于记录隐藏特征的最大值（或某个百分位值）作为转换后的SNN的突触后电流的尺度。然后，激活值通过IF神经元层改变以完成转换过程。此外，为了快速推理（即使用较少时间步长进行推理），我们在SpikingJelly中提供了即插即用的优化膜电位初始化。

Quantizer

为了在资源受限的硬件上（包括现场可编程门阵列、神经形态芯片和移动电话）进行SNN推理，网络量化是一种必要的技术，可以减少存储和计算成本。例如，与32位模型相比，量化到8位的网络在模型大小和内存带宽要求方面减少了4倍，吞吐量提高了多达4倍。SpikingJelly提供了一个量化器，用于量化感知训练，可以在训练期间量化权重和神经元动力学。图3C展示了SpikingJelly中的一个典型的k位量化器，它将范围 $[0,1]$ 内的输入 x 映射到最近的定点值 y = $q(x) = \frac{[\{(2^k - 1)x\}]}{2^k - 1}$ ，其中 $[·]$ 是四舍五入函数。需要注意的是， $q{\prime}(x)$ 几乎在所有地方都是零，因此SpikingJelly也使用替代方法重新定义其梯度。

Monitor

研究人员经常需要记录数据，例如脉冲神经元层的发放率。为了满足记录数据的需求，SpikingJelly提供了五个通用监视器，可以在前向/后向传播过程中监控输入/输出以及特定层的属性。如图3D所示，监视器像探针一样工作，插入用户定义类型的层，并通过自定义变换λ记录数据。例如，如果我们对SNN中所有脉冲神经元的发火率感兴趣，可以将OutputMonitor设置为脉冲神经元层的层类型，并将自定义变换设置为 $\lambda(S) = \frac{1}{T} \sum_{t=0}^{T-1} S[t]$ ，其中T是时间步数， $S[t]$ 是时间步 $t$ 的脉冲。使用这个监视器，我们可以轻松记录每个脉冲神经元的发放率。

STDP Learner

将局部无监督的 STDP 学习过程与全局监督的替代梯度结合，已成为深度SNN的一种有前景的学习方法，这可以通过 SpikingJelly 中的 STDP 学习器实现。在图 3E 所示的两个神经元的最小示例中，SpikingJelly 中的 STDP 学习器使用了基于追踪方法的“全对全”STDP，其中考虑了所有突触前和突触后脉冲对。它使用监视器记录突触前脉冲 $s_{\text{pre}}$ 和突触后脉冲 $s_{\text{post}}$ 。然后，追踪 $\text{tr}_{\text{pre}}[t]$ 和 $\text{tr}_{\text{post}}[t]$ 更新为：

\text{tr}_{\text{pre}}[t] = \text{tr}_{\text{pre}}[t-1] - \frac{\text{tr}_{\text{pre}}[t-1]}{\tau_{\text{pre}}} + s_{\text{pre}}[t]\\ \text{tr}_{\text{post}}[t] = \text{tr}_{\text{post}}[t-1] - \frac{\text{tr}_{\text{post}}[t-1]}{\tau_{\text{post}}} + s_{\text{post}}[t]

其中， $\tau_{\text{pre}}$ 和 $\tau_{\text{post}}$ 分别是突触前和突触后的时间常数。然后，权重 $w$ 根据追踪进行更新：

\Delta w[t] = F_{\text{post}}(w[t]) \cdot \text{tr}_{\text{pre}}[t] \cdot s_{\text{post}}[t] - F_{\text{pre}}(w[t]) \cdot \text{tr}_{\text{post}}[t] \cdot s_{\text{pre}}[t]

其中， $F_{\text{pre}}$ 和 $F_{\text{post}}$ 是用户自定义的函数，用于控制突触变化的幅度。在 SpikingJelly 中， $\Delta w$ 可以加到梯度 $\frac{\partial L}{\partial w}$ 上，这表明 STDP 学习器可以与梯度下降法和各种优化器（包括动量随机梯度下降和自适应矩估计（Adam））一起工作。

Event downsampling methods

固定时间段 $\Delta T$ 集成事件：

F[j; p; y; x] = \sum_{t_0 + j \cdot \Delta T \leq t_i < t_0 + (j+1) \cdot \Delta T} I_{p, y, x}(p_i, y_i, x_i)

其中， $I_{p, y, x}(p_i, y_i, x_i)$ 是指示函数，仅当 $(p, y, x) = (p_i, y_i, x_i)$ 时等于1。但是注意到，在事件相机这样的设备中，固定时间段内包含的帧数不一定相同（触发事件多少），所以也有固定帧数的降采样方法：

F[j; p; y; x] = \sum_{i = j_l}^{j_r - 1} I_{p, y, x}(p_i, y_i, x_i)

其中， $j_l$ 和 $j_r$ 是由特定分割方法创建的索引。例如，按事件数量分割如下进行：

j_l = \left\lfloor \frac{N}{T} \right\rfloor \cdot j

j_r = \left\{\begin{aligned}&\left\lfloor \frac{N}{T} \right\rfloor \cdot (j + 1)，j < T - 1\\&\quad N ,j = T - 1\end{aligned}\right.

其中， $\left\lfloor \cdot \right\rfloor$ 是取整操作， $N$ 是事件数量。按事件持续时间分割如下进行：

\Delta T = \frac{t_{N-1} - t_0}{T}

j_l = \arg \min_k \{ t_k | t_k \geq t_0 + \Delta T \cdot j \}

j_r = \left\{\begin{aligned}&\arg \min_k \{ t_k | t_k < t_0 + \Delta T \cdot (j + 1) \} + 1, \quad j < T - 1\\& N,\quad j = T - 1\end{aligned}\right.

需要注意的是，基于固定帧数的集成只有在所有事件到达后才能使用，这使得它不适用于事件持续时间不可预测的实时系统。SpikingJelly 还支持用户自定义的切片和集成方法，它们实现为可调用函数，并在初始化参数中使用。

Acceleration modules

Principle of acceleration

SpikingJelly 通过两种方法加速 SNNs 的模拟：无状态层的并行计算和有状态层的 CUDA 内核融合。这两种方法分别针对不同类型的层，优化它们的计算效率。

无状态层的并行计算

无状态层（例如卷积层和线性层）在 SNN 中广泛使用。这些层接收形状为 $(T, N, …)$ 的输入序列 $X = \{X[0], X[1], \dots, X[T-1]\}$ 。无状态层的一个重要特点是它们在时间步长之间没有依赖关系，即 $Y[t]$ 的计算仅依赖于 $X[t]$ 。因此，我们可以并行处理这些时间步长，而不需要使用 for 循环。

为此，SpikingJelly 提供了 SeqToANNContainer 或其功能性公式 seq_to_ann_forward 来包装无状态层或它们的前向传播。SeqToANNContainer 通过将输入张量的形状从 $(T, N, …)$ 重塑为 $(T \cdot N, …)$ ，将时间步维度合并到批处理维度中。然后，输入序列被发送到无状态层，在所有时间步长上并行执行计算。计算完成后，输出被拆分回原始的时间步序列 $Y = \{Y[0], Y[1], \dots, Y[T-1]\}$ 。

相当于，对于这些不是Neuron的层，把多个timestep当成不同的batch，然后全部丢进去处理再拆分成不同的timestep。

有状态层（Neuron）的算子融合

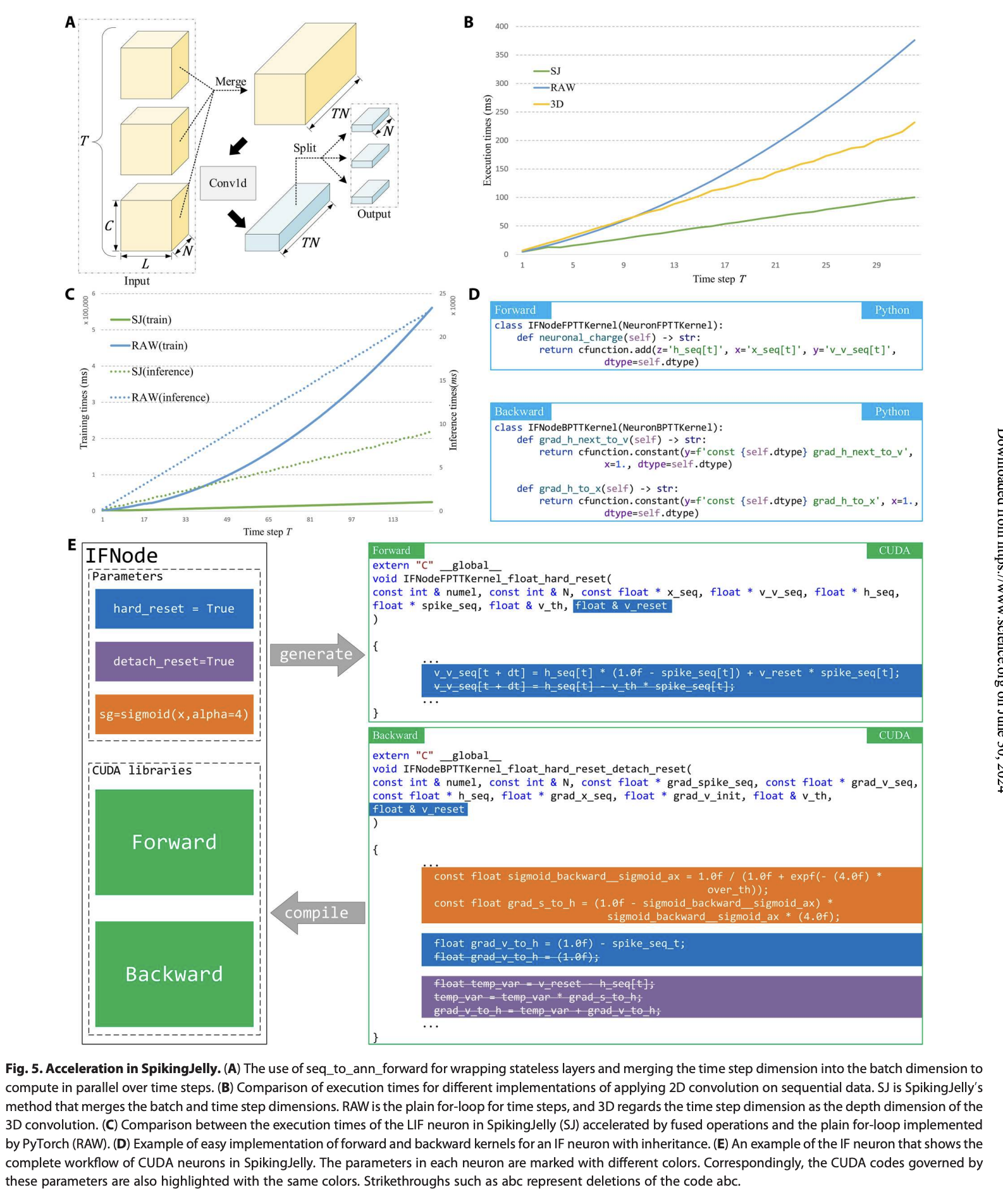
对于有状态层如脉冲神经元， $Y[t]$ 不仅依赖于 $X[t]$ ，还依赖于隐藏状态 $H[t-1]$ ，而后者依次依赖于 $X[t-1]$ 、 $X[t-2]$ 等。因此，时间步长的 for 循环是不可避免的。然而，当使用 PyTorch 实现的简单 for 循环时，在每个时间步长都会调用一个或一系列 CUDA 内核。频繁调用许多小的 CUDA 内核会浪费时间在调用开销上，包括内存访问时间和内核启动时间，从而降低网络的计算效率。为了加速有状态层，SpikingJelly 将许多小内核融合为几个大内核，从而避免调用开销。图 5C 比较了通过 CUDA 内核融合方法（SJ）和 PyTorch 实现的简单 for 循环（RAW）在多步模式下实现的 LIF 神经元的训练和推理过程的执行时间。结果显示，SJ 比 RAW 快得多。还可以发现，随着 (T) 的增加，推理过程中的执行时间都呈线性增长。然而，训练过程中 RAW 的执行时间呈二次增长，而 SJ 的执行时间随着 (T) 的增加仍然增长缓慢。有关 SpikingJelly 中加速方法效果的更多细节，请参见补充材料中的“加速方法的消融研究”部分。

Semiautomatic CUDA code generation

为了简化开发过程，SpikingJelly 使用 CuPy 实现 CUDA 内核。在 Python 字符串中定义一个原始 CUDA 内核后，CuPy 包装并编译该字符串以生成 CUDA 二进制库，该库在后续运行中被缓存和重用。引入 CuPy 避免了 CUDA、C++ 和 Python 之间的绑定琐事，并帮助用户专注于纯 Python 开发环境。使用 CuPy 的显著优势在于 CUDA 代码编写在 Python 字符串中，这意味着我们可以在 Python 环境中轻松控制 CUDA 代码。结合 SpikingJelly 的优越扩展性，这一特性大大简化了创建 CUDA 内核的过程。如图 2C 所述，特定神经元类的前向内核和后向内核从神经元内核基类扩展，代码更改量相对较小（参见补充材料中的“神经元内核详细信息”部分）。根据前向传播的方程，后向传播过程定义为：

\frac{dL}{dH[t]} = \frac{\partial L}{\partial S[t]} \frac{dS[t]}{dH[t]} + \frac{\partial L}{\partial V[t]} + \frac{dL}{dH[t+1]} \frac{dH[t+1]}{dV[t]} \frac{dV[t]}{dH[t]}

\frac{dL}{dX[t]} = \frac{dL}{dH[t]} \frac{dH[t]}{dX[t]}

其中 $\frac{dS[t]}{dH[t]}$ 由替代函数定义， $\frac{dH[t+1]}{dV[t]}$ 和 $\frac{dH[t]}{dX[t]}$ 由前面的Neuron定义的相关方程定义，而其他部分对不同类型的神经元是通用的。因此，SpikingJelly 中的神经元内核基类是一个不完整的 CUDA 内核，包含继承者需要完成的空函数，包括前向传播过程的方程和后向传播过程的 $\frac{dH[t+1]}{dV[t]}$ 和 $\frac{dH[t]}{dX[t]}$ 。例如，当我们使用 IF 神经元时，其神经元充电函数和后向传播过程定义为：

H[t] = V[t-1] + X[t]

\frac{dH[t+1]}{dV[t]} = 1

\frac{dH[t+1]}{dV[t]} = 1

然后，IFNodeFPTTKernel 和 IFNodeBPTTKernel 的前向传播通过时间 (FPTT) 内核和后向传播通过时间 (BPTT) 内核如图 5D 所示。FPTT 内核在单个 CUDA 内核中实现了包括方程（12）、（6）和（7）在内的 IF 神经元的神经动力学在 T 个时间步长中的前向传播。相应地，BPTT 内核在单个 CUDA 内核中实现了所有时间步长的神经动力学的后向传播（见算法 S3）。我们发现完成这些空函数只需要几行代码。

图 5E 展示了 SpikingJelly 中 CUDA 神经元的完整工作流程，以 IF 神经元为例。神经元中的参数用不同颜色标记。相应地，由这些参数控制的 CUDA 代码也用相同颜色高亮显示。例如，当硬复位为真时，Python 类执行以下操作，这些操作也在图5E 中用蓝色高亮显示：

（i）在前向和后向内核的参数中添加 $v_{reset}$ 。

（ii）在前向内核中保留硬复位命令 v_v_seq[t + dt] = h_seq[t] * (1.0f - spike_seq[t]) + v_reset * spike_seq[t]，并删除软复位命令 v_v_seq[t + dt] = h_seq[t] - v_th * spike_seq[t]。

（iii）在后向内核中保留后向硬复位命令 float grad_v_to_h = (1.0f) - spike_seq_t，并删除后向软复位命令 float grad_v_to_h = 1.0f。当 detach_reset为真时，方程（7）中的 $S[t]$ 从后向计算中分离出来，然后删除相应的 CUDA 代码，如图 5E 中的紫色高亮所示。用于替代学习的 CUDA 代码由替代函数类生成，如图 5E 中的橙色高亮所示。在 CUDA 代码生成过程之后，CuPy 编译这些 CUDA 代码到 CUDA 库中，前向/后向计算可以通过融合操作在大 CUDA 内核中加速。

JIT acceleration

JIT 是一种用于加速网络的替代方法，可以在运行时将 Python 代码编译为高性能的 C++/CUDA 程序。一些简单的逐元素操作，例如神经元发射和神经元复位操作，可以通过 JIT 包装到一个 CUDA 内核中。作为一种常见的优化方法，JIT 不仅性能较低，而且开发成本也低于特定的优化方法，如手动编写 CUDA 代码。因此，SpikingJelly 使用半自动生成的 CUDA 内核来处理复杂操作，例如具有梯度的脉冲神经元的时间步长前向和后向内核，并使用 JIT 加速其他简单功能，例如单个时间步长的神经元动力学。图 5C 中显示了一个典型示例，其中 SJ 的推理过程通过 JIT 加速。

工作特别全面，并且工程量特别大，现在的新的SNN的应用和不做新Neuron的工作好像都是基于惊蛰做的，因为影响力很大所以上了Science。可以关注一下CUDA层面的优化具体是怎么做的。

SpikingJelly: An open-source machine learning infrastructure platform for spike-based intelligence