摘要： 脉冲神经网络（SNNs）由于在神经形态硬件上的高能效，成为人工神经网络（ANNs）的潜在竞争者。然而，在训练过程中，SNNs 是通过时间步展开的。因此，SNNs 需要比 ANNs 更多的内存，这阻碍了更深的 SNN 模型的训练。在本文中，我们提出了可逆脉冲神经网络，以减少训练过程中中间激活和膜电位的内存消耗。首先，我们沿时间维度扩展了可逆架构，提出了可逆脉冲块，这可以通过逆向过程重构计算图并重新计算所有中间变量。在此基础上，我们将最先进的 SNN 模型采用到可逆变体，即可逆脉冲 ResNet（RevSResNet）和可逆脉冲 Transformer（RevSFormer）。通过在静态和神经形态数据集上的实验，我们证明了我们的可逆 SNNs 的每张图像的内存消耗不会随着网络深度的增加而增加。在 CIFAR10 和 CIFAR100 数据集上，我们的 RevSResNet37 和 RevSFormer-4-384 达到了可比的准确率，并比其具有大致相同模型复杂性和参数的对应模型每张图像消耗更少的 GPU 内存，分别是 3.79 倍和 3.00 倍。我们相信这项工作可以释放 SNN 训练中的内存限制，为训练超大和超深的 SNNs 铺平道路。代码可以在 https://github.com/mi804/RevSNN.git 获取。

1. Intro

BPTT在训练的过程中需要模拟时间步长T，导致训练的时候需要更高的计算资源和内存带宽。计算资源可以通过加速器弥补，但是这种巨大的显存占用导致训练的时候只能采用较小的batch size，或者直接无法训练大型的SNN。

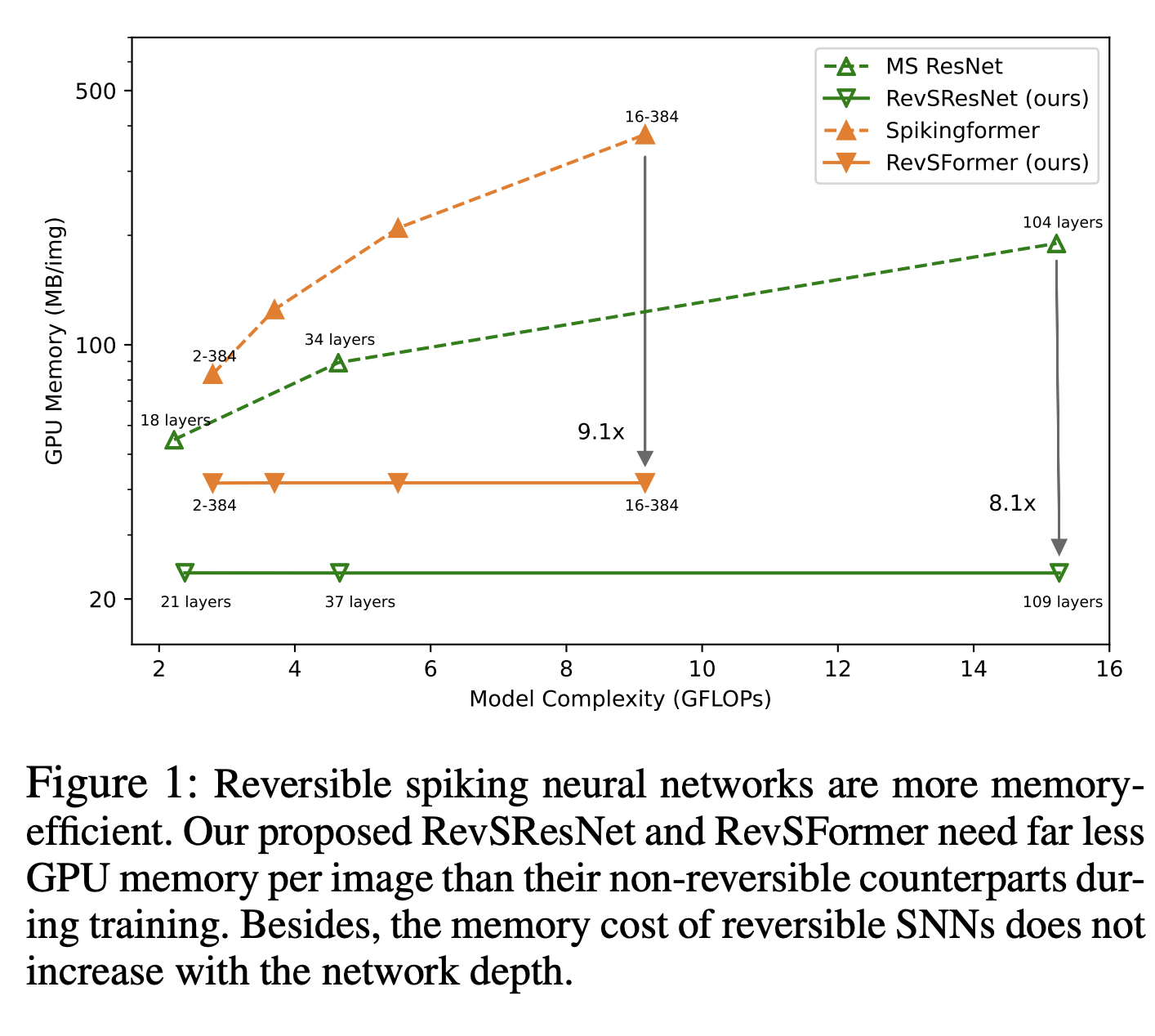
SNNs 的高内存消耗来自多个方面。一方面，与 ANNs 类似，SNNs 所需的内存随着网络深度线性增加。网络越深，所需存储的参数和中间激活就越多。另一方面，与 ANNs 不同的是，SNNs 的内存消耗还会随着模拟时间步长 T 增加。SNNs 需要存储 T 倍的中间激活，并且还需要存储脉冲神经元的膜电位以进行梯度计算。显然，大量的内存消耗来自于存储中间激活和膜电位。通过减少这部分消耗，我们可以在很大程度上解耦内存增长与网络深度的关系。

Contributions:

分析了 SNNs 在空间和时间维度上的可逆性，并为 BPTT 框架提出了脉冲可逆块。在此基础上，每个块的输入和中间变量可以通过其输出计算出来。
我们提出了可逆脉冲 ResNet（RevSResNet）和可逆脉冲 Transformer（RevSFormer）。我们重新设计了一系列结构（如下采样层、可逆脉冲残差块和可逆脉冲 Transformer 块）以匹配非可逆的最先进脉冲对应模型的性能。
实验表明，RevSResNet 和 RevSFormer 具有与其非可逆对应模型相当的性能。同时，我们的可逆模型在训练过程中显著减少了内存成本。

SNNs： 没有太多好介绍的，老几样

Reversible Architectures： 基于NICE可逆变换的神经网络：

可逆 ResNet（Gomez 等，2017）是第一个将其用于基于 CNN 的图像分类任务的工作。他们采用可逆块来完成内存高效的网络训练。其内存节省的核心在于中间激活可以通过反向过程重构。之后，其他工作（Hascoet 等，2019；Sander 等，2021；Li 和 Gao 2021）进一步迭代了基于 CNN 的可逆架构。最近，（Mangalam 等，2022）将可逆变换应用于视觉 Transformer，提出了 Rev-ViT 和 RevMViT 两种内存高效的 Transformer 结构。他们发现，可逆架构比非可逆架构具有更强的固有正则化。此外，可逆变换还被应用于其他网络，如 UNet（Brugger, Baumgartner 和 Konukoglu 2019）、掩码卷积网络（Song, Meng 和 Ermon 2019）和图神经网络（Li 等，2021a）。值得注意的是，上述可逆架构在空间维度上是可逆的，其中前向过程从浅层传播到深层，反向过程从深层传播到浅层。与它们不同的是，可逆 RNN（MacKay 等，2018）在时间维度上是可逆的。它通过从未来反转计算过去的隐藏状态。SNN 是一个具有空间和时间维度的网络，而我们的脉冲可逆块在空间维度上是可逆的，在时间维度上是一致的。

3. Approach

3.1. Spiking Neuron Model

用的还是LIF和IF，没什么好写的。

3.2. Spiking Reversible Block

3.2.1 Computation graph of spiking reversible block

在标准的反向传播训练中，单个批次通过正向-反向过程计算。相比之下，对于可逆块，这种计算变为正向-反向-反向过程。添加的反向过程利用块的输出来反向计算输入。然后，我们可以在正向过程之后删除所有输入和中间变量，只保留输出。RevNet (Gomez et al. 2017) 和 RevRNN (MacKay et al. 2018) 分别在空间和时间维度上实现了可逆块。

在_NICE: Non-linear Independent Components Estimation _ 中首次提出了这种可逆分块变换。考虑 $y=f(x)$ 这样一个变换，NICE中的coupling layer可以写作：

y_{1:d}=x_{1:d}\\y_{d+1:D}=x_{d+1:D}+m(x_{1:d})

其中 $m$ 是任意复杂函数；做逆变换的时候，有：

x_{1:d} = y_{1:d}\\x_{d+1:D}=y_{d+1:D}-m(y_{1:d})

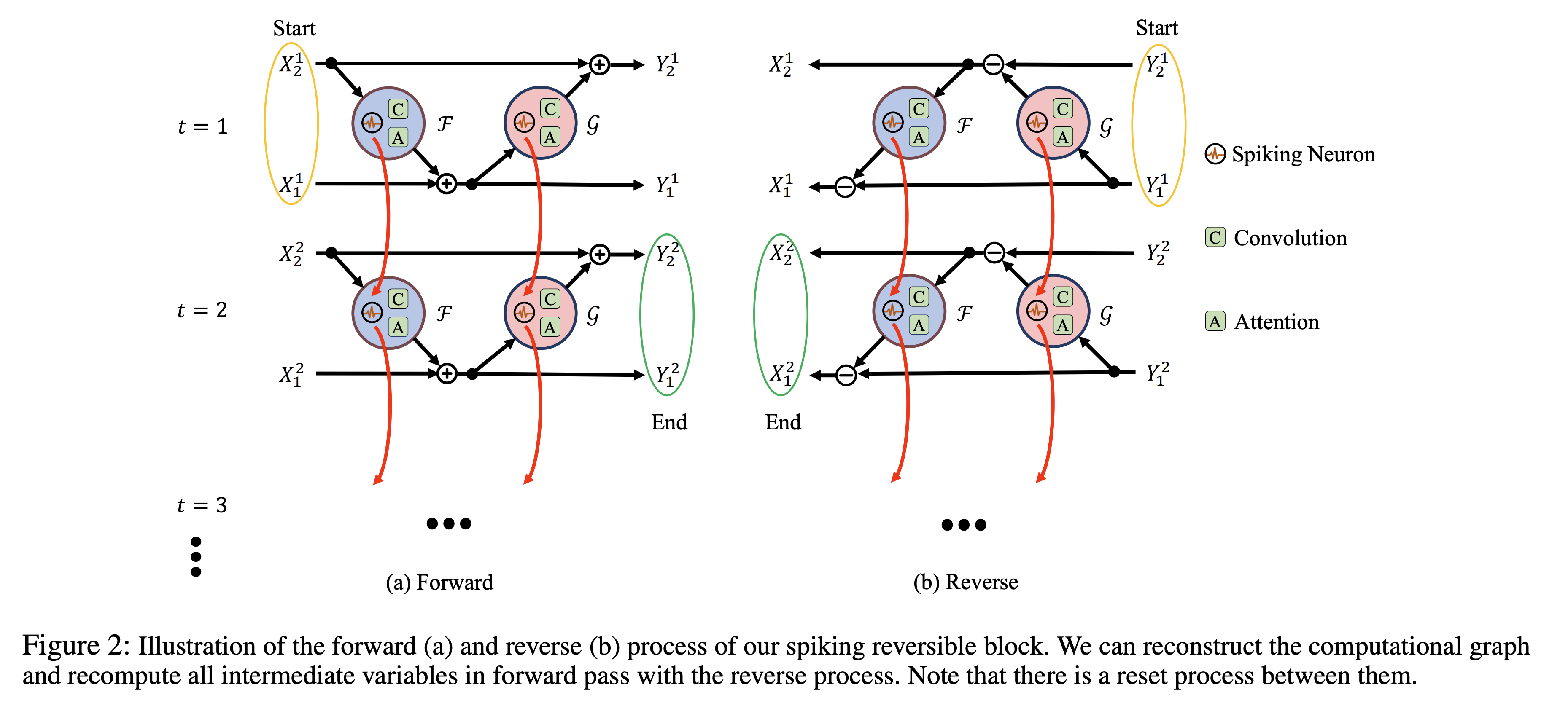
目标就是通过构建这种可逆的函数，使得在训练的过程中不需要保存中间的权重信息来计算梯度，而是使用这种逆变换求中间的状态，保证只要得到最后的输出，就可以一步一步计算出来所有中间的状态。

前向的计算过程中，计算图开始于timestep1的input，结束于timestep T的output，在每个timestep中，output $Y^T$ 通过：

Y^t_1 = X^t_1 + F^t(X^t_2) \\ Y^t_2 = X^t_2 + G^t(Y^t_1)

计算，其中的 $F, G$ 可以是任意的neuron，卷积，FC，Attention等各种函数（任意复杂函数）然后，有上标是因为neuron会随着时间发生变化。

反向计算的时候，首先要将膜电位reset，计算图开始于timestep1的output，结束于timestepT的input（在空间上可逆，而时间上一致），然后计算：

X^t_2 = Y^t_2 - G^t(Y^t_1) \\ X^t_1 = Y^t_1 - F^t(X^t_2)

3.2.2. Leaning without caching intermediate variables

考虑第 $l$ 层的neuron的权重 $W_l$ ，梯度可以写作：

\frac{\partial L}{\partial W_l} = \sum_{t} \left( \frac{\partial L}{\partial S^t_l} \frac{\partial S^t_l}{\partial U^t_l} + \frac{\partial L}{\partial U^{t+1}_l} \frac{\partial U^{t+1}_l}{\partial U^t_l} \right) \frac{\partial U^t_l}{\partial W_l}

其中 $S^t_l, U^t_l$ 是 $t$ 时刻的输出spike和膜电位。上面这个式子可以看出，需要所有timestep中的所有spike和电位。在标准训练中，这些变量在前向过程后被缓存到 GPU 内存中。由于网络的顺序性质，所有层在所有时间步的中间变量都应被存储。因此，峰值内存使用量与网络深度 $D$ 和时间步 $T$ 成线性关系。其空间复杂度为 $O(D \cdot T)$ 。

对于脉冲可逆块的训练，提出定理：

Theorem 1: 考虑一个具有 T 时间步的脉冲可逆块，如果正向和反向函数如公式 5 和公式 6 所示，并且正向过程的输出被输入到反向过程，那么在正向过程中的 $X^t$ , $Y^t$ 和所有中间变量（包括中间激活和膜电位）在 $F^t$ 和 $G^t$ 中与反向过程中的相同。

证明：

正逆向推理过程：

Y^t_{f1} = X^t_{f1} + F^t_f(X^t_{f2}) \\ Y^t_{f2} = X^t_{f2} + G^t_f(Y^t_{f1}) \\\quad\\ X^t_{r2} = Y^t_{r2} - G^t_r(Y^t_{r1}) \\ X^t_{r1} = Y^t_{r1} - F^t_r(X^t_{r2})

为方便区分，我们使用 $X^t_f, Y^t_f, F^t_f,$ 和 $G^t_f$ 来表示在时间步 $t$ 前向过程的输入、输出和脉冲模块。而 $X^t_r, Y^t_r, F^t_r,$ 和 $G^t_r$ 分别表示在时间步 t 反向过程的输入、输出和脉冲模块。我们的目标是证明在每个时间步 t 下， $X^t_f = X^t_r, F^t_f = F^t_r,$ 和 $G^t_f = G^t_r，$ 条件是 $Y^t_f = Y^t_r$ 。

由于不同过程中的脉冲模块共享相同的参数，主要的区别在于膜电位。设 $V^t_f$ 和 $V^t_r$ 分别为前向和反向过程中的膜电位。在时间步 1 时，由于所有膜电位都初始化为零，则有：

V^1_f = V^1_r = 0

因此，在时间步 1， $F^1_f = F^1_r$ 且 $G^1_f = G^1_r$ 。

由于 $Y^1_{f1} = Y^1_{r1}$ ，这些是 $G^1_f$ 和 $G^1_r$ 的输入，因此 $G^1_f$ 和 $G^1_r$ 的所有中间变量和输出相同。即：

G^1_f(Y^1_{f1}) = G^1_r(Y^1_{r1})

根据公式 8 和 9，我们可以证明 $X^1_{f2} = X^1_{r2}$ ，这些是 $F^1_f$ 和 $F^1_r$ 的输入。然后 $F^1_f$ 和 $F^1_r$ 的所有中间变量和输出相同。即：

F^1_f(X^1_{f2}) = F^1_r(X^1_{r2})

然后我们可以证明 $X^1_{f1} = X^1_{r1}$ 。

到目前为止，我们已经证明了 $X^1_f = X^1_r，F^1_f = F^1_r，$ 和 $G^1_f = G^1_r$ 。并且前向和反向过程中的膜电位更新都是相同的，这意味着：

V^2_f = V^2_r

从上述证明中，我们可以发现膜电位相等是其他变量相等的充分条件。同样，根据公式 13，我们也可以得到在时间步 2 下 $X^2_f = X^2_r，F^2_f = F^2_r，G^2_f = G^2_r，$ 和 $V^3_f = V^3_r$ 。

通过进一步推理，对于每个时间步 t，都有 $X^t_f = X^t_r，F^t_f = F^t_r，$ 和 $G^t_f = G^t_r$ 。并且前向和反向过程中的所有中间变量在 F^t 和 G^t 中是相同的。

3.3. Reversible Spiking Residual Neural Network

Basic Block：

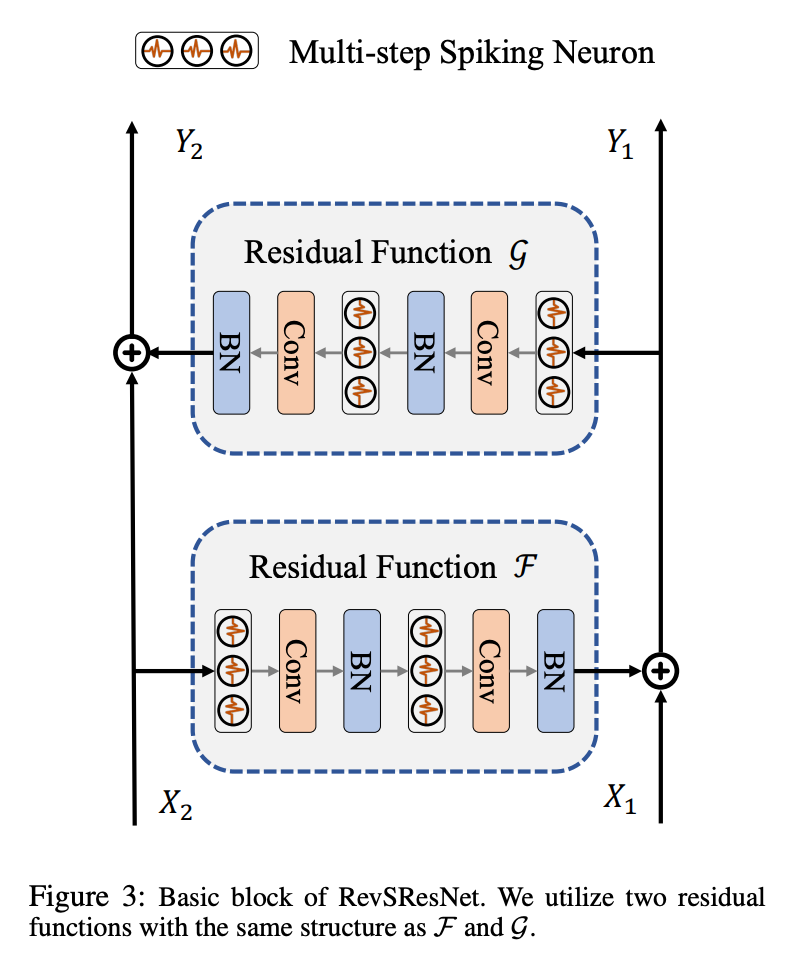
Downsample Block：

由于基本块的可逆性，X 和 Y 的特征维度是相同的。因此，残差函数 F 和 G 必须在输入和输出空间中具有相同的维度，这意味着下采样层（如最大池化或步幅为 2 的卷积）不能出现在脉冲可逆块中。为了替换 ResNet 中的下采样基本块，我们在需要下采样的阶段开始设置了一个下采样块。我们首先使用步幅为 2 的 3×3 平均池化对图像尺度进行下采样，然后使用步幅为 1 的 1×1 卷积层增加特征通道。

网络结构：

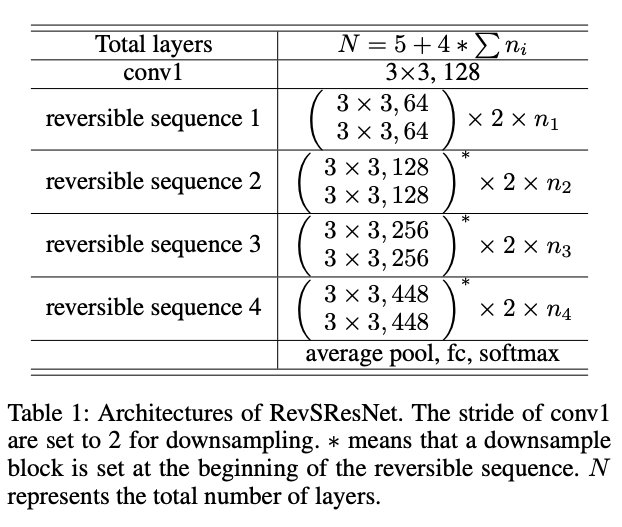
RevSResNet 的高层结构与其非可逆对应的 MS ResNet（Hu 等，2021）相同。第一个卷积层被视为编码层，执行初始下采样。然后，脉冲特征通过四个带有基本块的阶段传播。我们在第二到第四阶段的开始设置了一个下采样块。网络以平均池化和全连接层结束。当脉冲可逆块按顺序连接时（我们称之为可逆序列），我们只需要存储最后一个块的输出来完成训练。除去下采样块，RevSResNet 中的所有阶段都是可逆序列。无论可逆序列中块的数量如何增加，中间变量所需的内存使用量都不会增加。RevSResNet 的详细架构在表 1 中总结。RevSResNet-N 表示具有 N 层的网络。

3.4. Reversible Spiking Transformer

Basic Block:

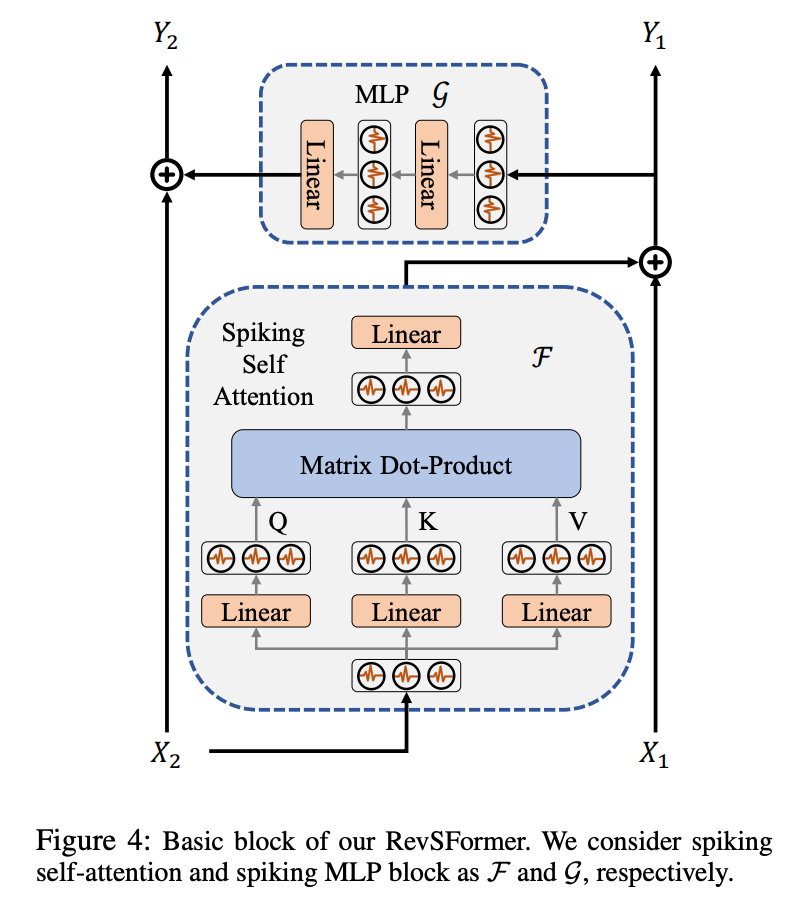
里面的具体结构和SpikingFormer是差不多的。

网络结构：

RevSFormer 的高层结构与其非可逆对应的 Spikingformer 相同。该网络包括一个脉冲分词器、L 个基本块和一个分类头。脉冲分词器计算图像的补丁嵌入，并通过多个卷积和最大池化层将嵌入投影到固定大小。分类头由一个脉冲神经元和一个全连接层组成。值得一提的是，RevSFormer 的所有下采样操作都放在脉冲分词器中。由于所有基本块之间没有其他下采样或不可逆操作，RevSFormer 只有一个由 L 个基本块组成的可逆序列。随着 L 的增加，存储中间变量所需的内存预计保持不变。RevSFormer 的详细配置与 Spikingformer 相同。RevSFormer-L-D 表示该网络有 L 个块，嵌入维度为 D。

4. Experiments

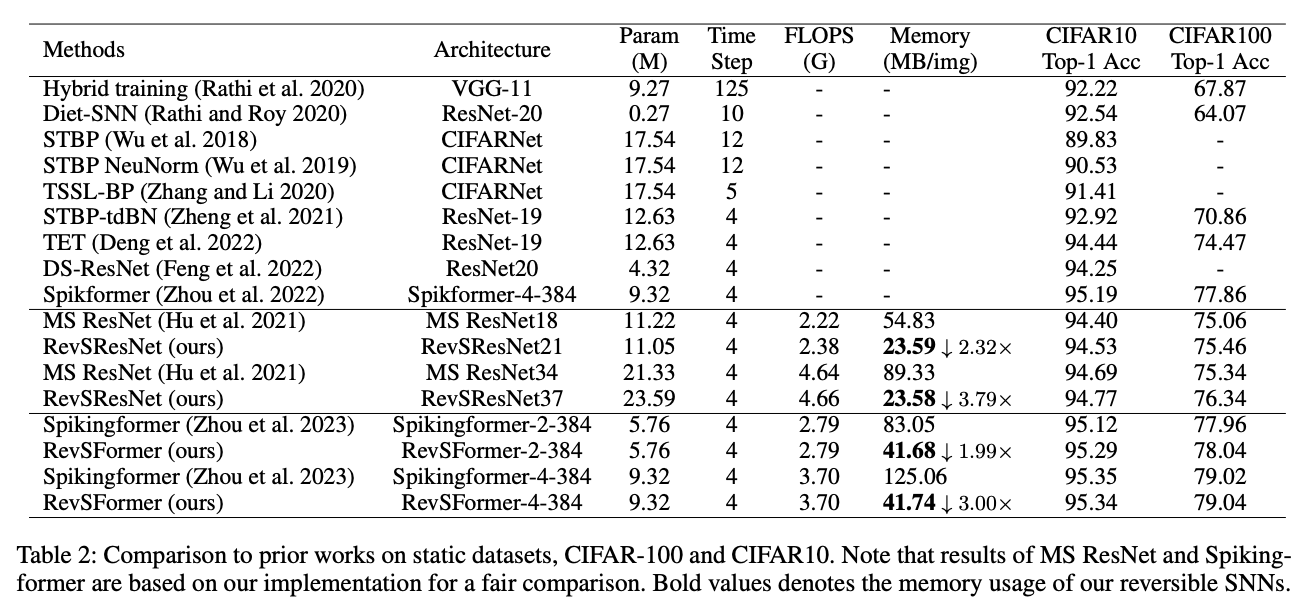
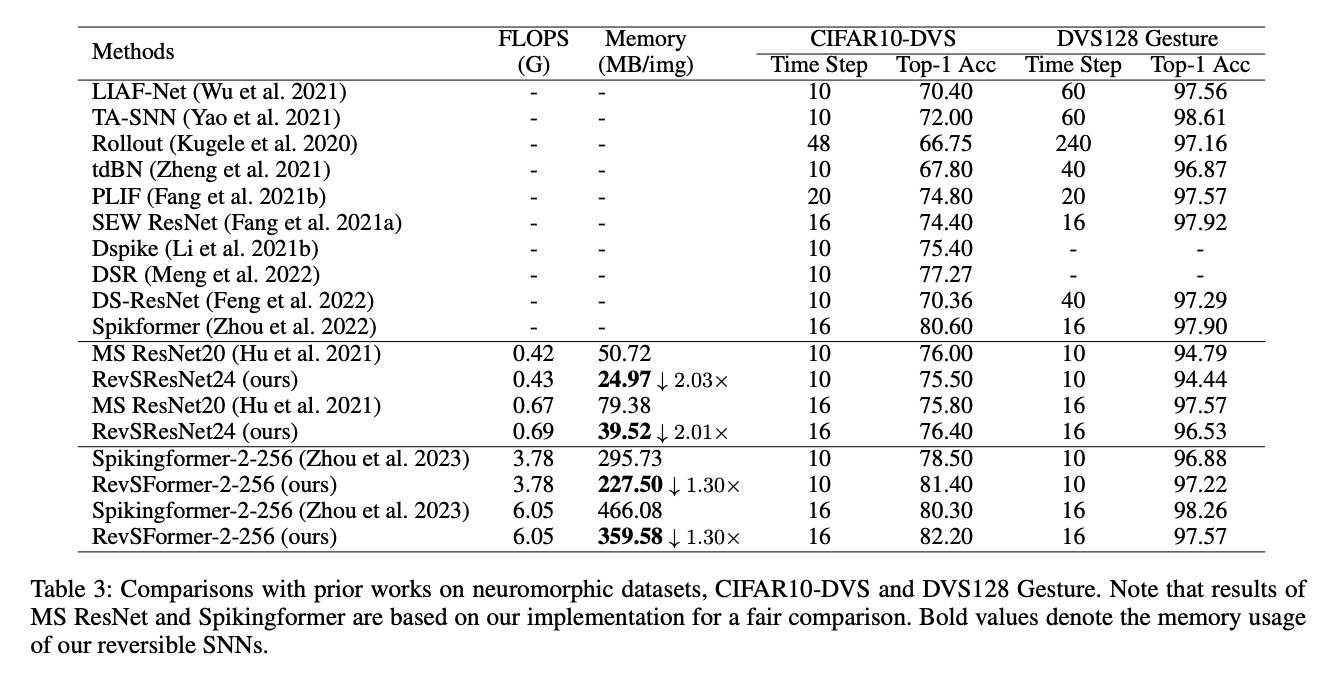
4.1. Ablation Study

4.1.1. Memory usage vs. depth

理论上，对于一个可逆序列，中间变量所需的内存使用不会随着可逆块数量的增加而增加，因为我们只需要保存整个序列的输出。因此，对于具有 4 个可逆序列的 RevSResNet 和具有 1 个序列的 RevSFormer，每张图像的内存使用不应随深度增加而增加。图 1 绘制了我们的可逆 SNNs 及其对应模型的内存使用情况。对于 ResNet 类结构，随着模型变得更深，相对内存节省幅度增加到 8.1 倍。对于 Transformer 网络，我们的 RevSFormer-16-384 每张图像节省了 9.1 倍的 GPU 内存。预计随着深度的增加，这种内存节省幅度将进一步增加。

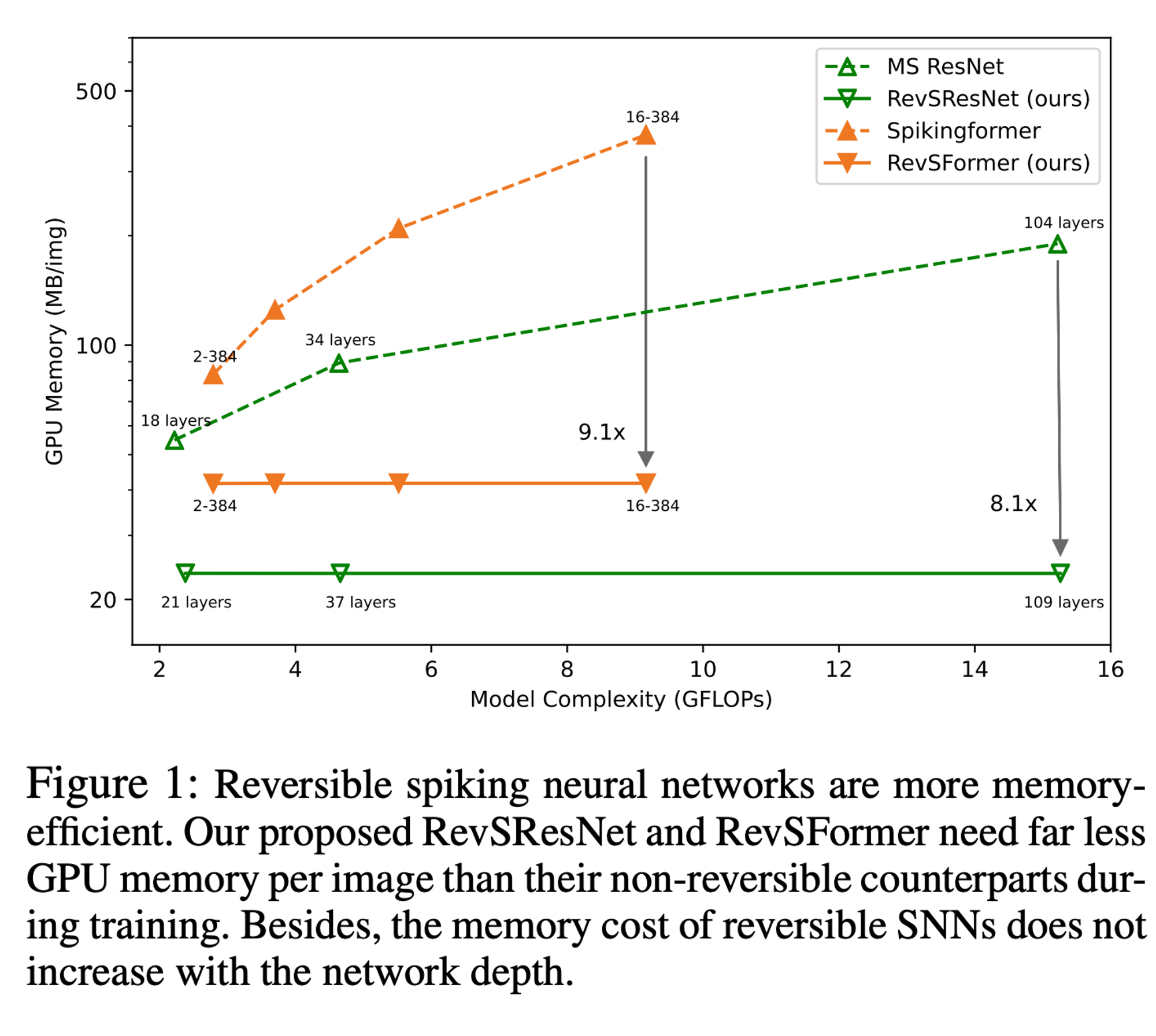
再放一次figure1，用来当teasing figure就放最前面就过看文章的时候找不到了

4.1.2. Memory usage vs. time step

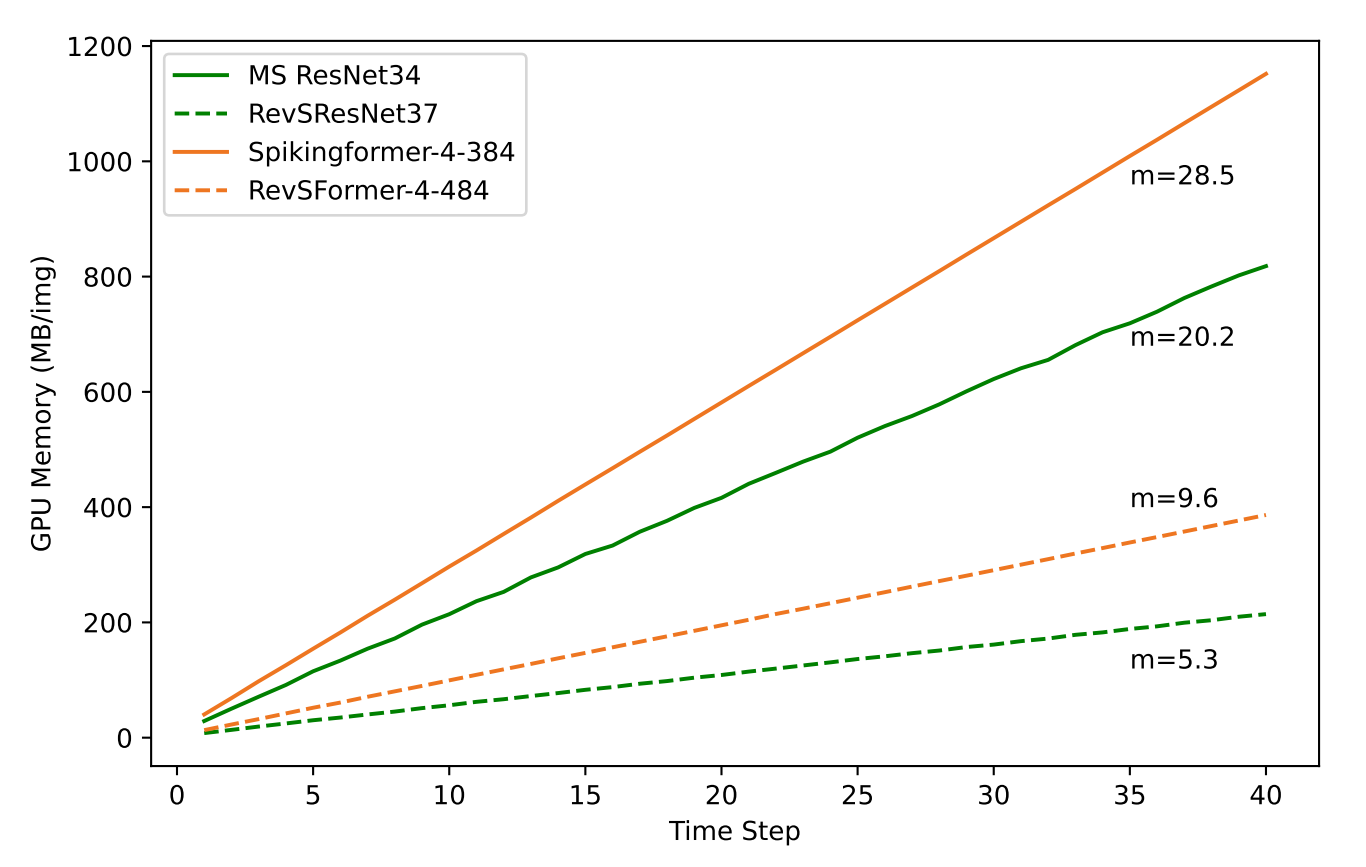
在timestep上还是要展开的，但是增长速度变慢了

4.1.3. Computational overhead during training

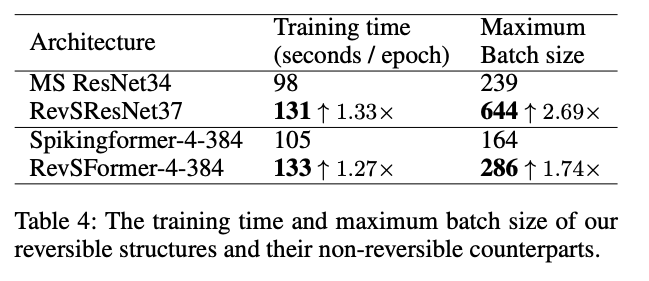
带来了额外的计算开销，但是可以开超大batch size

5. Conclusion

在本文中，我们提出了可逆脉冲神经网络，以减少 SNNs 训练过程中中间激活和膜电位的内存消耗。我们首先沿时间维度扩展了可逆架构，并提出了可逆脉冲块，可以通过反向过程重建前向传播的计算图。在此基础上，我们提出了 RevSResNet 和 RevSFormer 模型，这些模型是最先进 SNNs 的可逆版本。通过在静态和神经形态数据集上的实验，我们证明了我们的可逆 SNNs 的每张图像的内存消耗不会随着网络深度增加。此外，RevSResNet 和 RevSFormer 达到了相当的准确率，并且比其复杂度和参数大致相同的对应模型消耗了更少的 GPU 内存。

不掉性能，显存占用降低。NICE这条Flow的内容生成的路线，正向做是识别，逆向做是生成，可不可以用来做SNN+生成？

Memory-Efficient Reversible Spiking Neural Networks