摘要： 脉冲 Transformer将 SNN 与 Transformer 架构结合，因其低能耗与高性能的潜力而备受关注。然而，SNN 与人工神经网络（ANN）之间仍存在显著性能差距。为缩小这一差距，我们提出了 QKFormer——一种可直接训练的脉冲 Transformer，具有以下特点：i) 线性复杂度与高能效：创新的脉冲形式 Q-K 注意力模块利用二值向量高效建模 token 或通道注意力，支持构建更大规模模型；ii) 多尺度脉冲表示：通过在不同块中使用不同数量 token 的层次结构实现；iii) 带变形捷径的脉冲补丁嵌入（Spiking Patch Embedding with Deformed Shortcut，SPEDS）：增强脉冲信息的传递与整合，进而提升整体性能。实验结果表明，QKFormer 在多个主流数据集上均显著超越当前最先进的 SNN 模型。值得一提的是，在与 Spikformer 参数规模近似（66.34 M，74.81%）的情况下，QKFormer （64.96 M）在 ImageNet-1k 上取得了突破性的 85.65% Top-1 准确率，比 Spikformer 高出 10.84 个百分点。

1. Introduction

SNN Transformer的工作现在遇到两个挑战：

Spiking Self-Attention的计算复杂度保持 $n^2$
SNN本身还需要在一个 $T$ 的维度上进行计算

两者一起极大程度提高了显存占用、降低了计算效率。

本文提出QKFormer，包含：

Q-K Attention，一种Linear Attention
跨Block Token数量逐级递减的层级化结构
带变形shortcut的脉冲patch embedding，SPEDS模块

其中，Q-K 注意力通过二值脉冲向量执行注意力计算，实现对 #tokens（或 #channels）的线性复杂度，显著降低能耗与存储需求；层次化架构自小尺寸 patch 起步，在更深层脉冲 Transformer 中逐步合并邻域 patch、减少 #tokens，从而获得多层级脉冲特征并提升模型表现；而 SPEDS 则增强了脉冲信息的传递与整合。得益于这些设计，QKFormer 在 SNN 领域取得了最新的 SOTA 性能，突破了以往仅使用单一分辨率脉冲特征图的 Transformer-SNN 局限。

主要讲了Spikeformer, Spikingformer, Spike-Driven Self-Attention几个工作，Direct Training SNN Transformer，主要是性能还是和同规模的ANN有差距。

3. Method

3.1. Preliminary

Vanilla Self Attention

Q_{\mathcal{F}},K_{\mathcal{F}}, V_{\mathcal{F}}=X(W_Q,W_K,W_V),\\\text{VSA}(Q_\mathcal{F},K_\mathcal{F},V_\mathcal{F})=\text{Softmax}\left(\frac{Q_\mathcal{F}K^\top_{\mathcal{F}}}{\sqrt{d}}\right)V_\mathcal{F}

其中有 $\mathcal{F}$ 下标的代表是浮点数。

Siking Self Attention

Spikeformer的做法：

I=\text{SN}_I(\text{BN}_I(XW_I)), I\in\{Q,K,V\}\\\text{SSA}^\prime(Q,K,V)=\text{SN}(\frac{QK^\top}{s}V)

$s$ 是scale因子， $\text{SN}$ 是Neuron。SSA的做法避免了浮点的乘法。

3.2. Q-K Attention

Q=\text{SN}_Q(\text{BN}(XW_Q)),\quad K=\text{SN}_K(\text{BN}(XW_K))

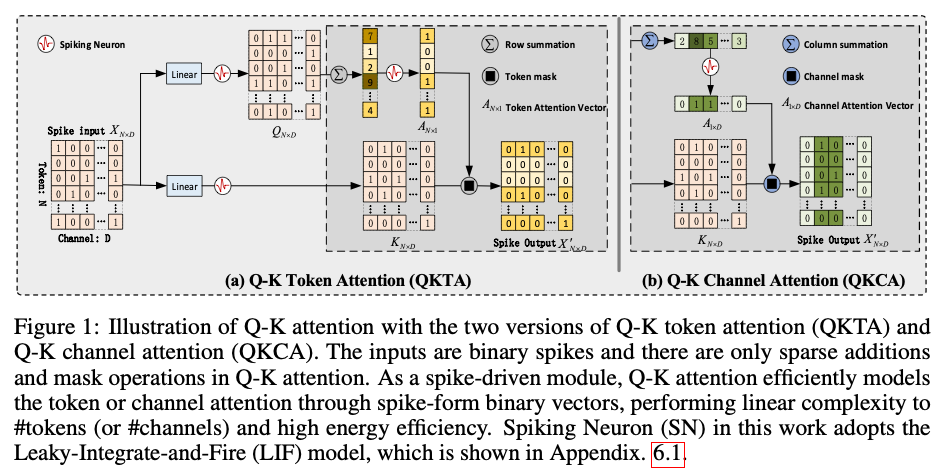
根据计算维度不同，还有Q-K Token Attention和Q-K Channel Attention两种：

Q-K Token Attention

A_t=\text{SN}(\sum_{i=0}^DQ_{i,j}),\quad X^\prime=A_t\otimes K

$\otimes$ 是逐元素乘，整个流程就是把Q按channel求和reduce然后乘到K上。注意到这一步产生了非Spike的数据（spike求和）和Spike相乘？SNN是一定要所有运算必须是Spike2Spike的吗？

Q-K Channel Attention

A_t=\text{SN}(\sum_{i=0}^DQ_{i,j}),\quad X^\prime=A_t\otimes K\\X^{\prime\prime}=\text{SN}(\text{BN}(\text{Linear}(X^\prime)))

在另一个方向上求和然后乘，经过一个Linear+Neuron又展开成Spike的模式。

Linear Computational Complexity of Q-K Attention

Higher Energy Efficiency of Q-K Attention

能效优势. Q-K 注意力把乘法替换为稀疏加法，掩码可在神经形态芯片上以寻址或逻辑与实现，几乎不耗电：

仅含 Q、K 两个脉冲张量，无 V，突触计算更少；
线性复杂度显著降低脉冲矩阵操作数量；
省去 SSA 的缩放操作，进一步节能。

3.3. No Scaling Factors in Q-K Attention

VSA为了避免梯度消失需要乘一个scale $\sqrt d$ ，但是QK Attention的输出数值很小，可以把scale去掉。

3.4 QKFormer

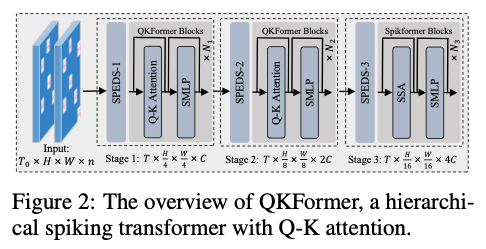
Overall Hierarchical Architecture

4*4 Patch size, 在Stage2和Stage3都要做下采样。

Mixed Spiking Attention Integration

最后一个Stage用的SSA（或者QKCA），前面用QKTA。

QKFormer Blocks

\begin{align*} X^\prime_l&=\text{QKTA}(X_{l-1})+X_{l-1}, X_l^\prime\in R^{T\times N\times D}\\ X_l&=\text{SMLP}(X_l^\prime)+X_l^\prime, X_l\in R^{T\times N\times D} \end{align*}

3.5. Spiking Patch Embedding with Deformed Shortcut

以往脉冲 Transformer 只在注意力与 MLP 块使用残差，下采样补丁嵌入处缺少恒等映射。

在Shortcut中添加一个轻量的线性变换：

Y=\mathcal{F}(X,\{W_i\})+\text{SN}(W_dX).

$W_d$ 是一个1*1卷积， $\mathcal{F}$ 是 $\text{\{Conv2D-BN-MaxPooling-SN-Conv2D-BN-SN\}}$ 或者 $\text{\{Conv2D-BN-SN-Conv2D-BN-MaxPooling-SN\}}$ 。

Patch Embedding with the pre-activation residual shorcut:

Y=\text{SN}(\mathcal{G}(X,\{W_i\})+W_dX)

$\mathcal{G}$ 类似 $\mathcal{F}$ 。文章中都用上面那个。

4. Experiments

4.1. REsults on ImageNet-1k Classification

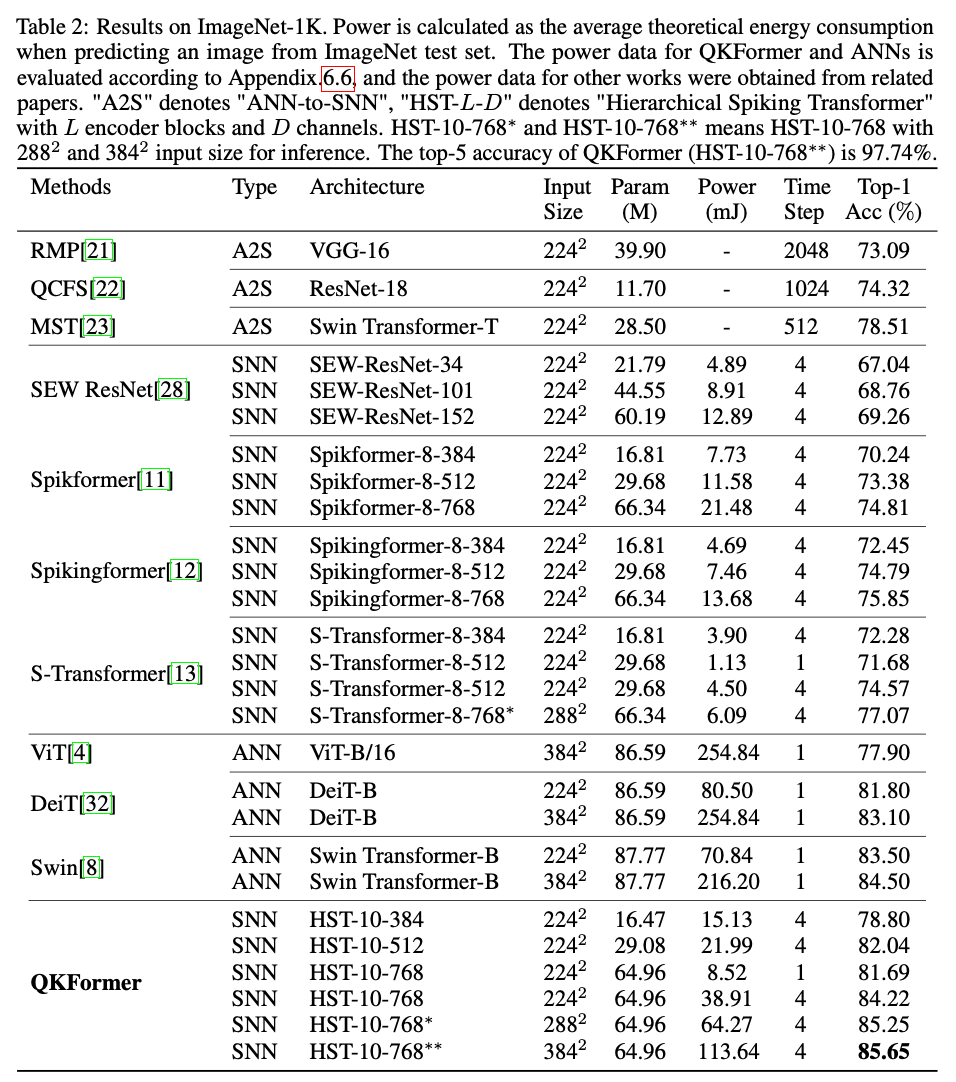
QKFormer 是首个在直接训练、4 个时间步设置下 ImageNet-1k Top-1 准确率突破 85 % 的 SNN。

4.2. Results on CIFAR and Neuromorphic Datasets

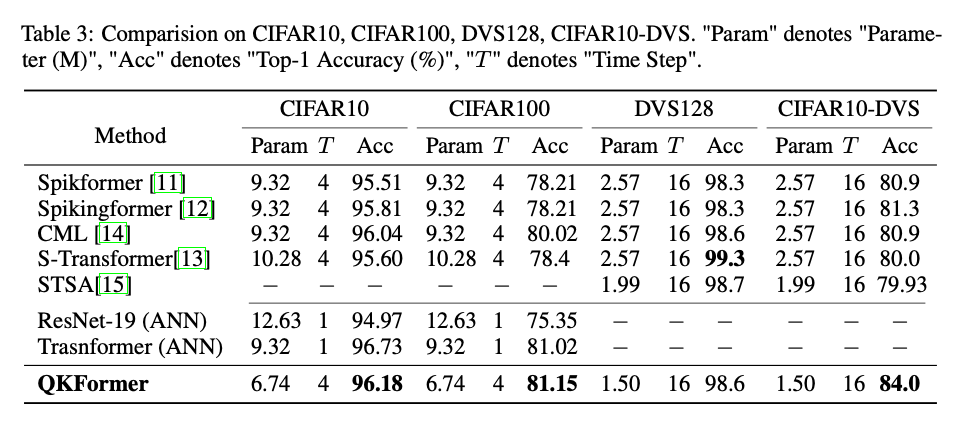
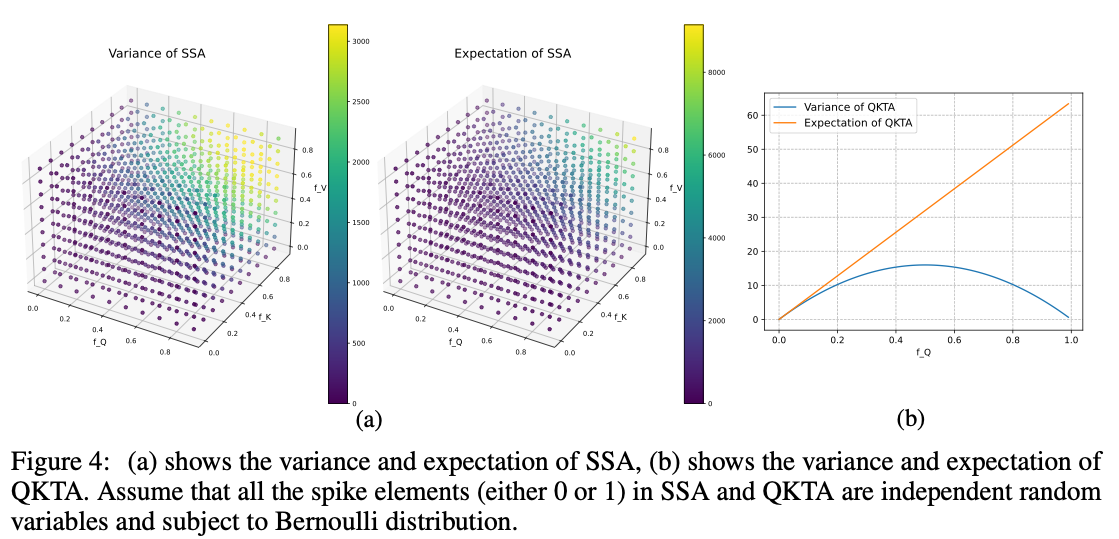
理论方差更小，所以不需要scale factor。

4.3. Analyses on Q-K Attention

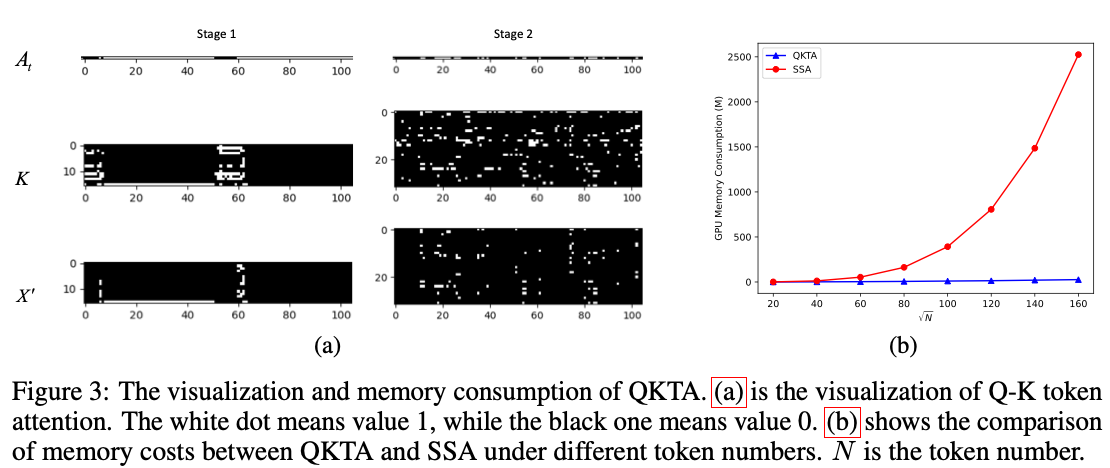
Attention Visualization

Fig3(a)，主要是看到Spike很稀疏。

Memory Consumption

显存占用更少。

Spiking Firing Rates in QKFormer Blocks

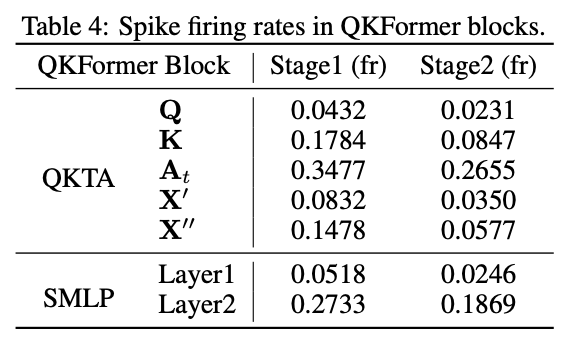
In fact, the summation operation in the Q-K attention causes Q to become significantly sparser compared to K when the network converges. Specifically, Q in stage 1 has a firing rate of 0.0432, while K has 0.1784. After the accumulation operation along $D/h$ of the multi-head QKTA version, the LIF neuron ( $A_t$ ) exhibits a typical average firing rate of 0.3477.

4.4. Ablation Study

SPEDS Module

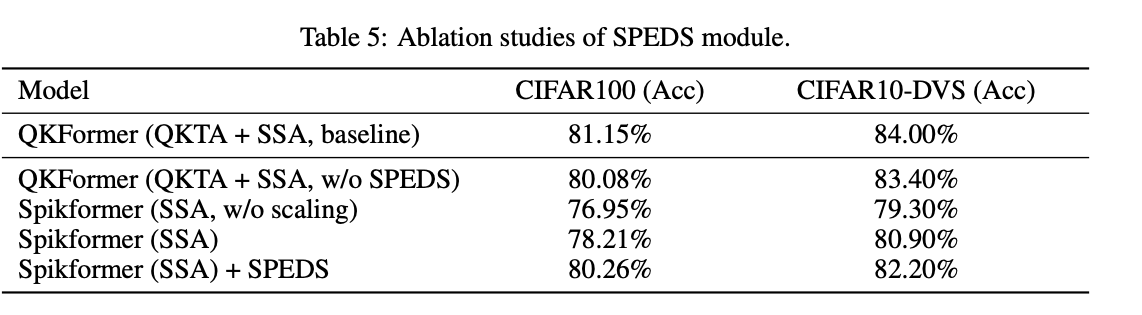
Mixed Spiking Attention Integration with Q-K Attention

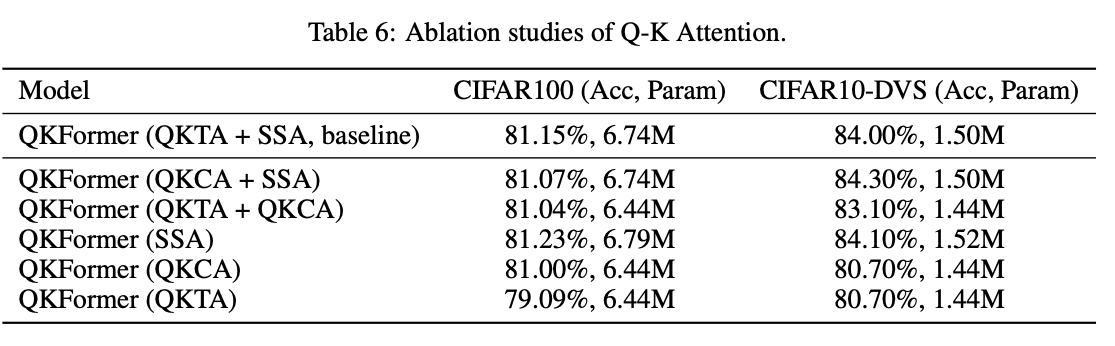
注意到混合方案效果更好而比SSA参数量更小。

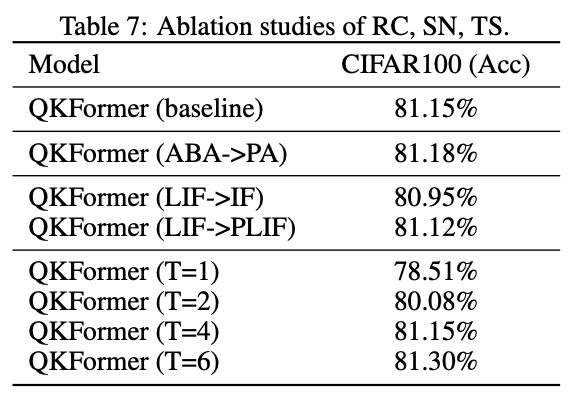
Residual Connection (RC) & Spiking Neuron (SN) & Time Step (TS)

5. Conclusion

本文针对 SNN 特性设计了新的脉冲形式 Q-K 注意力，可通过二值向量在 Token 或通道维度上建模重要性，其复杂度随 Token（或通道）数呈线性，仅含 Query (Q) 与 Key (K) 两个脉冲分量。我们提出的 Spiking Patch Embedding with Deformed Shortcut (SPEDS) 强化了脉冲信息传递与融合，显著提升脉冲 Transformer 性能。在此基础上构建的层次化脉冲 Transformer —— QKFormer，以直接训练方式在静态及神经形态数据集上均取得最新最优 (SOTA) 成绩：首次在 ImageNet-1k 上以 4 个时间步取得超过 85 % 的 top-1 准确率。期望本研究能为 SNN 的应用带来新的信心。

Limitation

目前模型仅验证于图像 / DVS 分类任务。未来我们将扩展至分割、检测及语言等更多任务，以检验通用性；同时基于 Q-K 注意力与其它高效模块，探索更少时间步下的高效高性能网络架构，以进一步降低训练消耗。

需要重新思考，什么是SNN？异步的才能是SNN？只有1/2 B Spike计算的才是SNN？

QKFormer: Hierarchical Spiking Transformer using Q-K Attention