摘要： 递归脉冲神经网络（RSNN）是一种计算高效、受大脑启发的学习模型。打造拥有更少神经元与突触的稀疏 RSNN，可显著降低其计算复杂度。传统做法通常先为某项任务训练一个稠密且复杂的 SNN，然后在保持任务性能的前提下，按“神经元活动度”剪枝（基于活动度的剪枝）以获得稀疏模型。与此不同，本文提出一种与任务无关的方法：直接从随机初始化的大模型中剪枝来设计稀疏 RSNN。我们提出新颖的 Lyapunov Noise Pruning（LNP） 算法，它结合图稀疏化技术与李雅普诺夫指数，从随机初始化的 RSNN 中构建稳定的稀疏 RSNN。我们证明 LNP 可以利用神经元时间尺度多样性，设计出稀疏的异质 RSNN（HRSNN）；同一个稀疏 HRSNN 还能被训练用于图像分类、时间序列预测等多种任务。实验结果表明，即便不依赖任务信息，LNP 仍能比传统“训练-剪枝”流程取得更高的计算效率（更少神经元与突触）与预测性能。

1. Intro

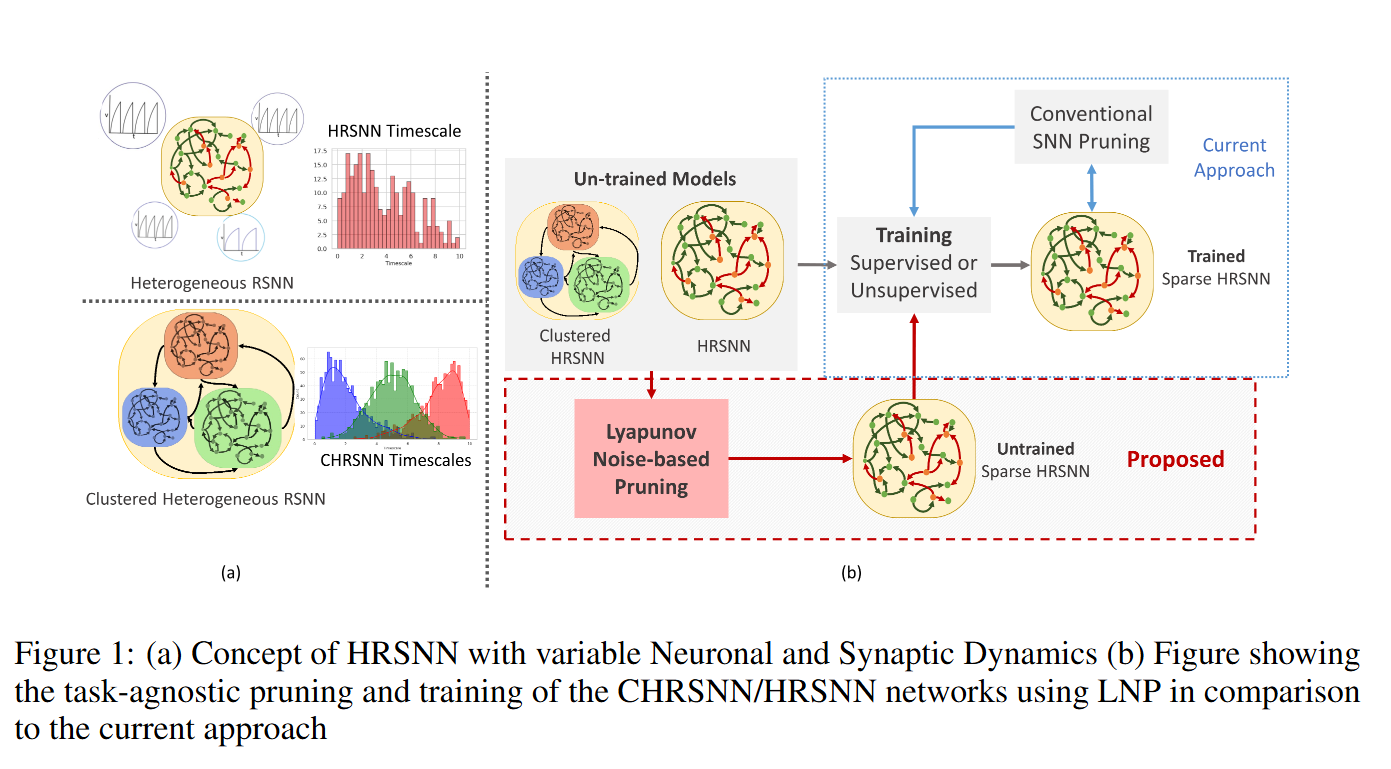
在神经元参数中引入异质性 可优化网络表现
异质性虽能提升性能，却随神经元数目呈指数级放大模型复杂度，使得超参数优化尤为困难。标准的稀疏随机初始化还会导致网络极不稳定，其李雅普诺夫谱可见一斑
传统流程是：先训练稠密网络，再剪枝神经元/突触以降低计算量并尽量减小性能损失

2. Preliminaries and Definitions

HRSNN：每个神经元的时间常数 $τ$ 由伽马分布采样，引入动力学异质性。
聚类异质RSNN：CHRSNN 的递归层由多个异质 RSNN 簇组成，每簇拥有独特的时间常数分布，然后随机连接形成“小世界”网络结构。

Lyapunov Noise Pruning Method:

3. Methods

3.1. Lyapunov Noise Pruning Method

本研究提出了一种在无监督 模型中结合谱图剪枝与 Lyapunov 指数的剪枝算法。我们先计算 Lyapunov 矩阵 ，并通过优化其比值和速率以处理极端数据并覆盖全部观测值。剪枝后，删除 介数中心性 （betweenness centrality）最低的节点以提升网络效率；随后在去局域化阶段 （delocalization phase）添加若干新边，以保持网络稳定性与完整性。该方法在结构完整性与计算效率之间实现了平衡，为网络优化提供了新途径。

Step I: Noise-Pruning of Synapses:

将原RSNN记作一个图 $G (V, E)$ ，对于连接节点 $z$ 的每条边 $e_{ij}$ ，记 $N (z)$ 为节点 $z = {i . j}$ 的邻居合集，Lyapunov指数记作 $Λ (N (z))$ 。Lyapunov矩阵 $L$ 中 $L_{ij}$ 定义为 $z = {i, j}$ 的邻居的Lyapunov指数的调和平均数：

L_{ij} = \frac{n \cdot ∣Λ ( N ( i )) \cup Λ ( N ( j )) ∣}{\sum _{λ \in Λ (N (i)) \cup Λ (N (j))} \frac{1}{λ}}

该矩阵综合了邻居节点对每条边的影响，用以评估网络的稳定性和动力学行为。

网络的行为可以线性化为：

\overset{x}{˙} = - D x + Lx + b (t) = A x + b (t)

$x$ ： $N$ 个神经元的发放率向量； $x_{i}$ 为第  $i$  个神经元发放率
$b (t)$ ：外部输入（含偏置）
$D$ ：对角矩阵，表示神经元本身的泄漏 / 兴奋性
$A = - D + L$

目标是得到稀疏网络 $A_{sparse}$ ，在保留与原网络相似动力学的同时显著减少连接：

\overset{x}{˙} = A_{sparse} x + b (t) s . t .∣ x^{⊤} (A_{sparse} - A) x ∣ \leq ϵ ∣ x^{⊤} A x ∣, \forall x \in R^{N}

上式中，所有的节点受独立噪声驱动，可以: $b (t) = b + σ ξ (t)$ ， $ξ (t)$ 是独立同分布的高斯噪声， $σ$ 是标准差，设 $Σ$ 是Spiking Rate的协方差矩阵，根据权重定义神经元 $i, j$ 之间权重的保留概率为：

p_{ij} = {ρ l_{ij} (Σ_{ii} + Σ_{jj} - 2Σ ij) w_{ij} > 0 ρ l_{ij} (Σ_{ii} + Σ_{jj} + 2Σ ij) w_{ij} < 0

其中 $l_{ij}$ 为对应的Lyapnov指数， $ρ$ 控制稀疏度。以 $p_{ij}$ 独立保留每条边，得到：

A_{sparse_{ij}} = {\frac{A _{ij}}{p _{ij}} 0

$A_{sparse_{ii}}$ 表示了漏电权重或者兴奋性，可以：

保留原值，或者
引入一个微扰 $Δ_{i}$ ，即：

Δ_{i} = j \neq = i \sum ∣ A_{sparse_{ij}} - j \neq = i \sum ∣ A_{ij} ∣, A_{sparse_{i} i} = A_{ii} - Δ_{i}

Step II: Node Pruning based on Betweenness Centrality

使用 $C_{b}$ ”betweenness centrality“衡量一个node对网络信息流的控制能力。计算每个node的 $C_{b}$ 然后根据threshold剪枝。

Step III: Delocalizing Eigenvoctors

剪枝可能导致特征向量局域化并损害长时预测。在做完上面的pruning得到 $G^{'} = (V, E^{'})$ 之后，添加额外的边集 $E^{''}$ ，从而最大化整个图的度分布方差（异质性），并保证 $∣ E^{'} \cup E^{''} ∣ \leq L$ ：

H = \frac{1}{∣ V ∣} v \in V \sum (d (v) - \overset{ˉ}{d})^{2}, E^{''} max H, s . t .∣ E^{''} ∣ = m, E^{''} \cap E^{'} = \emptyset, E^{''} \subseteq v_{i} \in V ⋃ N (v_{i}) \times v_{i}

此优化确保在既定稀疏度下维持结构完整性与特征向量的非局域化，从而提升长期预测性能。

Step IV: Neuronal Timescale Optimization

剪枝后的脉冲式 SNN（RSNN）动力学更加复杂且易不稳定。参考 Vogt 等 (2020)，我们将 Lyapunov 谱 用作稳定性指标，在 ** 贝叶斯优化** 框架下调节神经时间常数，既保持网络功能又抑制由剪枝带来的不稳定风险。

4. Experiments and Results

4.1. Experimental Setup

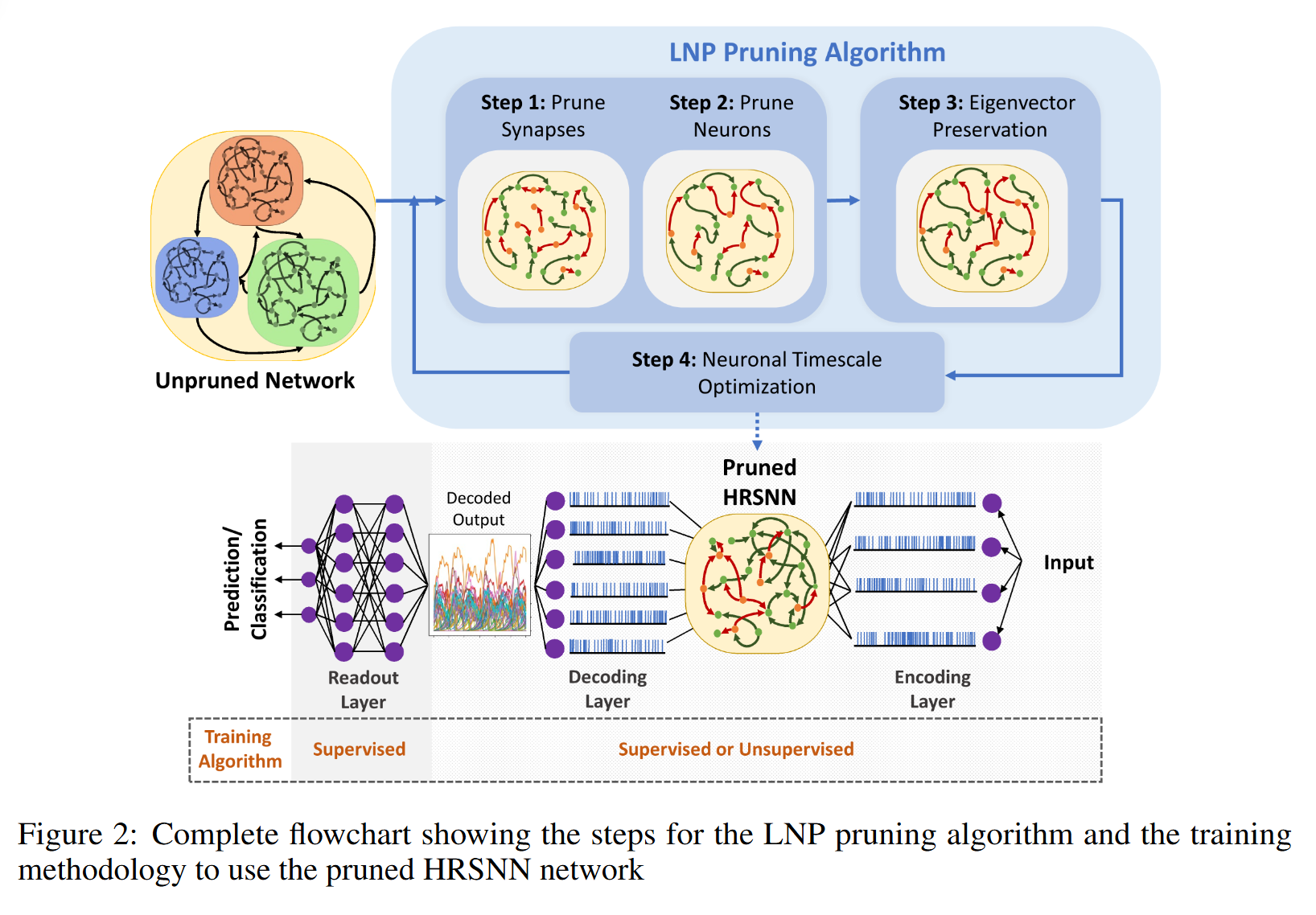
通过剪枝算法得到稀疏网络。每执行一次剪枝，就会产生一个新的稀疏网络；我们共进行 100 次剪枝迭代 。在每次迭代后，我们统计得到的 “Sparse HRSNN” 的神经元与突触分布，用来跟踪模型复杂度随剪枝的下降情况。

预测任务 ：在数据集的 500 个时间步 上训练网络，然后预测接下来的 100 个时间步 。
分类任务 ：每张输入图像在 100 ms 的仿真时间内以泊松（Poisson）脉冲列输入，脉冲发放率与像素强度成正比；随后再输入 ** 100 ms** 的空信号以便神经元活动衰减。

Evolution of Complexity of Sparse Models during Pruning

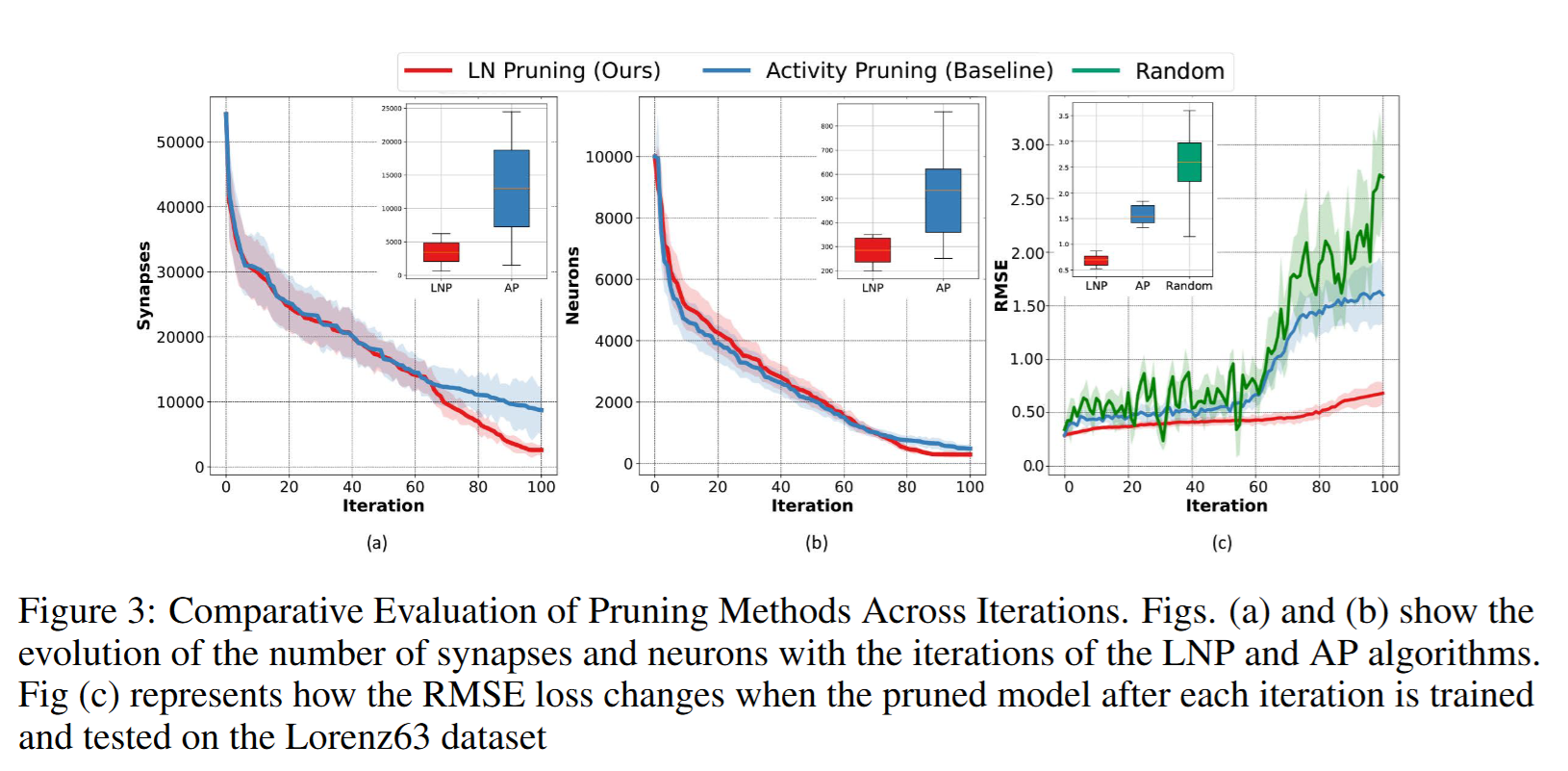
随机初始化网络方差更大、波动更多，说明在缺乏微调时模型不稳定；并且随着模型规模缩小，性能持续下降，提示 小模型更依赖合理的拓扑 。对比之下，AP 模型最终的突触与神经元分布方差都高于 LNP，进一步说明 LNP 的稳定性。

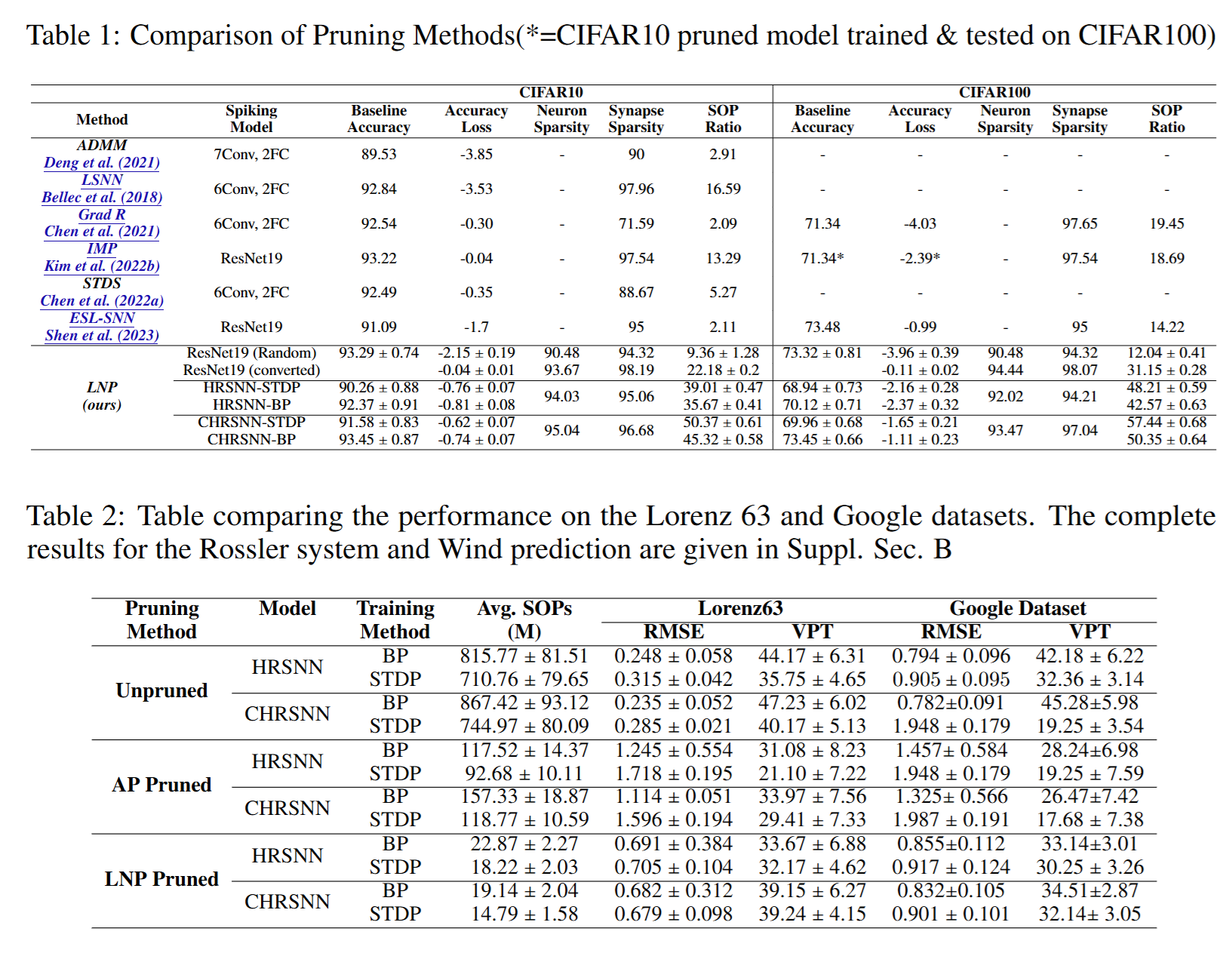
Energy计算方法： $E = C_{E} \times Total SOPs$

Ablation studies

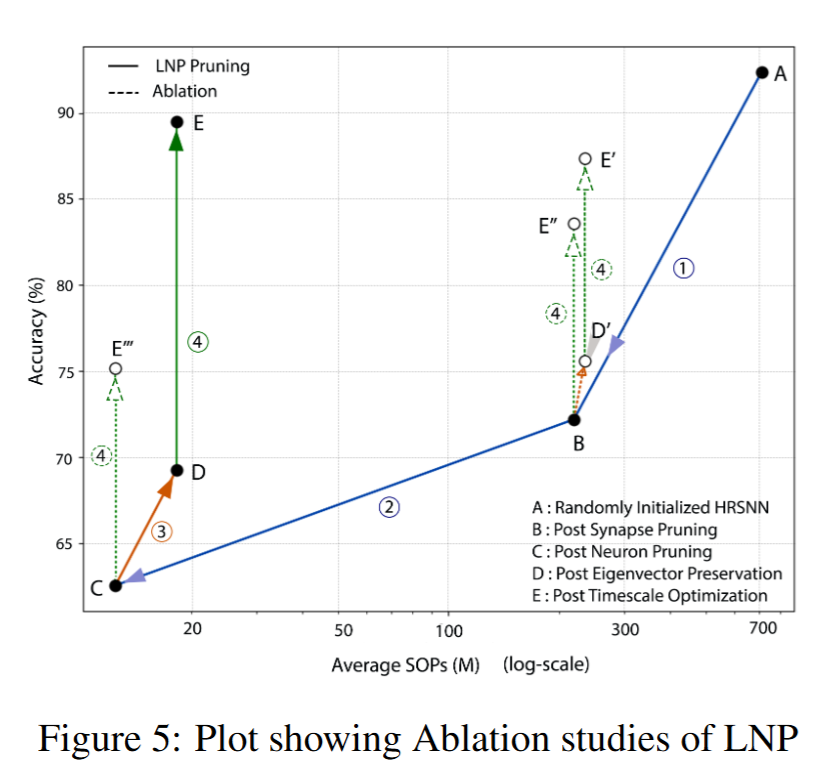
5. Conclusion

本研究提出了 Lyapunov 噪声剪枝（LNP） —— 一种全新的、** 与任务无关的稀疏递归脉冲神经网络（RSNN）设计方法，重点在于在 ** 计算效率 与 ** 最优性能** 之间取得平衡。与现有方法不同，LNP 以随机、密集初始化的 RSNN 为起点，利用 ** Lyapunov 谱** 与 ** 谱图稀疏化** 技术在保持网络稳定性的同时进行剪枝。实验结果表明，LNP ** 优于传统的基于激活剪枝**：在减少神经元与突触数量、降低计算复杂度的同时，仍在多个合成与真实数据集上保持更高的准确率与预测有效性。其任务无关的特点使模型具有 ** 普适性与鲁棒性**，无需大量针对特定任务的调参，即可保留关键网络参数并优化模型结构——这一点在计算资源受限的环境中尤为重要。此外，LNP 训练得到的模型位于 ** 更平坦的损失极小值**，对应更稳定、鲁棒的解，从而提升了学习到的动态行为的稳定性。总之，LNP 在神经网络设计方面实现了重要突破，能够提供 ** 更高效、稳定且多用途** 的模型，适用于多样化应用，并为神经网络领域的未来创新奠定了基础。

Appendix

A.1. Computation of Lyapunov Expenents

我们采用经典算法，并遵循 [48, 55] 中的实现方式来计算 Lyapunov 指数（LE）。针对某一具体任务，每个批次的输入序列都从同一分布、固定长度的验证集序列中随机抽取。对批次中的每条输入序列，都先将矩阵 Q 初始化为单位矩阵，用来表示一组正交的邻近初始状态；隐藏状态 $h_{t}$ 初始化为零。

在step $t$ ，计算 $J_{t}$ 并且应用到 $Q$ ，雅可比矩阵 $J_{t}$ 定义为：

[J_{t}]_{ij} = \frac{\partial h _{t}^{j}}{\partial h _{t - 1}^{i}}

除了隐藏状态 $h_{t}$ 之外还取决于输入。从而描述网络对外部刺激的动力学响应。通过对 $J_{t} Q_{t}$ 做QR分解得到新的 $Q_{t + 1}$ 和上三角矩阵 $R_{t + 1}$ ，从而提取新的扩张因子：若 $r_{t}^{k}$ 是第 $k$ 个向量在 $t$ 时刻的扩张因子（ $R_{t}$ 的第 $k$ 个对角元），则对于长度为 $T$ 的输入序列，有：

λ_{k} = \frac{1}{T} t = 1 \sum T

一个Batch中每个都计算Lyapunov谱然后取平均，对较短的做插值和较大的保留一致。

离散视角下：

h_{i} (t + Δ t) = (1 - Δ t) h_{i} (t) + Δ t j \sum J_{ij} φ (h_{j} (t))

Jacobian:

D_{ij} (t_{s}) = \frac{\partial f _{i}}{\partial h _{j}} ∣_{t = t_{s}} = (1 - Δ t) δ_{ij} + Δ t \cdot J_{ij} ϕ^{'} (h_{j} (t_{s}))

Lyapunov 指数 (LE) 描述相邻轨迹在相位空间中的平均指数级分离速率。
正值 → 对初始条件敏感 → 潜在的混沌；** 负值** → 收敛；** 零** → 边界轨迹。
在 RNN / RSNN 中，LE 揭示了信息记忆时长、梯度爆炸/消失与可训练性。

QR-基算法原理

邻域正交向量集 ：单位矩阵 Q₀ 提供 n 条彼此垂直的微扰方向。
线性化演化 ：每一步用雅可比 Jₜ 逼近局部线性变化，更新扰动 ** Jₜ Qₜ**。
正交化 ：若直接累乘会数值崩溃；Gram-Schmidt（QR）在每步重新正交并分离尺度：
$J_{t} Q_{t} = Q_{t + 1} R_{t + 1}$

其中对角元 $r_{t}^{k}$ 记录第 k 向量的放大率。

时间平均 ：取 $lo g r_{t}^{k}$ 并累平均即得 $λ_{k}$ 。长序列保证渐近稳定。

A.2. Linearization Around Critical Points

描述的是Methods部分中的重复内容？

为什么先线性化再剪枝？

可判定稳定域 ：若 A\mathbf AA 在单位圆／左半平面内 → 稳定。剪任何边前先看会否让谱穿出稳定域。
可计算重要度 ： $L$ 把 Lyapunov 指数映射到边；协方差 $Σ$ 把输入驱动映射到节点关系。二者合成 $p_{ij}$ ，即“删了这条边，扰动能量会放大多少”。
剪后易校正 ：稀疏化引入误差 $A_{sparse} - A$ 。因误差已在二次型上受控，后续再通过 步骤 III 补边 与 ** 步骤 IV 时间尺度调优** 就能恢复性能。

Sparse Spiking Neural Network: Exploiting Heterogeneity in Timescales for Pruning Recurrent SNN