摘要： 近年来，关于深度神经网络剪枝和压缩的研究呈现出爆发式增长。早期的方法是对权重逐个进行剪枝。然而，在现代硬件（如GPU）上，很难利用这种剪枝带来的非结构化稀疏性。因此，逐渐兴起了通过施加稀疏结构的剪枝策略。然而，这些结构化剪枝方法通常比非结构化剪枝带来更大的精度损失。本文提出了一种名为SparseRT的代码生成器，能够利用非结构化稀疏性加速GPU上深度学习推理中的稀疏线性代数操作。在1x1卷积和全连接层的场景中，我们展示了在90%的稀疏度下相对于等效的密集计算实现了3.4倍的加速，而在95%的稀疏度下达到了5.4倍的加速，这些数据是在数百个深度学习测试用例上验证的。对于3x3卷积层的稀疏性，我们在ResNet-50中的用例中展示了超过5倍的加速效果。

1. Intro

GPU的设计不适合非结构化的稀疏，之前的稀疏计算基本是在结构化稀疏的前提下做的。现在做模型剪枝这样的工作很多，但是加速很少。现在有的稀疏矩阵乘（SpMM）主要是针对科学计算的领域做的，需要非常高的度，并且稀疏矩阵的维度需要远大于稠密矩阵，在神经网络方向不太合适。

在这项工作中，我们提出了SparseRT，一种用于SpMM和稀疏卷积内核的代码生成器，专为深度学习推理场景设计，基于检查-执行（inspector-executor）优化框架，并采用PTX代码生成作为后端。在SparseRT中，我们不局限于某种稀疏矩阵格式的特点，而是从密集矩阵乘法出发，在检查-执行框架中简单地移除不必要的计算。在最新的GPU上进行评估时，我们展示了在90%稀疏率下SpMM的几何平均加速为3.4倍，而在95%稀疏率下达到了5.4倍的加速，这些结果基于计算机视觉和自然语言处理剪枝神经网络的数百个测试矩阵。此外，通过将稀疏卷积降低为SpMM问题，我们在ResNet-50中的3x3稀疏卷积上实现了高达4倍的加速

SpMM Performance：科学计算中SpMM的对象更像是一些小向量集合，稠密矩阵的维度比较“skewed”，但是在神经网络中不是这样。在DeepBench中SpMM在Titan XP上用cuSPARSE比直接算稠密矩阵乘还要慢十倍。
Inspector-Executor Framework：可能2020年的时候“深度学习编译器”这种叫法还不太火；
Autotuning

3. Design Principles For Fast SpMM

SparseRT 采用检查-执行（inspector-executor）框架。在编译时，稀疏权重矩阵是已知的。稀疏矩阵首先被视为密集矩阵，将问题转化为矩阵乘法（GeMM）。随后，我们针对该 GeMM 问题探索不同的分块策略。对于每种分块策略，我们重新平衡并删除涉及原始稀疏矩阵中零值的计算，从而生成经过优化的 PTX 或 CUDA 执行器代码。最后，我们进行自动调优，寻找最快的执行器。

3.1. CUDA Programming Model

一个CUDA程序包含多个_thread_，每个_thread_私有一些寄存器，寄存器的效率高但需要控制总量；GPU还提供一些_constant cache_，存储在编译的时候就已知的一些常量，效率也比较高。

GPU一般会让32个 _thread _（一个 _wrap _）在每个cycle内执行相同的指令，如果 _wrap _内的指令不同的话会导致严重的 _wrap divergence penalty 。一个_thread group_可以包含一个或者多个_wrap。

多个_thread group_构成一个_thread block_，每个_thread block_独占一片_scratchpad_用于_thread_间通信。一个_kernel_包含多个_thread block_，它们之间通信的非常少。

要写一个高性能的kernel必须保证thread group之间的load balance，因为一个thread block需要等待所有的thread group全部结束才能退出。在稀疏的计算中，thread block的计算量和需要处理的非零元素大致相等，所以不同的thread block需要分到相近的非零元素。

3.2. Terminology

矩阵乘：

A\times B=C

维度是 $M\times K\times N$ ，称 $M, N$ 为external axis， $K$ 为reduction axis。假设是row major的布局， $A$ 是稀疏的而 $B$ 是稠密的。

3.3. Densify and Tile

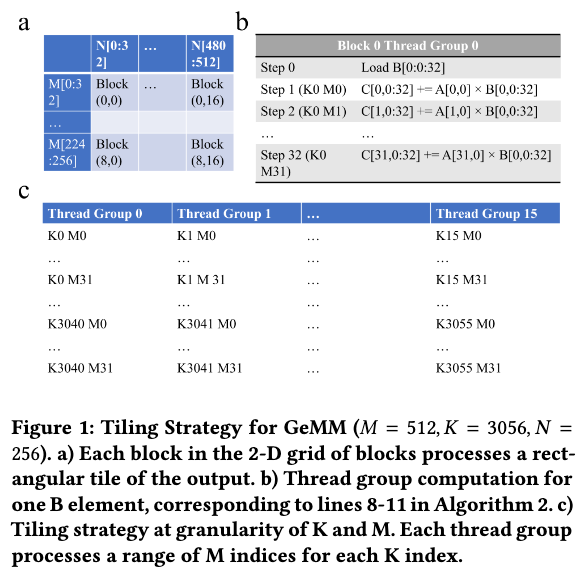
按照external axis分块，每个thread block分到一块，处理所有的对应的 $K$ 。thread block内的多个thread group再计算不同的 $K$ 分块，保存在自己的寄存器中，结束的时候通过共享内存汇总。

3.4. Load Balancing

密集的矩阵乘只要按照上面这种分块直接算就可以了，但是稀疏的矩阵乘面临的问题是，thread block虽然处理相同大小的 $A$ ，但是其中包含的非零元素不一定相同。文章提出两种负载均衡的方式如下图：

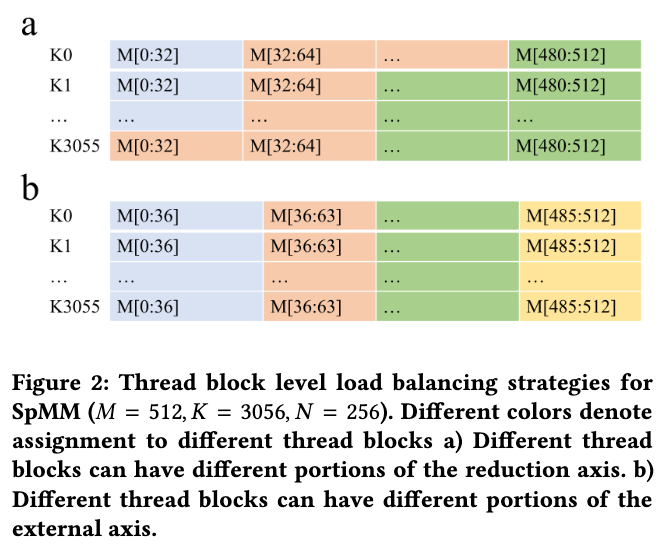
保持 $M$ 轴上的元素数量不同，给每个thread block分配不同的 $K$ 数量；
保持 $K$ 相同，但是 $M$ 不同。

方法1的粒度更细，但是分块的逻辑和写回的策略很复杂；方法2简单一些，但是在申请寄存器的时候，CUDA不允许给不同的thread block分配不同数量的寄存器，而每个thread block分到的寄存器和 $M$ 相关，所以会导致寄存器的浪费。

文章选择了方法2，因为测试表明ML任务中的稀疏模式不会导致很明显的寄存器负载不均衡。

3.5. Code Generation

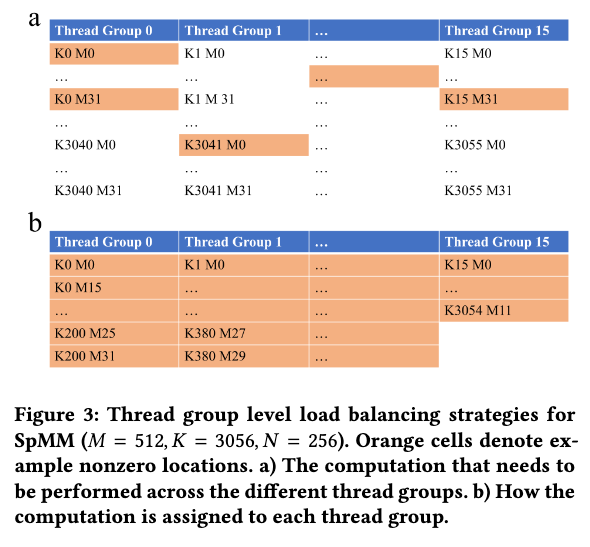
在做代码升成的时候还需要像上图这样，把稀疏的vector聚合在一起，避免在CSR数据结构中遍历寻址。并且生成代码的时候还会把上面算法3的9-11行那个循环做展开。

3.6. Supporting Convolutions

用im2col。做3*3卷积支持的时候原本需要处理比较复杂的padding等问题，可能涉及到wrap内分支预测的问题。但是所有循环都被展开了，可以直接在编译的时候解决这个问题，提高效率。

3.7. Autotuning

问题包含的参数并不多，按照：

分块大小，thread group数量；
thread block大小和kernel的内存用量符合GPU架构要求；

进行启发式搜索，一般组合数量不超过100个，实践中调优时间不到两分钟。

生成PTX代码而不是CUDA代码是为了减少NVCC编译的时间。激进的循环展开导致文件特别大行数特别多，编译时间特别长，所以直接生成PTX代码可以显著减少时间。

理论上，最佳参数不仅取决于矩阵的维度和稀疏度，还取决于稀疏模式。在稀疏神经网络推理中，相同矩阵维度和稀疏度的 SpMM 或稀疏卷积问题可能具有不同的稀疏模式，因为现代神经网络通常会重用层。例如，在第一个瓶颈组中的所有 3x3 卷积层的 SpMM 操作维度相同，但稀疏模式不同。在 Transformer 架构中， $M=512,K=512,N=256$ 的 SpMM 实例可能有多达 72 种。如果资源允许，针对每个问题实例进行调优可以实现最佳性能。然而，我们发现，在实践中，这些实例的稀疏模式相似度足够高，仅对其中一个实例进行调优就已足够。

4. Evaluation

对比对象包括cuBLAS，cuSPARSE，cuDNN。稀疏的格式、计算卷积采用的算法（FFT，Winograd，im2col）等都取对应任务中表现最好的。文章没有实现算子融合等工作所以benchmark是从ResNet50、MobileNetv1、BERT中抽取的不同的层。

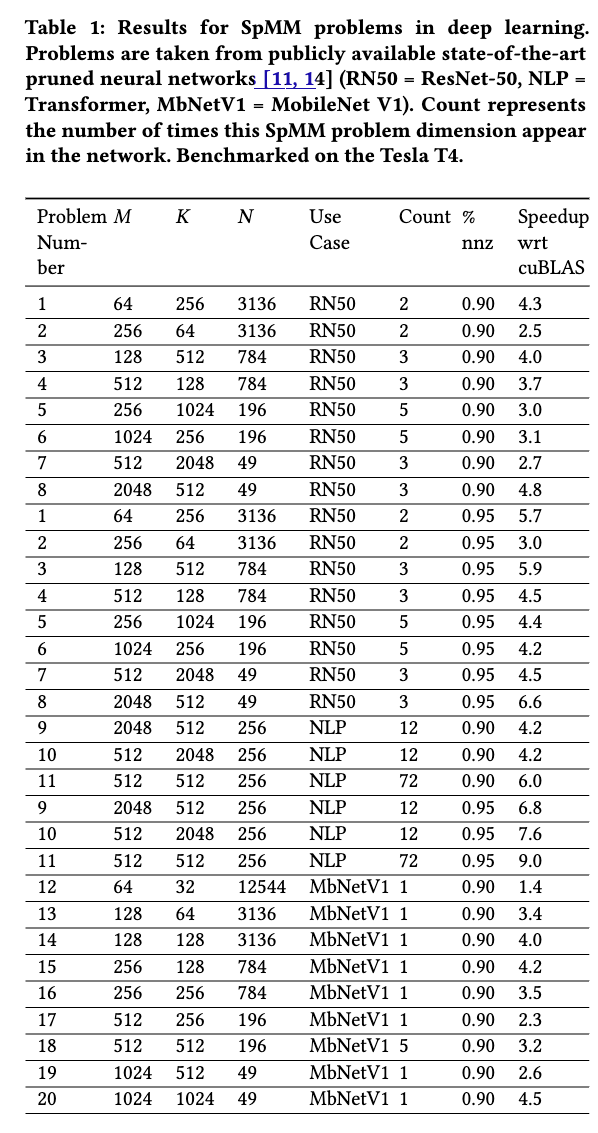
在Tesla T4和V100-SXM2做实验。

4.1. SpMM

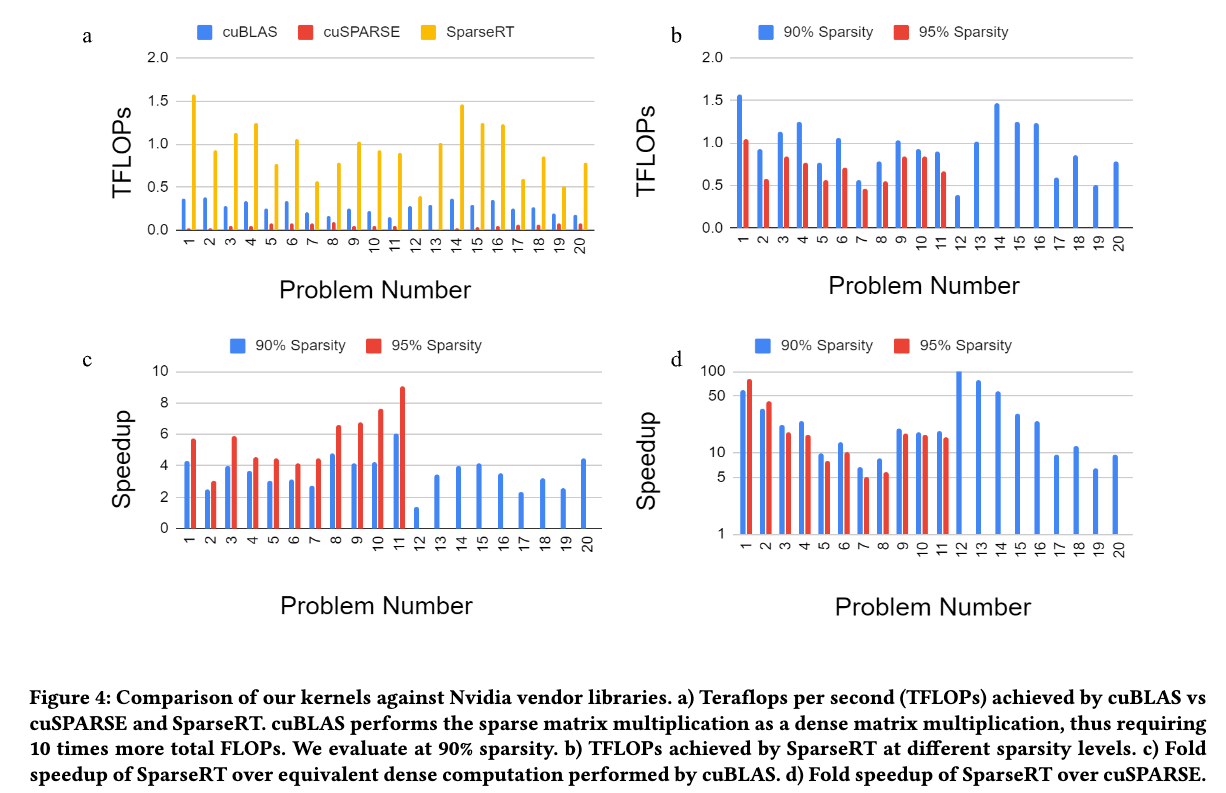
4(a)：SparseRT效率比cuBLAS和cuSPARSE都高；cuBLAS直接硬算稠密在90%稀释度下都比cuSPARSE快；注意到 $N$ 减小而 $M,K$ 增大的时候，SparseRT的性能下降（分块策略受影响）而cuSPARSE性能上升（更符合科学计算的范式）
4(b)：稀疏度上升，SparseRT的性能反而下降；
4(c)：相比于cuBLAS基本都有speedup，注意到不同 SpMM 问题的加速水平变化很大；
4(d)：相比于cuSPARSE speedup很高；可以做出结论：当前最先进的稀疏线性代数库也不适合深度学习任务

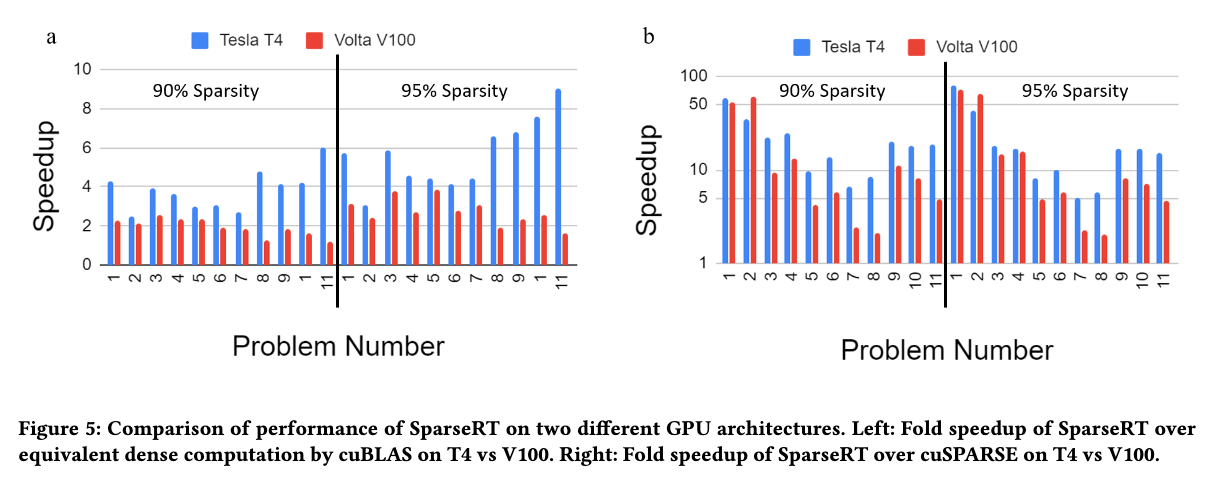
不同GPU上的测试，表现稳定，是可移植的。

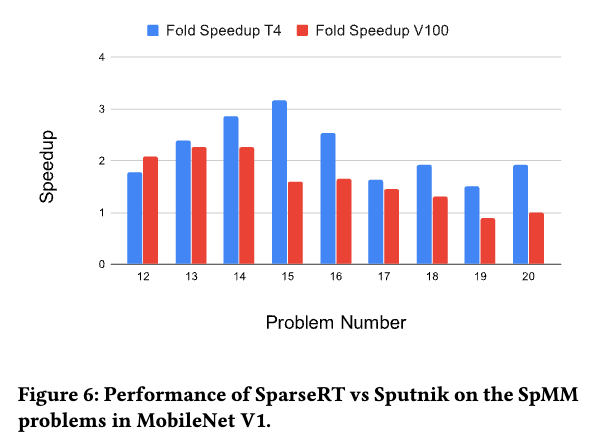
和同类工具Sputnik对比，也有一定的优势。

Sputnik 结合了多种优化技术，如 行重排序 、内存对齐 和 ** 子 warp 分块**。它在推理性能上相比于 ASpT 和 cuSPARSE 等最先进的基准实现了显著提升，并在 MobileNet V1 推理中展示了端到端的加速……在较小的稀疏矩阵问题上，SparseRT 的表现优于 Sputnik，而在较大的稀疏矩阵问题上，两者的性能相当。

4.2. Sparse Convolution

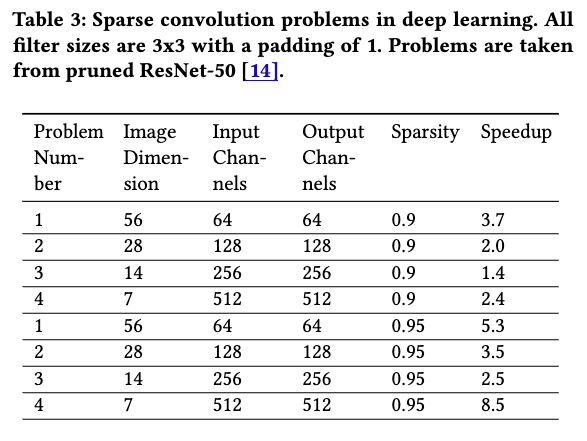
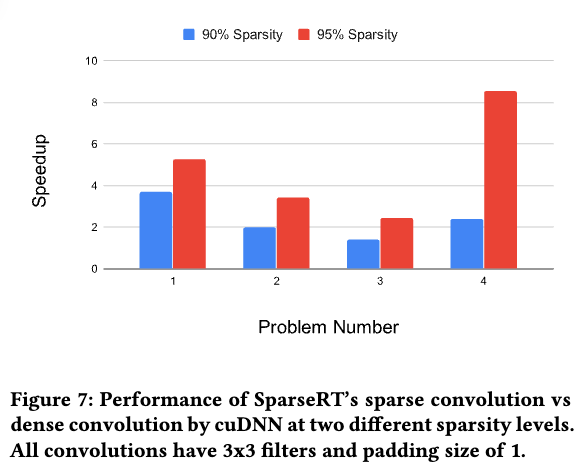
有一些benchmark中cuDNN选择的是Winograd而不是im2col，但是依然有加速比。

与 SpMM 类似，我们发现，随着稀疏权重的规模增大，获得的加速比有所下降，但 问题 4 是一个显著的例外。我们将在下一节中详细解释其原因。

4.3. Ablation Studies and Performance Analysis

从图 4 可以看出，当稀疏矩阵相对于稠密矩阵较小时（如问题 1 和 3），SparseRT 相对于 cuBLAS 和 cuSPARSE 取得了最大的加速。而在稀疏矩阵比稠密矩阵大的情况下（如问题 6 或 7），SparseRT 对 cuBLAS 的加速效果较弱。这种现象如何理解呢？

如果是稠密矩阵乘，一般是compute bound，设计网络架构的时候也会考虑到这一点，整个网络中矩阵乘法运行时间的变化并不大；而稀疏矩阵乘一般是memory bound，而SparseRT采用了很激进的循环展开策略，这样操作的时候实际上只从constant cache和shared instruction memory等片上缓存中取数据，减小了缓存的争用，带来了巨大的性能提升。

由于代码展开策略的使用，当稀疏矩阵非常大时，SparseRT 的内核往往受到 指令获取延迟 的限制，而非内存或执行依赖的限制。当 $M$ 和 $K$ 增加时，** 64KB 常量缓存**会被耗尽，此时编译时常量会被编译为指令中的立即数，这比使用常量缓存效率低。因此，我们发现 SparseRT 内核的运行时间与 $M \cdot K$ 成正比，而不是 $M \cdot N \cdot K$ 。尽管如此，在 $M \cdot K$ 非常大的情况下（如问题 6 或 7），SparseRT 仍然比 cuBLAS 更高效。与 Sputnik 的对比（如 图 6 所示）也验证了这一趋势：当稀疏矩阵较小时，SparseRT 的表现优于 Sputnik；而当稀疏矩阵较大时，Sputnik 能追赶上 SparseRT 的性能。 cuSPARSE 内核的运行时间则呈现出与 SparseRT 内核相反的趋势：当稠密矩阵相对于稀疏矩阵较大时，cuSPARSE 表现更好。这是预期的，因为 cuSPARSE 针对科学计算中的场景进行了优化，其中稀疏矩阵通常比稠密矩阵大得多。正如 图 4d 所示，在神经网络早期层中的 SpMM 问题中（其中 $M$ 和 $K$ 很小），SparseRT 相比于 cuSPARSE 的优势非常显著（超过 50 倍）。但随着 $M$ 和 $K$ 相对于 $K$ 的增加，SparseRT 的优势逐渐减弱。

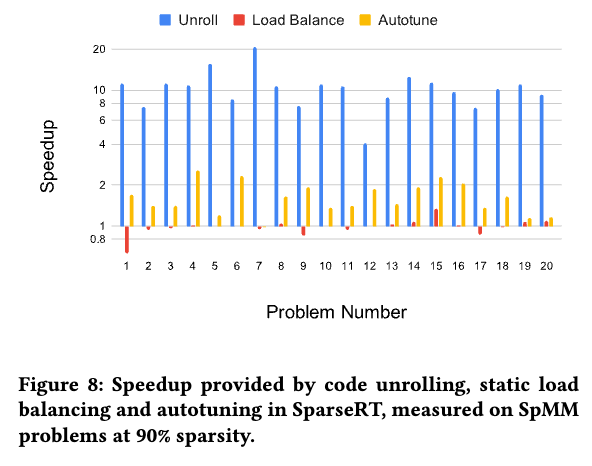
当我们不在线程块之间对稀疏矩阵进行负载均衡时，大多数情况下性能相当，甚至在某些问题中还出现了性能提升。这可能是因为常见剪枝技术得到的稀疏矩阵的稀疏模式本身比较均匀。这里使用的静态负载均衡技术根据不同线程块分配不同数量的稀疏矩阵行，这导致每个线程块使用不同数量的累加寄存器。由于 GPU 硬件无法动态分配寄存器，必须为所有线程块分配相同的最大寄存器数量，这可能会导致资源浪费。为了研究自动调优的效果，我们对每个问题固定一个参数组合。这导致大多数问题的运行时间约减慢了 2 倍 ，这证明了自动调优对我们方法的益处。由于我们优化的是推理，因此自动调优的成本可以通过所有后续推理请求进行有效摊销。

我们发现，SparseRT 在处理小矩阵时相较于 Sputnik 有 ** 2-3 倍** 的性能提升，而在处理较大矩阵时性能与 Sputnik 相当。这一趋势是预期的，因为 SparseRT 在较大的稀疏矩阵上性能相对较差。SparseRT 在 Tesla T4 上的优势比在 V100 上更明显，这可能是因为 ** Sputnik** 针对 V100 架构进行了优化 [15]。虽然 SparseRT 和 Sputnik 在某些优化策略上有相似之处，如将稠密矩阵列并行分配给线程块，但两者的方法本质上不同。

Sputnik 将稀疏矩阵数据存储在共享内存中，并受限于共享内存的加载带宽。因此，Sputnik 采用了 ** 子 warp 分块** 和 ** 反向偏移内存对齐** 等优化来减轻带宽瓶颈，通过实现向量化内存加载来提升性能。
SparseRT 则将稀疏矩阵数据嵌入到指令缓存中，并作为指令操作数存储，因此无需上述优化。然而，Sputnik 在处理较大矩阵时不会受到指令获取瓶颈的影响，其性能也不会下降。

Sputnik 还对稀疏矩阵应用了 ** 行混排（row-swizzling）** 的预处理策略，以改善负载均衡。这一策略也可能对 SparseRT 有帮助，但原因不同。行混排将具有相似非零模式的行排在一起，如果相邻的稀疏矩阵行在相同列位置上有非零元素，则能减少稠密矩阵内存加载。在深度学习推理中，对稀疏权重进行预处理的成本可以通过后续所有推理请求进行有效摊销。我们目前正在探索预处理策略，以进一步提高 SparseRT 的性能。我们没有将 SparseRT 与 ASpT [24] 和 ** MergeSpMM** [45] 进行对比，因为这些方法在 Sputnik 的研究中已经被证明在深度学习 SpMM 问题上表现不佳 [15]。ASpT 和 MergeSpMM 主要优化的是科学计算中的 SpMM 工作负载，在这些场景下，稀疏矩阵通常非常大且高度稀疏，而稠密矩阵通常是“高且窄”（列数固定且较少）。事实上，ASpT 和 MergeSpMM 的实现都假设稠密矩阵有 32 或 128 列。然而，在深度学习中，稀疏矩阵可能比稠密矩阵小，而且其稀疏度通常远低于科学计算应用中的水平。此外，稠密矩阵的列数没有固定限制。此外，常见剪枝技术（如基于权重大小的剪枝）产生的稀疏模式通常较为均匀，与科学计算中的幂律模式或块状模式不同。这使得我们在大多数稀疏矩阵上的静态负载均衡策略效果不显著，也削弱了 ASpT 这类方法的优势，因为它们旨在利用稀疏矩阵不同区域的稀疏模式。然而，类似于 Sputnik 的行混排策略，ASpT 中提出的某些有趣的预处理策略也可能对 SparseRT 有益 [27]。 SpMM 可用于深度学习中的 稀疏 1x1 卷积 。此外，一些深度神经网络（如 ResNet-50 ）还大量使用 3x3 卷积 。近年来，有多个项目尝试加速稀疏 3x3 卷积，例如在 CPU 上的 SkimCaffe 和 ** Tiramisu** 以及在 GPU 上的 ** Escort** [4, 6, 33]。SparseRT 采用了“虚拟”密集矩阵的方法，将 ** im2col** 转换与 SpMM 内核融合，类似于 SkimCaffe 和 Tiramisu [4, 33]。 Escort 选择了一种直接稀疏卷积的方法，没有将卷积问题转化为隐式 GeMM，而是使用经典的 ** 7 层循环卷积算法**。在多个稀疏卷积问题中，Escort 的性能比 im2col + cuBLAS GeMM 快 ** 2-3 倍** [6]。然而，最新的 ** cuDNN** 库通过使用 ** Winograd 算法** 等优化，可以比 im2col + cuBLAS GeMM 快数倍。例如，在本文列出的四个问题上，cuDNN 的 Winograd 卷积比 cuDNN 的隐式 GeMM 卷积快 ** 2-4 倍**。因此，我们在本文中只将 ** SparseRT** 的性能与 cuDNN 进行对比，而不与 Escort 进行对比。然而，本研究和 Escort 在理念上有相似之处：两者都认识到问题的 内存瓶颈 。Escort 通过将稀疏矩阵和稠密矩阵存储在不同形式的片上数据缓存中来减轻内存瓶颈，而 SparseRT 则将稀疏矩阵存储在 指令缓存 和 ** 常量缓存** 中，完全避免了对片上数据缓存的依赖。此外，直接稀疏卷积的方法也旨在消除 im2col 转换的开销。我们表明，通过采用 [33] 提出的“虚拟”密集矩阵技术，我们可以高效地将 ** im2col** 转换与 SpMM 融合，并保持良好的性能。

6. Discussion and Conclusion

此外，需要注意的是，本研究只针对神经网络中的 矩阵乘法 和 ** 卷积** 进行优化。现代 DNN 的性能瓶颈往往在其他操作上，如 ** softmax** 和 ** 自注意力机制**。目前，SparseRT 不支持这些操作，因为即使在剪枝后的神经网络中，它们通常也不是以稀疏方式完成的。例如，在 ** Transformer 网络** 中，虽然生成查询和键向量的权重矩阵可以被剪枝，但生成的查询和键向量本身仍然是稠密的，因此 ** 自注意力机制** 仍然是一个稠密操作。我们期待未来的神经网络压缩和剪枝研究能够使这些操作也变得稀疏化。

很好的文章，实验部分做的很详细，和之前做实验的时候碰到的cuSPARSE跑起来速度甚至不如cuBLAS对应上了，它在神经网络这样的操作下面就是没有直接稠密硬算更快。可惜还是在Weight Sparsity上面做文章，runtime的Sparsity还是很难处理，对之后那个算子的工作应该没什么帮助。

SparseRT: Accelerating Unstructured Sparsity on GPUs for Deep Learning Inference