摘要: Transformer在序列长度方面的可扩展性限制重新引发了对在训练时可并行化的递归序列模型的兴趣。因此,许多新颖的递归架构被提出,例如 S4、Mamba 和 Aaren,这些模型在性能上达到了相当的水平。在本研究中,我们重新探讨了十多年前提出的传统递归神经网络(RNNs):LSTM(1997年)和GRU(2014年)。虽然这些模型因需要通过时间反向传播(BPTT)而训练速度较慢,但我们发现,通过移除其隐藏状态在输入、遗忘和更新门中的依赖,LSTM 和 GRU 不再需要进行 BPTT,从而可以高效地并行训练。基于此,我们提出了精简版本(minLSTMs 和 minGRUs),它们具有以下特点:1. ** 显著减少参数数量**,相比传统版本更加轻量化;2. ** 在训练时完全可并行化**,在长度为512的序列上训练速度提高了175倍。最后,我们展示了这些简化版的旧RNN模型在实验性能上与近期的序列模型表现相当。
1. Intro
基于Transformer的模型计算复杂度在token length上都是平方增长的,限制了scale up,所以最近人们开始重新关注具有以下特点的模型:
- 训练时消耗的内存和token length成线性关系
- 推理时消耗常量内存
最近流行的Mamba、RWKV以及Aaren,都采用了Parallel Prefix Scan Algorithm。这篇文章重新审视之前的LSTM和GRU,他们被时代抛弃的主要原因就是训练时只能通过BPTT,速度太慢。
2. Background
2.1. LSTM
其中, 表示向量的按元素乘法 ,是当前时间步, 是输出的隐藏状态, 是 与 的拼接, 是隐藏状态的维度, 是在序列中维护信息的细胞状态 , 是候选细胞状态。LSTM 的输入门 决定了从候选细胞状态中添加多少新信息,** 遗忘门** 确定要丢弃多少现有细胞状态中的信息,而** 输出门** 控制了从细胞状态输出哪些信息。激活函数 和 用于缩放,确保输出不会发生爆炸或消失。
总参数量。
2.2. GRU
其中,是候选隐藏状态,代表隐藏状态的潜在新值。GRU 将 LSTM 的输入门和遗忘门合并为一个更新门 ,该门控制了多少过去的信息得以保留(即 ),以及从候选隐藏状态中添加多少新信息(即)。此外,GRU 省略了 LSTM 的输出门,并引入了** 重置门**,该门决定了计算候选隐藏状态时应使用多少过去的信息。
减少了参数量,为。
2.3. Parallel Scan
为了替换Transformer提出的大部分RNN or RNN like算法都采用了prefix scan algorithm。
prefix scan algorithm:
并行扫描算法是一种并行计算方法,利用结合性操作符 (如加法和乘法),从 N 个顺序数据点计算出 N 个前缀计算结果。具体而言,该算法从输入数据 高效地计算出。
特别地,我们可以使用并行扫描算法高效计算如下形式的函数:
该方法的输入为 和 ,并通过并行扫描计算出。
3. Methodology
上面的公式可以拓展到向量形式:
可以看到LSTM和GRU里面有长得比较类似的模式。本文简化了RNN,移除输出范围的限制,并且确保在时间维度上是无关的,描述了miniGRU和miniLSTM。
3.1. A minimal GRU: miniGRU
3.1.1. Step 1: Drop previous hidden state dependencies from gates
GRU:
依赖于上一时刻,并且无法去除这种依赖,所以修改为:
3.1.2. Step 2: Drop range restriction of candidate states
原来的函数是帮助裁剪隐藏状态,但是现在只和自己相关之后不需要做这样的裁剪。
3.1.3. miniGRU
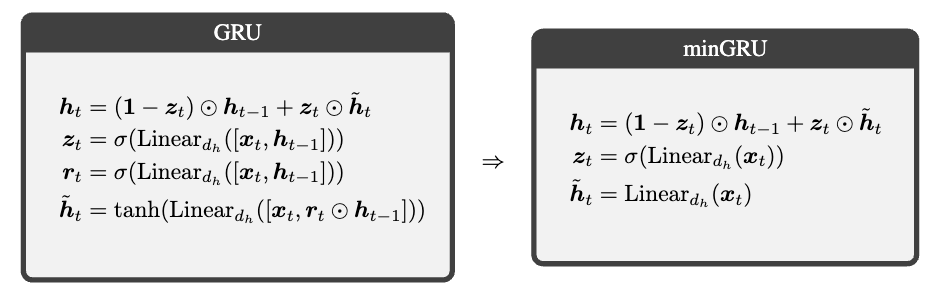
参数从下降到
3.2. A Minimal LSTM: minLSTM
3.2.1. Step 1: Drop previous hidden state dependencies from gates
3.2.2. Step 2: Drop range restriction of candidate states
3.2.3. Step 3: Ensure output is time-independent in scale
对遗忘gate和input gate做归一化,并且需要保证它们time independent。
3.2.4. minLSTM

参数从下降到,并且支持并行扫描训练速度很快。
4. Were RNNs All We Needed?
4.1. Minimal LSTMs and GRUs are very efficient
传统的RNN用BPTT的训练效率相当低。min系列的新RNN可以通过并行扫描方法进行并行计算,效率更高。文章重点对比的目标是Mamba,batch size=64.
Runtime & Memory:
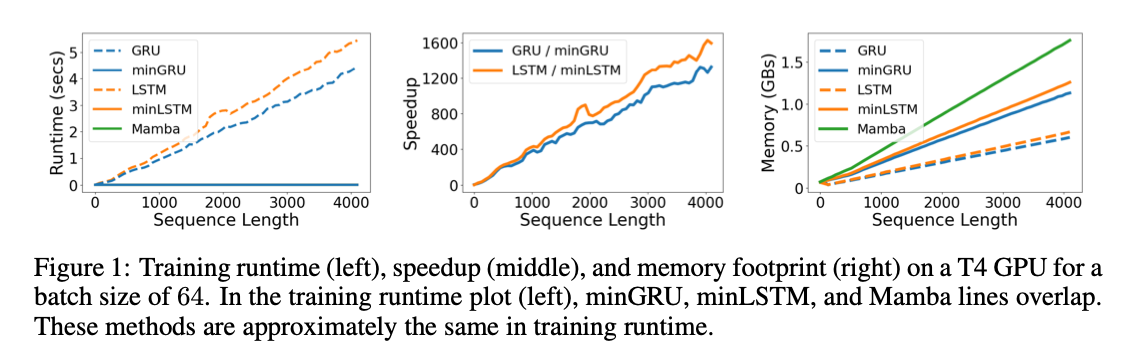
和sequence length基本是线性的了。
Other Tasks:
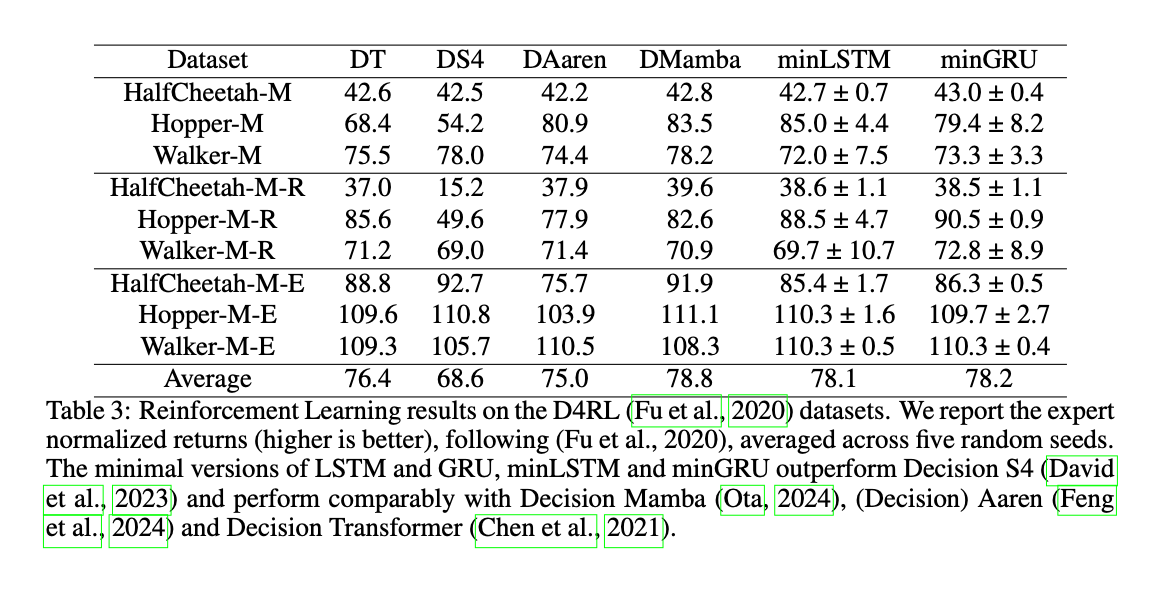
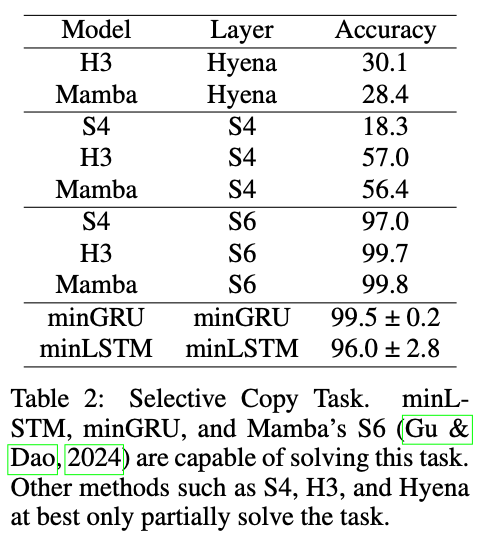
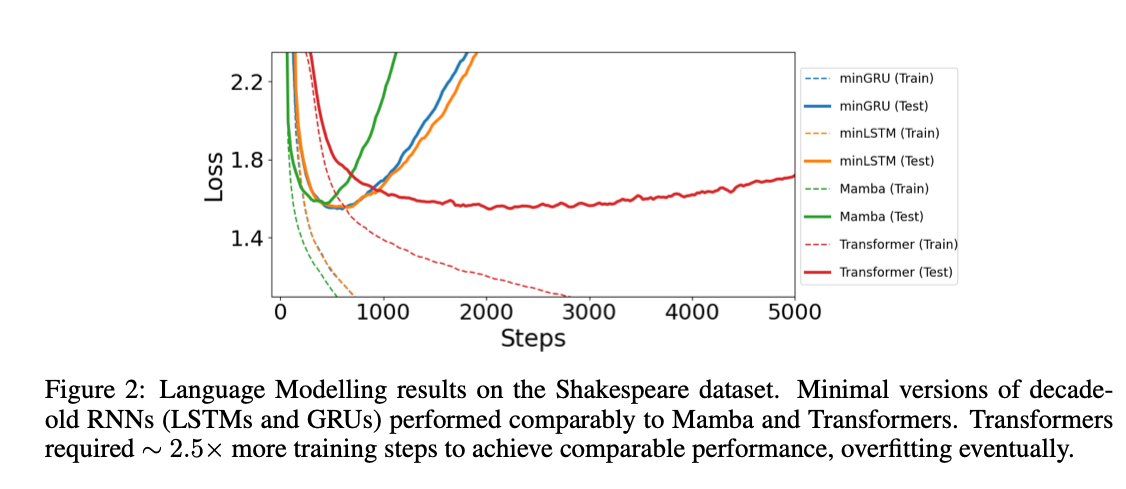
剩下的没有什么好讲的了,感觉实验太toy了,正大光明说就用了一张P100一张T4,感觉有点抽象。而且去掉了Hidden Dim之后还管自己叫RNN也有点奇怪。