摘要： 脉冲神经网络（Spiking Neural Networks，SNN）是一类受大脑神经机理启发的模型，可在神经形态硬件上以低能耗实现。然而，现有的直接训练方法通常将 SNN 限定在固定的时间步长下运行。这种“时间步长刚性”带来两大问题：1）难以在无需时钟的全事件驱动芯片上部署；2）无法根据动态推理时间步长在能耗与性能之间灵活取舍。本研究首先验证了训练在多种时间步长下均能泛化的 SNN 的可行性；随后提出了一种提升时间灵活性的全新方法——混合时间步长训练（Mixed Time-step Training, MTT）。在 MTT 的每一次迭代中，我们为网络的不同阶段随机分配时间步长，并通过通信模块在各阶段间传递脉冲。训练完成后，权重可直接用于带时钟驱动或纯事件驱动的平台。实验表明，MTT 训练的模型具有显著的时间灵活性：1. 在事件驱动与时钟驱动两类部署场景下均表现友好——在 N-MNIST 上几乎无损失，在 CIFAR10-DVS 上相较标准方法精度提升 10.1%；2. 提升了网络的泛化能力，接近当前最佳水平（SOTA）。据我们所知，这是首次报道大规模 SNN 在全事件驱动场景下部署并取得优异结果的工作。代码已开放，地址：https://github.com/brain-intelligence-lab/temporal_flexibility_in_SNN

1. Intro

之前的训练方法经常遇到问题：在固定的T上做训练，导致得到的SNN只在这个T上表现好，而对其他的T表现很差，导致：

无法灵活调整Timestep做elastic inference
在fully event driven chip上部署会有问题，因为在这种无时钟的芯片上根本就没有timestep这种概念

为了解决这个问题提出以下流程：

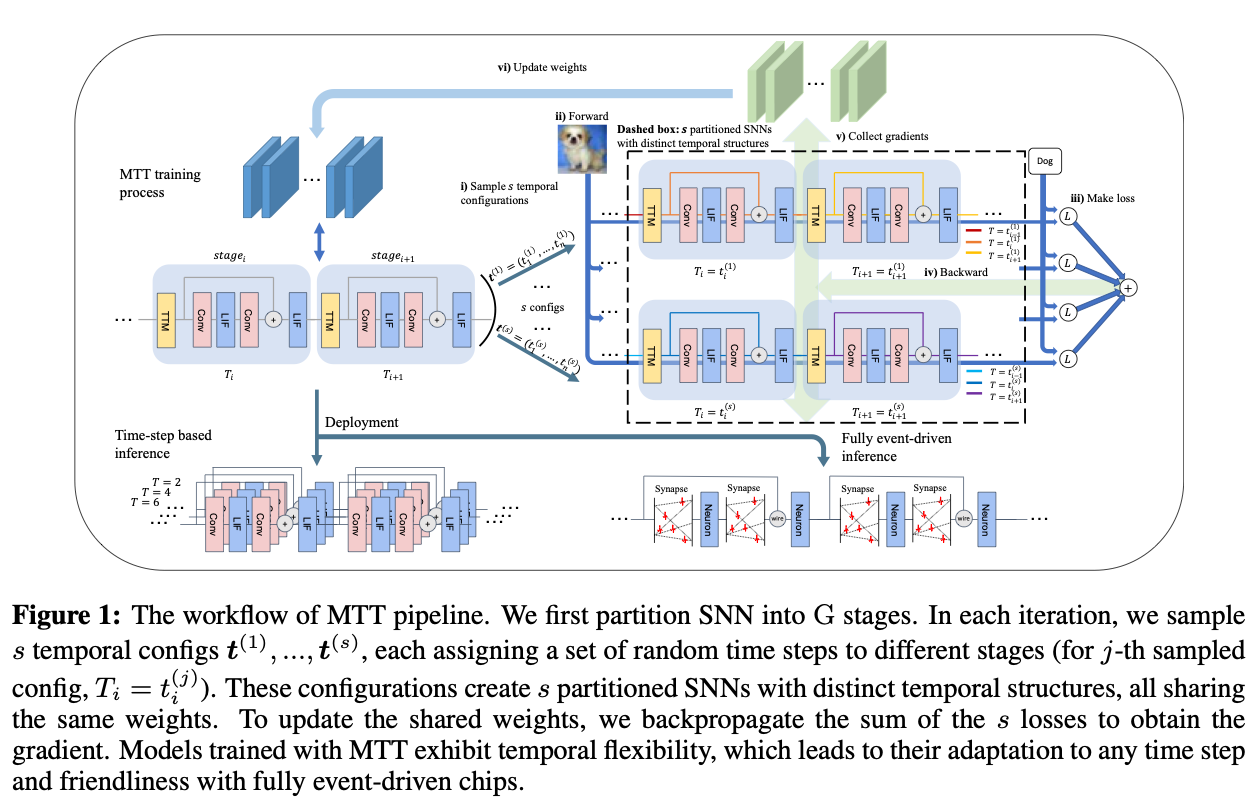
把SNN划分为G个阶段
每个epoch中，抽取s个Timestep设置 $t^{(1)}, ..., t^{(s)}$ ，给不同的阶段配置不同的timestep
将 $s$ 个子网络共享权重，训练的时候把loss求和然后反传，更新共享权重

Direct Training, Conversion, Dynamic Inference Time Step, Fully Event-driven Neuromorphic Chips，基本讲的就是那几个东西了。

3. Preliminaries

3.1. Spiking Neuron Model

LIF

3.2. Time-stepped Simulation, Clock-driven LIF/IF Model And Hardware

\begin{align*} v(t+dt)&=\tau u(t)+I(t)\\ s(t+dt)&=\mathcal{O}[v(t+dt)-V_{th}]\\ u(t+dt)&=s(t+dt)R(v(t+dt))+[1-s(t+dt)]v(t+dt) \end{align*}

文章中的 $V_{thr}=1, \tau=0.5$ 。

3.3. Event-based Simulation, Event-driven LIF/IF Model And Hardware

\begin{align*} v(t_i) &= e^{\frac{t_i-t_{i-1}}{\tau_0}}\,u(t_{i-1})+I(t_i) \\ s(t_i) &= \Theta\!\bigl[v(t_i)-V_{\text{th}}\bigr]\\ u(t_i) &= s(t_i)R\!\bigl(v(t_i)\bigr)+\bigl[1-s(t_i)\bigr]v(t_i)\end{align*}

这种连续形式很难训练，基本上是timestep训练然后期待基于事件能推理。

3.4. Surrogate Gradient

\frac{\partial s(t)}{\partial v(t)}\approx \frac{1}{h^2}\max(0, h-|V_{th}-v(t)|)

4. Methodology

4.1. Identifying Temporal Inflexibility and Potential Solution

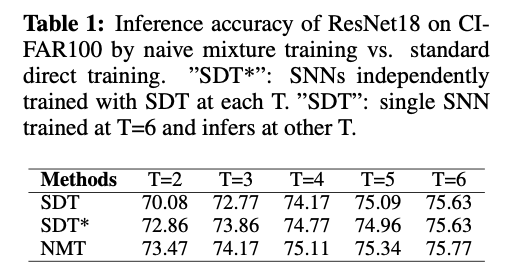
为展示该局限，我们用 ResNet-18 在 CIFAR-100 数据集上做实验。先在 T = 6 训练一套 SNN，然后在 5 个不同时间步上测试其准确率（Tab. 1 中 “SDT”）。现实部署往往与训练用的时间结构不同——例如全事件驱动芯片本身没有显式时间步；又如时钟驱动系统可能为了能耗-性能折衷而动态调整 T。时间刚性会阻碍模型在部署端的泛化。为缓解时间刚性，我们提出一个直观的方法：朴素混合训练（Naive Mixture Training，NMT） ：每次迭代从预设集合 {1, 2, … , 6} 随机抽 3 个时间步 $T_i$ ，依次做 3 次前向，最后一次性反传更新参数。Tab. 1 显示，单一 NMT 模型已能达到分别用 SDT 在各 T 上训练（标记为 SDT*）的水准，说明 NMT 有效削弱了时间刚性，使模型跨时间步具备时间灵活性（temporal flexibility） 。

4.2. Analysis on Naive Mixture Training

Temporal Flexibility: SDT 只在单一 T 上优化，容易过拟合该时间结构；NMT 同时训练 6 种结构，迫使网络学会在不同 T 上保持性能。
Event-driven Friendliness: 事件驱动可看作 “T → ∞” 的极限。NMT 训练出的网络已对多 T 稳定，更易迁移到真正的全事件芯片。
Network Generalization: 迭代中随机切换 T 类似于一种新的 dropout；若梯度把模型从局部极小拉出，最终收敛到更平坦的极小域，因而在小 T 时尤显著提升。

4.3. Mixed Timestep Training

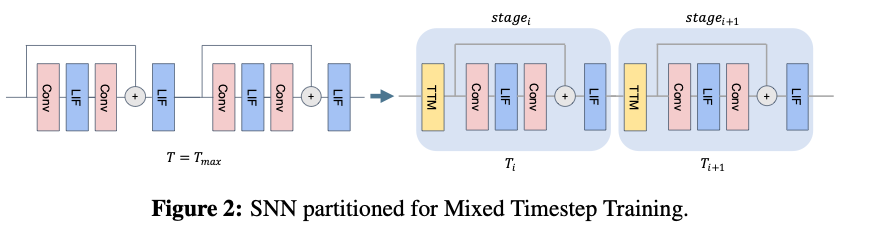
4.3.1. Network Partitioning

将网络划分成 $\mathcal{G}$ 个阶段，一次前向推理总共耗时

\mathbb{t}=(t_1, ..., t_G), t_i\in [T_{min}, T_{max}]

4.3.2. Temporal Transformation Module

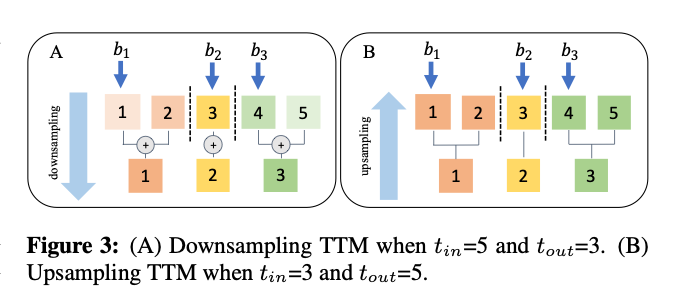
因为网络被划分之后每个模块的timestep可能不同，因此需要用一个额外的模块对齐。downsampling的时候类似pooling，upsampling的时候采用：

b_i=\lfloor\frac{(i-1)\cdot l}{k}-\epsilon\rceil+1, i\in\{1, .., k\}

4.3.3. Mixed Timestep Training

\mathcal{L}_{\text{MTT}}^{\text{overall}}=\;\sum_{k=1}^{N}\;\sum_{\mathbf{t}\,\in\,\{T_{\min},\dots,T_{\max}\}^{G}}\mathcal{L}\!\bigl(S_{P}(x_k,\mathbf{t}),\;y_k\bigr).

但组合空间过大，实际在每次迭代随机采样s 个，累加损失后反传。

这样训BN的波动太大容易掉点，所以直接用 $T_{\max}$ 的统计量处理BN。

4.4. Tests on Fully Event-driven Scenarios

选用Synsense Speck2e，全事件驱动、超低功耗。芯片规模有限，无法容纳大 backbone，于是编写了并行事件驱动模拟器，在小数据集上与真芯片对齐，再用来跑大数据集。

新的指标Spike Difference:

\mathrm{SD}\!\left(\mathbf{s}_0,\mathbf{s}\right)=\;\frac{ \sum_{i=0}^{N_f-1} \bigl|\,s_0[i] - s[i]\,\bigr|}{\sum_{i=0}^{N_f-1} s_0[i]}\;

衡量芯片和模拟器的输出差异。

5. Experiments

CIFAR10. CIFAR100, ImageNet, CIFAR10-DVS, N-Caltech101。网络结构包括ResNet18, Resnet19, ResNet34, VGG.

5.1. Validation Experiments

Temporal Flexibility Across Time Steps，实验证明掉点少，尤其是DVS这样的数据，配合early stop。

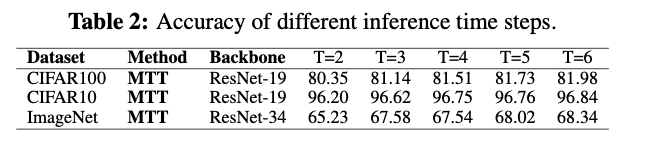
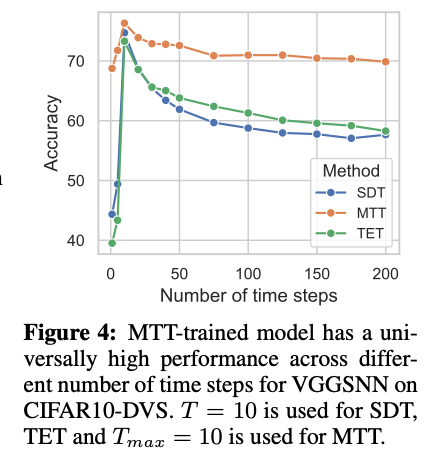
Event-driven Friendliness, 在MNIST跑的，发现如果用Clock-driven训练出来的模型，评估得到的spike数量和在芯片上跑的spike数量相差30%，而使用MTT训练出来的模型在模拟器上跑和在芯片上跑的spike数量只相差3%。

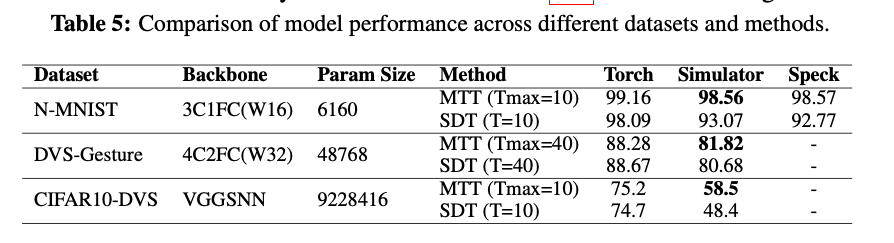
由于面向芯片部署，模型不含偏置；Speck 等全事件芯片省去了逐时间步加偏置等操作，极致节能，适合“永远在线”场景。

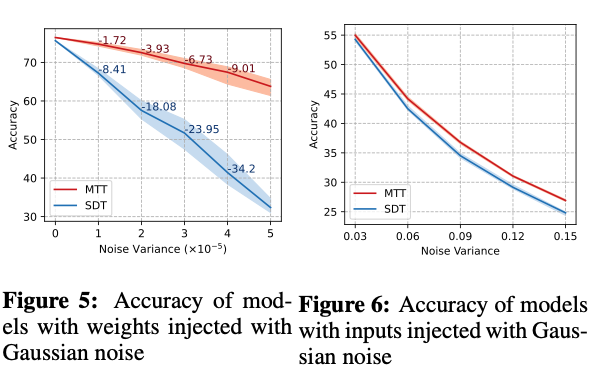
做adversary attack更加稳定。

5.2. Ablation Study

MTT 相较 NMT 的核心改进是把网络划分为时间步不同的多个阶段。我们在 CIFAR-100 上以 ResNet-18 为例，验证分段粒度的作用。定义粒度常数 g 为“每个阶段包含的残差块数”。在 ResNet-18 中共有 8 个块，因此 NMT 可视为 g=8 的特殊情况。实验分别以 g=1,2,4,8 训练四个 MTT-SNN，并用 SDT 训练一组对照；然后在 T=2,3,4,5,6 上测试准确率。结果：随着 g 减小（阶段数增多，时间结构更丰富），整体性能稳步提升，验证了网络分段的有效性。

6. Conclusion

本文首先指出了主流 SNN 训练范式隐含的副作用——“时间刚性” ：GPU 上训练的模型在部署到神经形态硬件时，若时间结构不一致，性能会大幅下降。针对这一痛点，我们提出了混合时间步训练（MTT） ：

通过“网络分段 + 随机时间步配置”在训练阶段引入多样化的时间结构；
显著提升模型的时间灵活性 与事件驱动兼容性 ；
在 GPU、真实芯片（Synsense Speck）和事件驱动模拟器的大量实验中验证其有效性；
同时保持与最先进方法相当的准确率。

MTT 的思想还能迁移到其他训练场景，例如随机累积输入帧或在在线学习中动态调整时间步。我们相信，MTT 为“几乎零损失”的事件驱动部署指明了方向，也期待它能激发更多针对 SNN 部署问题的研究。

讲了Elastic Inference的问题，虽然做的方法有点神秘。感觉大家逐渐意识到SNN具有的一些ANN没有的特性了。

Temporal Flexibility in Spiking Neural Networks: Towards Generalization Across Time Steps and Deployment Friendliness