摘要： 脉冲神经网络因其能效高和生物可解释性强而备受关注，它们通过脉冲驱动计算利用 0-1 激活稀疏性。现有 SNN 加速器虽然借助这种稀疏性跳过零计算，但往往忽视了二值激活所固有的独特分布模式。本研究发现脉冲激活中存在可用于降低 SNN 模型大量计算量的特定模式。基于此，我们提出了一种新的基于模式的分层稀疏框架 Phi，以优化计算。Phi 引入两级稀疏层次：第一级 通过预定义模式表示激活，实现向量级稀疏，可在离线阶段与权重预计算，从而显著减少大部分运行时计算；第二级 通过补充第一级矩阵，实现元素级稀疏，利用高度稀疏的矩阵在保持准确率的同时进一步减少计算。我们采用算法-硬件协同设计：在算法层面，使用基于 k-means 的模式选择方法提取代表性模式，并引入模式感知微调技术以增强第二级稀疏性；在架构层面，设计了专用硬件架构 Phi，可在运行时高效处理 Phi 的两级稀疏。大量实验表明，与最先进的 SNN 加速器相比，Phi 在速度上提升 3.45×，能效提升 4.93×，充分证明了该框架在优化 SNN 计算方面的有效性。

1. Intro

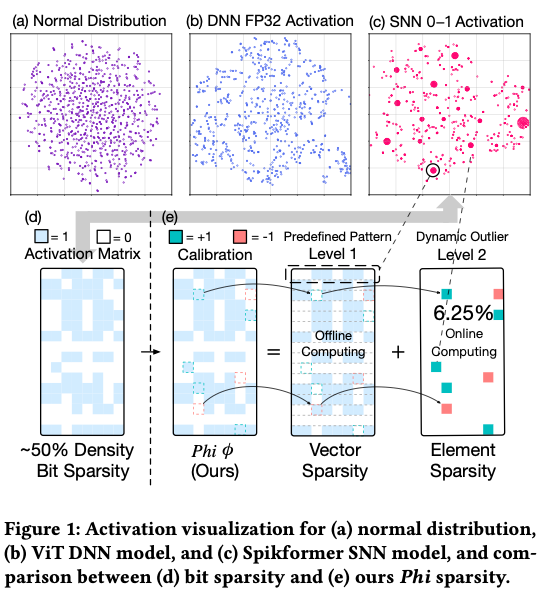
传统DNN加速器有一些很好玩的研究稀疏模式的工作，比如JPEG- ACT发现feature map和图片本身的形状是有相似性的，因此可以考虑使用JPEG压缩达到更高的压缩率。如下图所示，SNN的激活值也具有一定的稀疏模式。

Contribution:

• 我们提出了一种新颖的分层稀疏性框架 Phi，结合向量级和元素级稀疏，大幅减少 SNN 计算量
• 我们开发了基于 k-means 的模式选择和模式感知微调算法，在最大化稀疏效果的同时将离群值最小化
• 我们设计了硬件架构 Phi，可以动态生成和处理两级稀疏性，应对存储开销和负载不均等挑战
• 大量实验表明，与最新的 SNN 加速器相比，Phi 在运行速度和能效方面分别提升了 3.45× 和 4.93×

2. Background and Motivation

2.1. SNN Background

现有 SNN 加速器通过跳过 0 元素的计算，并将完整的 MAC 操作简化为仅有累加的 AC 操作，从而实现了显著的能耗节省

2.2. SNN Accelerators

SpinalFlow 通过按时间步对脉冲激活进行排序并顺序处理，来跳过 SNN 激活中的零元素。

SATO 在每个时间步并行整合输入脉冲，并利用二进制加法-搜索树在无需累积膜电位的情况下生成输出脉冲。

PTB 同样采用并行方式处理比特稀疏性，引入了基于 systolic array 的架构，但它仍需处理大量无效的时间步。

Stellar 依赖 Few Spikes 神经元来提高激活稀疏性，并通过专门设计的数据流来利用该稀疏性。

Prosperity 提出了乘积稀疏性 （product sparsity）概念，通过重用之前的内积结果来提高比特稀疏度。

以往工作主要通过顺序或并行的方法优化比特稀疏性的处理，但它们忽视了稀疏激活中固有的模式结构。我们的 Phi 框架识别并利用了这些结构化模式，为提升 SNN 的计算效率开辟了新途径

2.3. Motivation

SNN 激活展现出比 DNN 激活更强的规律性 ，形成了清晰的簇状结构(图1）。

为有效捕获这些模式，我们将 0-1 激活矩阵按宽度分割成多个分区 （partition），定义每行中的 0/1 组合为一个模式 。图 1(c) 展示了许多激活行具有相同或相似的模式 。SNN 激活中的这种内在结构为架构和计算优化提供了新的契机。 虽然激活值在推理时是动态生成的，无法提前预测每个位置的 0/1，但统计分布表明某些激活模式会稳定地反复出现（只是位置有所不同）。通过预先识别这些模式，我们可以在离线阶段将它们与权值进行矩阵运算，预计算得到结果。在在线推理时，当某一激活行匹配预先识别的模式时，我们可以直接调用预计算结果，从而免去实时计算。

2.4. Challenges

2.4.1. Algorithmic Challenges

• runtime activation的不确定性
• pattern的复杂性

2.4.2. Hardware Challenges

• 对于预处理的结构化稀疏（L1）用了类似LUT的模式，访存瓶颈严重
• 对于非结构化稀疏（L2）会影响计算阵列的利用率

3. Pattern-based Hierarchical Sparsity

3.1. Phi Sparsity definition

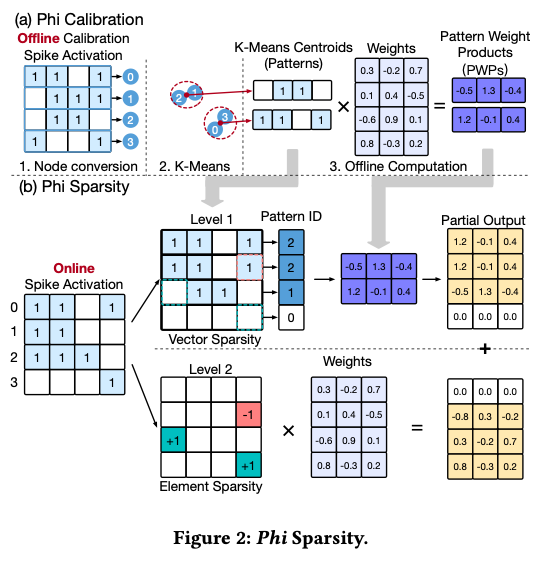
Phi 稀疏性将激活矩阵分解为两级稀疏矩阵：第一级由预定义模式组成，在离线预计算后提供结构化的向量级稀疏 ；相反，第二级包含第一级未覆盖的元素，并以非结构化的元素级稀疏 形式存在，需要在线处理。

模式识别是 Phi 稀疏性的基石，我们基于激活行之间的相似性来选取模式。具体而言，激活行长度越长，其可能组合指数级增长，频繁出现相同模式的可能性下降。为了解决这一问题，我们沿 K 维度将激活矩阵划分为大小为 k 的较小分区，每个分区独立识别模式。通过这样的划分，我们降低了模式搜索的复杂度，提高了模式出现频率。

当某行与某模式相似但并非完全相同时，我们在第二级稀疏中引入双向校正机制 来处理差异。该机制包含两种情形：

1. “1” 转 “0” 不匹配 ：当激活中某位为1但对应模式为0时（例如图 2(b) 中，行2 = 1110，而模式1 = 0110），我们在第二级矩阵的相应位置设置一个 1 作为校正（例如补上 1000）。
2. “0” 转 “1” 不匹配 ：当激活中某位为0但对应模式为1时（例如行1 = 1100，而模式2 = 1101），我们在相应位置设置一个 -1 进行校正（例如补上 000-1）。

3.2. Phi Sparsity Calibration Stage

实验证明，只需少量训练数据就足以代表测试数据的分布。这一发现使我们能够在一个静态的校准数据集上执行模式校准，并将结果有效应用到运行时。这也意味着针对不同模型、数据集和层，我们可以分别选取独立的模式，以捕获各自的局部分布特征。

找到能让某给定激活矩阵第二级稀疏度最大的最优模式集，本质上是一个 NP-hard 问题。然而，通过对激活分布的研究，我们发现了一些启发式方法，在保持高效果的同时显著简化了模式选择过程。基于图 1(c) 中观察到的簇状行为，我们发现每个簇的中心点 自然可以作为理想模式。这种方法有两个主要优点：

• 每个属于某簇的激活行都可以自然地被赋予该簇代表的中心模式。由于每个簇中包含大量激活行，大部分行都能被赋予某个模式。
• 选择每个簇的中心作为模式，可以最小化模式与属于该模式的激活行之间的累计距离，从而最大化第二级稀疏度 。

3.3. Pattern-aware Fine-tuning

对L2稀疏的进一步优化，引入有损的算法取得更高的性能。在训好的SNN上finetune，鼓励模型的脉冲更加接近于L1里面的模式，这样能进一步提高L2的稀疏度。

3.4. Phi Framework Overall Workflow

Phi 框架以训练好的 SNN 模型及其训练数据集为输入。首先，对一小部分训练数据执行 Phi 校准，以导出针对该模型和数据集的模式。接下来，对预训练模型应用微调，使其激活进一步与校准模式对齐。然后，将校准得到的模式和模型权重送入 Phi 硬件架构，在硬件上生成并处理两级稀疏性。需要注意的是，PAFT 并非强制步骤，如果更关注精度，PAFT 可以跳过。

4. Phi Architecture Design

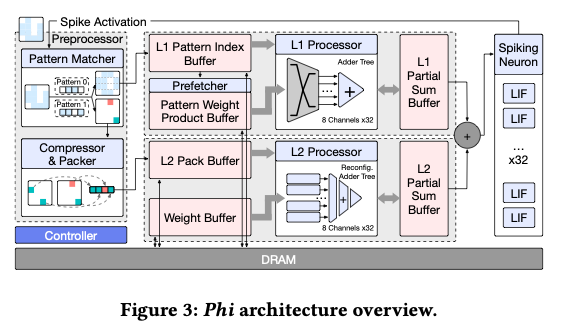
4.1. Overview

• Tiling Strategy，优先遍历K维度，“通过分块策略，每轮计算会产生一个输出分块，该分块直接送入脉冲神经元阵列进行处理，生成脉冲激活，并立即反馈到预处理器用于下一层的激活处理。这样形成了矩阵乘法、脉冲神经元计算和预处理三者高度重叠的流水执行。这种流水线有效地消除了预处理的额外开销，因为这些操作被无缝集成到了主要计算流中，而不再作为独立的顺序步骤“
• Preprocessor，算上面两级稀疏的，“预处理器包含一个模式匹配器（pattern matcher），用于将每一行激活与预定义模式集进行比较。对于每一行激活，模式匹配器选出模式集中最匹配的模式作为第一级的模式，同时生成对应的第二级稀疏信息。为缓解第二级稀疏的不规则性带来的挑战（如负载不平衡和不规则内存访问），预处理器中的压缩器（compressor）和封装器（packer）模块会将多个第二级稀疏行整合到一个打包结构中，并按优化的顺序排列，以提高数据密度和访问效率。 ”
• L1 Processor，LUT，prefetcher；
• L2 Processor，“虽然 L1 和 L2 处理器能够独立并行运行，但在每个输出分块计算完成时需要进行同步。我们的设计精心平衡了两个处理器的计算负载，将干扰降至最低，同时最大化总体吞吐率”
• Spiking Neuron Array，聚合L1 L2结果然后做LIF Neuron的计算

4.2. Preprocessor

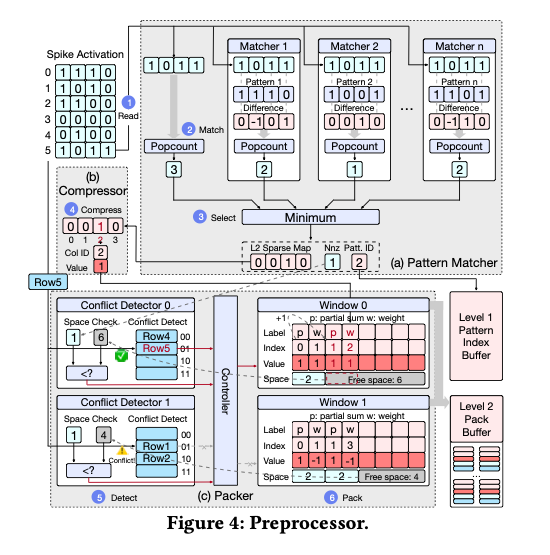
4.2.1. Phi Pattern Matcher

大概是逐行处理找让L2稀疏度最大的L1 pattern fit。

4.2.2. Level 2 sparse preprocessing

Row major的压缩策略，设计了一种新的数据格式；

4.3. L2 Processor

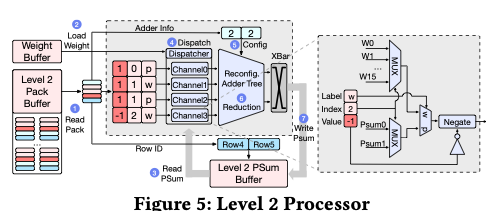
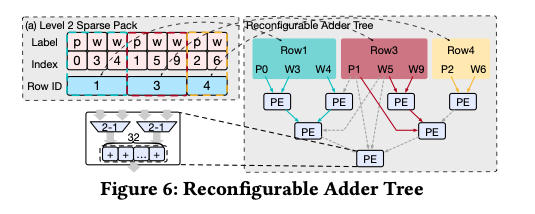
我们的 L2 处理器在高稀疏条件下实现了 M、N、K 三个维度上的全方位并行：沿 M 和 K 维度，通过并行处理包内多个单元，实现对多行（M 维）和单行内不同单元（K 维）的同时处理；沿 N 维度，通过对权重和部分和行执行 SIMD 加法实现并行。这种多维并行结合高效的数据组织和可重构架构，成功应对了工作负载不均的挑战，使 L2 稀疏矩阵的乘法在硬件上达到高性能和高利用率。

4.4. L1 Processor

5. Evaluation

5.1. Methodology

在Spiking VGG, ResNet, Spikeformer, SDT, SpikeBERT, SpikingBERT上，跑CIFAR10, CIFAR100, CIFAR10-DVS, SST-2, MNLI。

用模拟器做的，28nm评估面积和能耗。

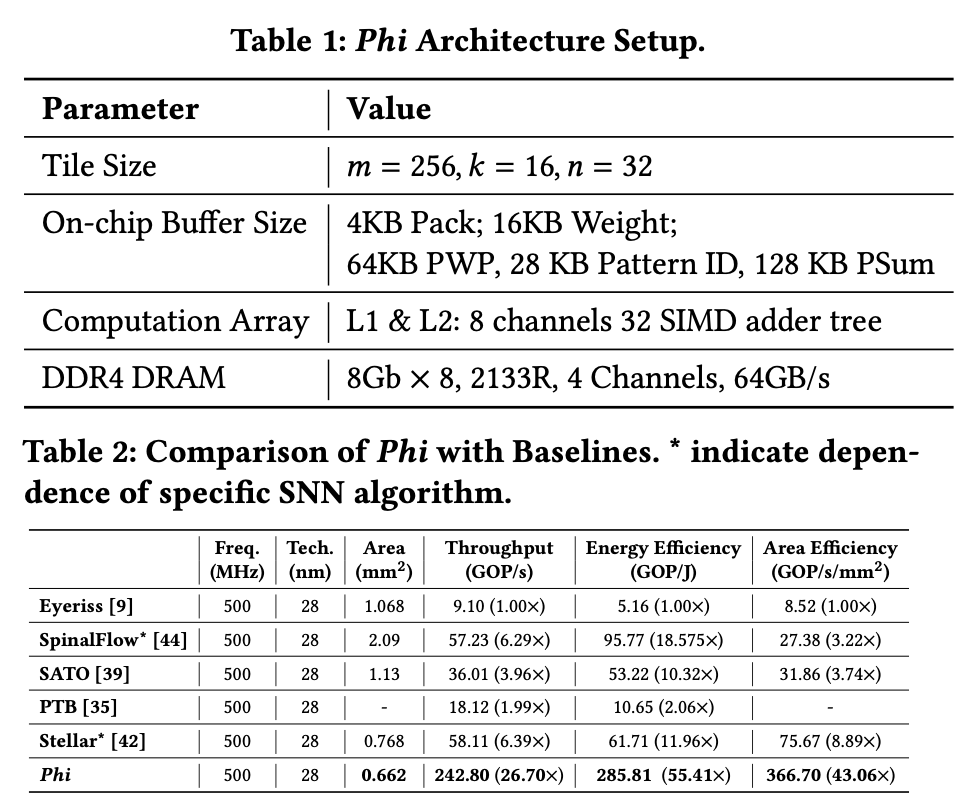
5.2. Design Space Exploration

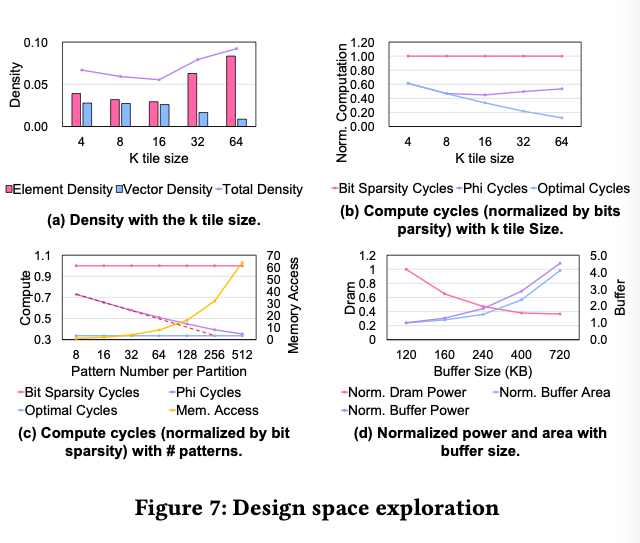
5.2.1. Tile Size of K

可以发现稀疏度决定了计算量大小，而上面的setting中$k=16$的稀疏度最高。

5.2.2. Number of Patterns

pattern多计算少但是存储/访存问题更大。

5.2.3. Buffer Size

5.3. Phi Performance and Energy

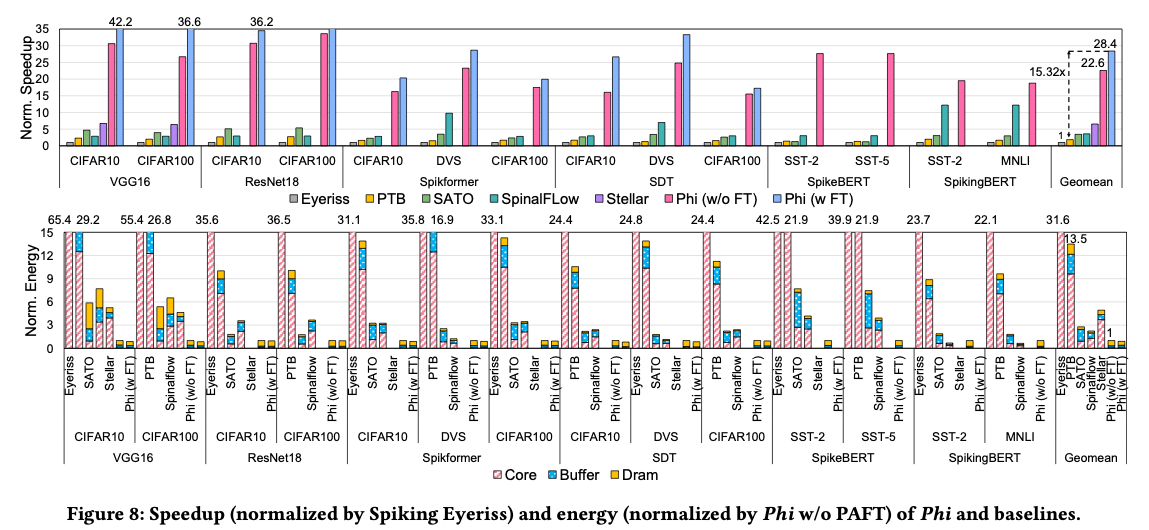
5.3.1. Performance

5.3.2. Energy

需要说明的是，由于以减少计算为代价引入了一定额外的内存访问，我们的 DRAM 能耗并没有显著降低

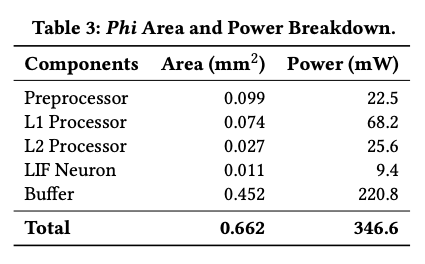
5.3.3. Area and Power Breakdown

5.4. Pattern-aware Fine-tuning Analysis

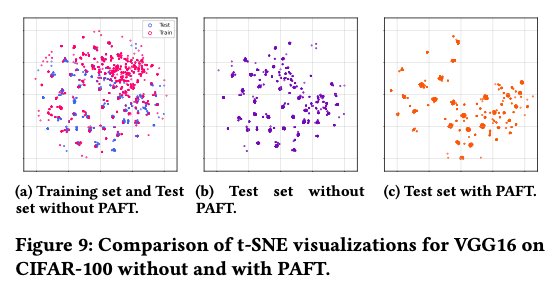
大概意思是说，test set和training set的稀疏模式分布是相似的，而训完之后更加集中在已经有的模式附近了。

5.4.1. Improvement Analysis

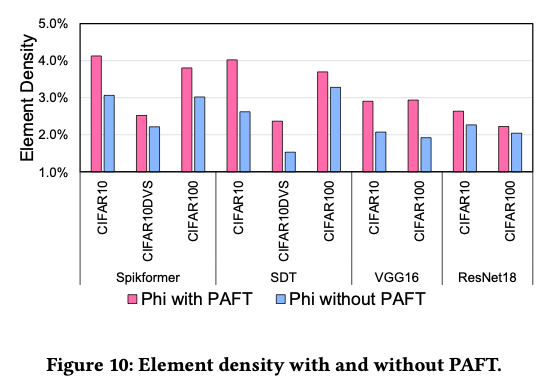
这些减少意味着更多的激活被模式精确表示，第二级需要处理的离群项更少，计算效率相应提高。

5.4.2. Accuracy Results

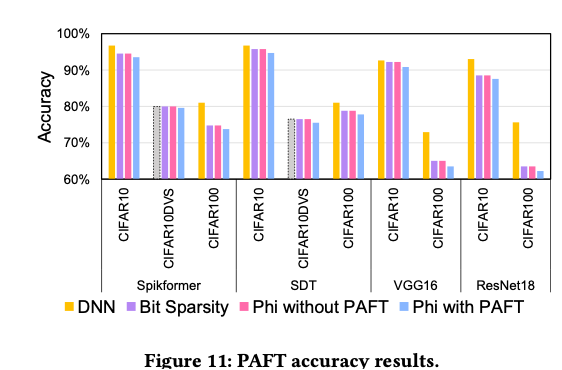
5.5. Memory Traffic Reduction

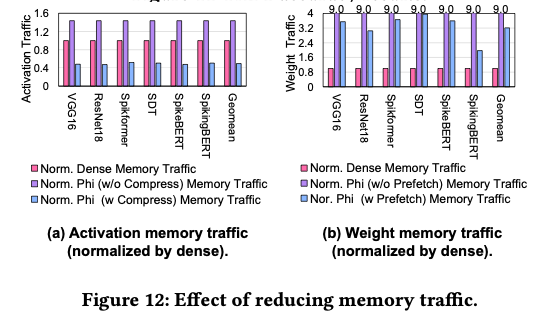
5.6. Phi Generalizability Analysis

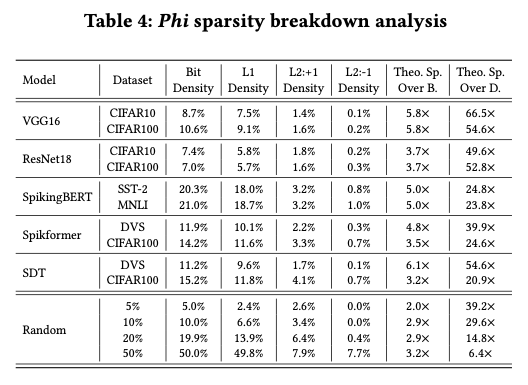
6. Discussion

6.1. Benefit and Cost of Phi Preprocessing

通过对所有 SNN 模型的实验数据进行统计，我们发现：预处理所消耗的能量仅相当于减少的累加运算能量的 1/75.5。换言之，由于稀疏度提升减少的计算量带来的能量节省是预处理开销的 75.5 倍。由此可见，Phi 实现了一个极佳的权衡：预处理的少许代价换来了计算的大幅减少。

6.2. Relationship with Sparsity and Quantization in DNNs

稀疏性。  大量研究致力于在 DNN 中利用稀疏性提升计算效率。Phi 从中获得了灵感，但独辟蹊径地利用了 SNN 的二值特性，取得了更大的性能提升=。例如，CGNet通过结构化剪枝裁剪不重要的通道，SIGMA跳过不结构化的零激活，但这些方法仅针对零元素进行优化。相反，Phi 利用基于模式的稀疏 ，借助 SNN 独特的二值属性，跳过了激活中大量与非零相关的计算。这使我们不仅跳过零值计算，还跳过了模式匹配下的重复计算，在原理上有别于传统 DNN 稀疏优化。 量化.  近期在 DNN 量化领域的进展（尤其是bit-slicing  方法）表明，Phi 的理念有望推广到更广泛的场景。Bit-slicing 将多比特整数矩阵分解为一组二进制矩阵，从而可以利用比特级稀疏 。已有一些工作利用了这种稀疏性：BBS通过对称性剪枝同时利用 1-bit 和 0-bit 的稀疏性，Transitive Array重用二进制矩阵中的先前结果以减少重复计算、增强比特级稀疏。Phi 专注于二进制矩阵处理，这一思想可以扩展到 bit-sliced DNN ，为利用比特级稀疏提供新的机会。 简而言之，Phi 的模式稀疏性理念与 DNN 中稀疏和量化技术存在共通之处，但更进一步地挖掘了 SNN 的二值特性。未来，我们希望将 Phi 的思想应用到 bit-slicing 的 DNN 上，进一步验证其在更广泛领域的价值。

7. Conclusion

本文提出了Phi ——一种新颖的分层稀疏框架，它利用 SNN 激活中的结构模式，生成向量级 和元素级 两级稀疏。我们通过算法—硬件协同设计解决了关键挑战：使用基于 k-means 的模式选择和模式感知微调优化算法，设计专用硬件高效地在线生成和处理两级稀疏。实验结果表明，该系统相比最新的 SNN 加速器实现了3.45× 的速度提升和4.93× 的能效提升。我们的工作展示了基于模式的分层稀疏性在推动 SNN 实用化方面的巨大潜力，同时也为探索 SNN 激活模式的内在规律及其在其他神经网络中的潜在应用开辟了新方向