摘要： 我们探讨了进化策略（ES）的使用，这是一类黑箱优化算法，作为流行的基于MDP的强化学习技术（如Q学习和策略梯度）的替代方案。在MuJoCo和Atari上的实验表明，ES是一种可行的解决策略，并且在可用CPU数量上具有极好的扩展性：通过使用一种基于公共随机数的新型通信策略，我们的ES实现只需要传递标量，使其能够扩展到超过一千个并行工作者。这使我们能够在10分钟内解决3D人形步态问题，并在经过一个小时的训练后，在大多数Atari游戏中获得竞争力结果。此外，我们强调了ES作为黑箱优化技术的几个优点：它对动作频率和延迟奖励不变，对极长时间范围具有容忍性，并且不需要时间折扣或价值函数近似。

1. Intro

强化学习中，除了给予马尔可夫链的RL方法，还有一类基于Black-Box Optimization的方法，在RL中通常称为“Direct Policy Search”直接策略搜索或者“Neuron Evolution”神经演化。

Contributions:

本文发现用Virtual Batch Normalization等各种重参数化的方法可以显著提高Evolution Strategy的稳定性；
Evolution Strategy具有高度并行性；
Evolution Strategy的数据利用率略逊于基于梯度的方法，但是不需要反向传播和reward function，计算量大幅度减少了；
Evolution Strategy学习到的数据的多样性相比于基于梯度的方法更加丰富；
Evolution Strategy具有很高的稳定性；

2. Evolution Strategy

ES是一类黑箱优化算法，每次迭代对一个参数向量种群进行扰动，评估目标函数，然后将得分最高的若干个个体进行重组，形成下一代群众，直到目标函数被充分优化。

Formulation：记 $F$ 是作用在参数 $\theta$ 上的目标函数，Natural Evolution Strategy用另一个参数向量 $\psi$ 来表示一个分布 $p_\psi(\theta)$ ，然后对期望 $\mathbb{E}_{\theta\sim p_\psi}F(\theta)$ 做随机梯度上升，不断改进 $\psi$ ，具体来说：

\nabla_\psi\mathbb{E}_{\theta\sim p_\psi}F(\theta)=\mathbb{E}_{\theta\sim p_\psi}[F(\theta)\nabla_\psi\log p_\psi(\theta)]

方法类似REINFORCE中的“score function”。

REINFORCE梯度：考虑轨迹 $\tau=(s_0, ..., s_T)$ 有Reward $R(\tau)=\sum_{t=0}^T\gamma^tr_t$ ，策略 $\pi(a|s)$ 给出动作分布，希望最大化 $J(\theta)=\mathbb{E}_{\tau\sim\pi_\theta}[R(\tau)]$

\begin{align*} \nabla_\theta J(\theta)&=\nabla_\theta\int p_\theta(\tau)R(\tau)d\tau\\ &=\int R(\tau)\nabla_\theta p_\theta(\tau)d\tau\\ &=\int R(\tau)p_\theta(\tau)\nabla_\theta\log p_\theta(\tau)d\tau\\ &=\mathbb{E}_{\tau\sim \pi_\theta}[R(\tau)\nabla_\theta\log p_\theta(\tau)] \end{align*}

则

\log p_\theta(\tau)=\sum_{t=0}^T(\log\pi_\theta(a_t|s_t)+\log P(s_{t+1}, a_t))

环境转移项 $P$ 直接忽略，则有：

\nabla_\theta J=\mathbb{E}[R(\tau)\sum^T_{t=0}\nabla_\theta \log\pi_\theta(a_t|s_t)]

假设 $p_\psi$ 是一个factored Gaussian，这个梯度估计也被称为同时扰动随机近似（simultaneous perturbation stochastic approximation）或者参数探索策略梯度（parameter-exploring policy gradients），以及零阶梯度估计（zero-order gradient estimation）。

本文中主要关注强化学习的场景 $F(\cdot)$ 被看作是环境提供的return， $\theta$ 是一个策略的参数。考虑到不能保证环境的梯度可导，为了保证可微性，令：

\mathbb{E}_{\theta\sim p_\psi}F(\theta)=\mathbb{E}_{\epsilon\sim \mathbb{N}(0, I)}F(\theta+\sigma\epsilon)

其中 $\sigma^2I$ 为固定协方差。换而言之，原目标 $F$ 已经经过了一次高斯模糊，摆脱了原环境中可能的不可微的性质。在此定义下，进一步改写 $\theta$ ：

\nabla_\theta\mathbb{E}_{\epsilon\sim\mathbb{N}(0,I)}F(\theta+\sigma\epsilon)=\frac{1}{\sigma}\mathbb{E}_{\epsilon\sim\mathbb{N}(0,I)}[F(\theta+\sigma\epsilon)\epsilon]

然后进行采样：

2.1. Scaling and parallelizing ES

ES很适合做并行，因为：

ES计算是一个episode一个episode做的，episode内部不存在通信，通信很少；
每个node只需要在每个episode传递一个scalar：考虑seed固定，则 $\theta\leftarrow\theta+\alpha\frac{1}{n\sigma}\sum^n_1F_i\epsilon_i$ 中 $\epsilon_k$ 可以自己算，只有 $F_i$ 需要从别的机器传过来；
没有reward function，不需要迭代更新跟当前的policy保持一致；

实践中，我们通常让每个节点在训练开始时各自实例化一大块高斯噪声，然后在每次迭代时从其中选取相应的子块来对参数进行扰动。这样虽然在严格意义上不同迭代间的扰动不是完全独立的，但实验中并未观察到什么不良影响。为了减小方差，我们采用对称采样（antithetic sampling），也称为镜像采样（mirrored sampling），即同时评估一对噪声向量 $\epsilon$ 和 $-\epsilon$ 。我们还对回报值进行排序变换（rank transformation）来实现”适应度整形”（fitness shaping）：用回报的排序替代原始标量回报，这样可以降低离群值的影响，并减少训练早期陷入局部最优的可能性。此外，我们在策略参数上使用权重衰减（weight decay）来防止参数量级膨胀。与 Rank Transformation文献的发现不同，我们在实验中并未观察到自适应噪声 $\sigma$ 带来明显优势，因此将其作为固定超参数使用。

2.2. The impact of network parameterization

在 ES 中，探索是通过对策略参数 θ\thetaθ 做随机扰动来实现的。而像 Q-learning 和策略梯度那样的传统方法，一般是通过在动作层面进行随机采样来实现探索。对 ES 而言，若高斯扰动不够有效地改变策略的行为，就无法形成有效的性能差异，进而无从更新。在 Atari 游戏实验中，我们发现，对 DeepMind 提出的卷积网络结构直接加上随机参数扰动，往往不足以产生有效的探索：有些环境里，扰动导致的策略几乎只会一直采取同一动作，无法收集足够多的奖励。我们通过在策略中使用虚拟批归一化（virtual batch normalization），解决了大多数 Atari 游戏面临的这个问题。虚拟批归一化与批归一化（batch normalization）类似，区别在于其所用的“批”在训练开始时就固定不变。这样做在训练早期（当随机初始化的策略参数尚未充分拟合时），网络对输入图像的微小变化会更敏感，从而更容易在动作层面产生多样性。但对大多数场景而言，虚拟批归一化会增加一定的计算成本；然而在我们环境中，每回合需要的环境交互通常比一次前向运算要多很多步，因而这点额外开销基本可忽略。

3. Smoothing in parameter space versus smoothing in action space

如前所述，强化学习的主要困难之一在于目标函数梯度的缺失或难以获取：环境或策略可能是离散的、不光滑的，或者只能通过抽样获取高方差的估计。在最一般情况下，假设我们有一个决策问题，采取一序列动作 $a = \{a_1, ..., a_T\}$ ，得到回报 $R(a)$ ，其中 $a_t=\pi(s;\theta)$ 来自一个确定性或随机的策略。我们要优化的是

F(\theta)=R(a(\theta))

由于动作可以是离散的，策略也可以是确定性的， $F(\theta)$ 可能在 $\theta$ 上不光滑，更重要的是，环境的状态转移函数无法直接对我们开放，导致无法通过类似反向传播的方法来直接计算 $\theta$ 的梯度。

要让这个问题可微、且能找到其梯度的方式之一，就是在策略或参数中人工添加噪声。策略梯度方法 通常在动作空间加噪声，即令动作分布依赖于某种概率模型：例如在离散动作情形下，通过对策略打分做 softmax 来进行采样。这样做可得新的目标函数：

F_\text{PG}(\theta)=\mathbb{E}_\epsilon[R(a(\epsilon,\theta))]

和梯度估计：

\nabla_\theta F_\text{PG}(\theta)=\mathbb{E}_\epsilon[R(a(\epsilon,\theta)\nabla_\theta\log p(a(\epsilon,\theta);\theta)]

ES在参数空间加噪声，令 $\theta$ 扰动为 $\theta+\xi$ ，执行对应的动作 $a(\theta+\xi)$ ，可以也可以看作将 $F$ 做高斯平滑：

F_\text{ES}(\theta)=\mathbb{E}_\xi[R(a(\theta+\xi))]

和梯度估计：

\nabla_\theta F_\text{ES}=\mathbb{E}_\xi[R(a(\theta+\xi))\nabla_\theta \log p (\theta+\xi;\theta)]

3.1. When is ES better than policy gradients?

其方差大致可表示为：

\mathrm{Var}[\nabla_\theta F_{\mathrm{PG}}(\theta)] \;\approx\;\mathrm{Var}[R(a)]\,\mathrm{Var}[\nabla_\theta \log p(a;\theta)],\\\mathrm{Var}[\nabla_\theta F_{\mathrm{ES}}(\theta)] \;\approx\;\mathrm{Var}[R(a)]\,\mathrm{Var}[\nabla_\theta \log p(\tilde{\theta};\theta)].

若两种方法所做的探索程度相近， $\mathrm{Var}[R(a)]$ 差不多，区别在后面一项。对于Policy Gradients， $\nabla_\theta\log p(a;\theta)]=\sum^T_{t=1}\nabla_\theta\log p(a_t;\theta)$ ， $T$ 个不相关项之和，方差和 $T$ 近似线性增加；ES中 $\nabla_\theta\log p(\tilde{\theta};\theta)$ 和 $T$ 无关，因此ES适合在回合长度比较大的时候。而策略梯度为了对抗这个问题，通常会使用折扣奖励，或者利用价值函数逼近，以期降低高方差。但折扣奖励在长时序的情况下会带来偏差；价值函数逼近虽然有效，但也会引入相应的估计误差。相较而言，如果一个任务具有超长时序、延迟奖励且难以找到好的价值函数，则 ES 可能是更具吸引力的选择。

3.2. Problem dimensionality

从有限差分的方式解读ES。当 $\sigma$ 足够小的时候，考虑 $\theta'=\theta+\sigma\epsilon, \epsilon\sim\mathbb{N}(0,I)$ ，定义平滑后的目标 $J_\sigma(\theta)=\mathbb{E}_\epsilon[F(\theta+\sigma\epsilon)]$ ，有 $p_\theta(\theta')=\mathbb{N}(\theta';\sigma^2I)$ ，则

\begin{align*} \nabla_\theta J_\sigma(\theta)&=\nabla_\theta\int p_\theta(\theta')F(\theta')d\theta'\\ &=\int F(\theta')\nabla_\theta p_\theta(\theta')d\theta'\\ &=\int F(\theta')p_\theta(\theta')\nabla_\theta\log p_\theta(\theta')d\theta'\\ &=\mathbb{E}_\epsilon[F(\theta+\sigma\epsilon)\nabla_\theta\log p_\theta(\theta+\sigma\epsilon)] \end{align*}

且

\nabla_\theta\log p_\theta(\theta+\sigma\epsilon)=\frac{1}{\sigma^2}(\theta+\sigma\epsilon-\theta)=\frac{\epsilon}{\sigma}

（p是高斯分布）带回有：

\nabla_\theta J_\sigma(\theta)=\frac{1}{\sigma}\mathbb{E}_\epsilon[F(\theta+\sigma\epsilon)\epsilon]

把 $F(\theta+\sigma\epsilon)$ 做一阶泰勒展开有：

F(\theta+\sigma\epsilon)=F(\theta)+\sigma\nabla F(\theta)^{\top}\epsilon + O(\sigma^2)

带入前面的式子有：

\begin{align*}\mathbb{E}_\epsilon[F(\theta+\sigma\epsilon)\epsilon]&=\mathbb{E}_\epsilon[(F(\theta)+\sigma\nabla F(\theta)^{\top}\epsilon+O(\sigma^2))\epsilon]\\ &=\mathbb{E}_\epsilon[\epsilon F(\theta) + \sigma\nabla F(\theta)^{\top}\epsilon^2 + \epsilon O(\sigma^2)]\\ &=\sigma\mathbb{E}[\nabla F(\theta)^{\top}\epsilon^2]\\ &=\sigma\nabla F(\theta)\mathbb{E}[\epsilon\epsilon^{\top}]\\ &=\sigma\nabla F(\theta)I \end{align*}

然后除以 $\sigma$ 就是梯度+ $O(\sigma)$ ，总结有：

\nabla_\theta\eta(\theta)=\mathbb{E}_{\epsilon\sim\mathbb{N}(0,I)}[F(\theta+\sigma\epsilon)\frac{\epsilon}{\sigma}]=\mathbb{E}_{\epsilon\sim\mathbb{N}(0,I)}[(F(\theta+\sigma\epsilon)-F(\theta))\frac{\epsilon}{\sigma}]

就是对 $\partial F/\partial \theta$ 的随机有限差分估计。

有限差分在高维空间的复杂度随着维度增加，但是实际上这个维度是优化的难度，不是NN中的参数量。在实验中，我们发现，当网络结构更大时，ES 的表现往往更好。例如在 Atari 任务中，与 A3C 一样，我们也尝试了较小和较大两种卷积网络，发现较大网络反而在 ES 下收敛得更好。我们推测这与梯度优化大网络更容易找到平滑的局部极小点类似。

3.3. Advantages of not calculating gradients

除了并行效率以及对长时序任务的适应性外，类似 ES 这样的黑箱优化还具备以下优势：

通信开销低 ：分布式实现时仅需在节点间传递标量，而基于梯度的方法则需传递完整梯度。
对极端稀疏/延迟奖励的适应 ：ES 只需关注整条回合的总回报，不受奖励频度或时序的影响。
计算量更小 ：ES 无需反向传播和价值函数训练，大幅降低每回合的计算开销。
不存在梯度爆炸问题 ：相比可能出现梯度爆炸的传统方法，ES 通过参数扰动的平滑性避免了这类极端情况。此外，ES 更容易整合硬注意力（hard attention）等不可微模块。
适应低精度运算 ：在二值网络（binary neural networks）等低精度模型中，ES 不会出现梯度估计偏差问题。由于只需前向推理，ES 可在 TPU 等专注推理的硬件上运行。
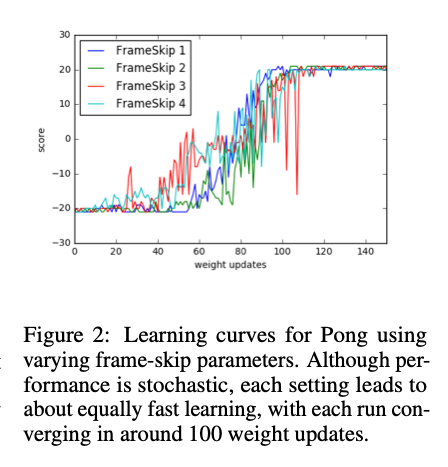
对动作频率不敏感 ：策略梯度需要精确调节 frame-skip——过高会损失细节控制能力，过低则引发长时序问题。而 ES 在参数空间引入噪声，策略在回合整体层面探索，无需考虑具体动作频率。这一特性使 ES 在需要分层（hierarchy）策略的任务中可能具有独特优势。

4. Experiments

4.1. MuJoCo

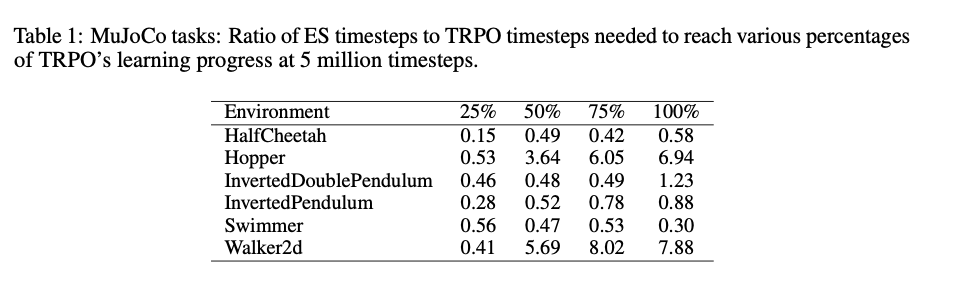
4.2. Atari

4.3. Parallelization

4.4. Invariance to temporal resolution

我们此处的主要贡献在于，展示了在现代分布式计算架构下，经过合理实现的 ES 在最难的一些 RL 环境上能够与主流方法同台竞技，并且在运行效率（Wallclock time）上可能更为有利。

6. Contribution

我们研究了一类黑箱优化算法——演化策略（ES），并将其作为 Q-learning、策略梯度等基于 MDP 的强化学习技术的一种替代选择。通过在 Atari 和 MuJoCo 上的实验，我们发现 ES 拥有一些有趣的优点：对动作频率和延迟奖励不敏感，不需要时间折扣或价值函数近似，而且高度可并行化。虽然其数据效率比一些最优的梯度方法略低，但能通过分布式并行来极大缩短训练时间。

展望未来，我们计划将 ES 应用于那些对于基于 MDP 的 RL 不太合适的场景：例如超长时序、复杂奖励结构的任务，或者需要元学习（meta-learning，learning-to-learn）等扩展。我们相信，在广阔的应用中，黑箱优化仍有许多价值有待挖掘，也希望更多研究能基于我们的结果进一步推动 ES 的发展与应用。

Evolution Strategies as a Scalable Alternative to Reinforcement Learning