摘要： Transformer模型在处理长序列时速度缓慢且消耗大量内存，因为自注意力（self-attention）的时间和内存复杂度与序列长度呈二次方关系。近似注意力方法试图通过权衡模型质量来减少计算复杂度来解决这个问题，但往往无法实现实际加速。我们认为，一个缺失的原则是让注意力算法对IO（输入/输出）敏感——考虑GPU内存各级之间的读写。我们提出了FlashAttention，一个考虑IO的精确注意力算法，通过使用切片技术减少GPU高带宽存储器（HBM）和GPU片上SRAM之间的内存读写次数。我们分析了FlashAttention的IO复杂度，显示它比标准注意力模型需要更少的HBM访问，并且对于一系列SRAM大小是最优的。我们还将FlashAttention扩展到块稀疏注意力，得到一个比任何现有近似注意力方法更快的近似注意力算法。FlashAttention比现有基准训练Transformer更快：与MLPerf 1.1训练速度记录相比，BERT-large（序列长度512）端到端实际加速15%，GPT-2（序列长度1K）加速3倍，以及在长距离竞技场（序列长度1K-4K）上加速2.4倍。FlashAttention和块稀疏FlashAttention使Transformer能够处理更长的上下文，产生更高质量的模型（在GPT-2上困惑度提高了0.7，在长文档分类上提高了6.4点）和全新的能力：这是首个在Path-X挑战（序列长度16K，61.4%准确率）和Path-256（序列长度64K，63.1%准确率）上实现超过机会水平性能的Transformer。

1. Intro

Attention：

Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V

中间一般会有Mask和Dropout。整个Attention的计算包括两次matmul，和各种element-wise的操作：mask，除法，softmax，dropout，这些操作访存次数非常多，计算整个Attention的过程总体来讲应当是memory bound的。

An important question is whether making attention faster and more memory-efficient can help Transformer models address their runtime and memory challenges for long sequences.

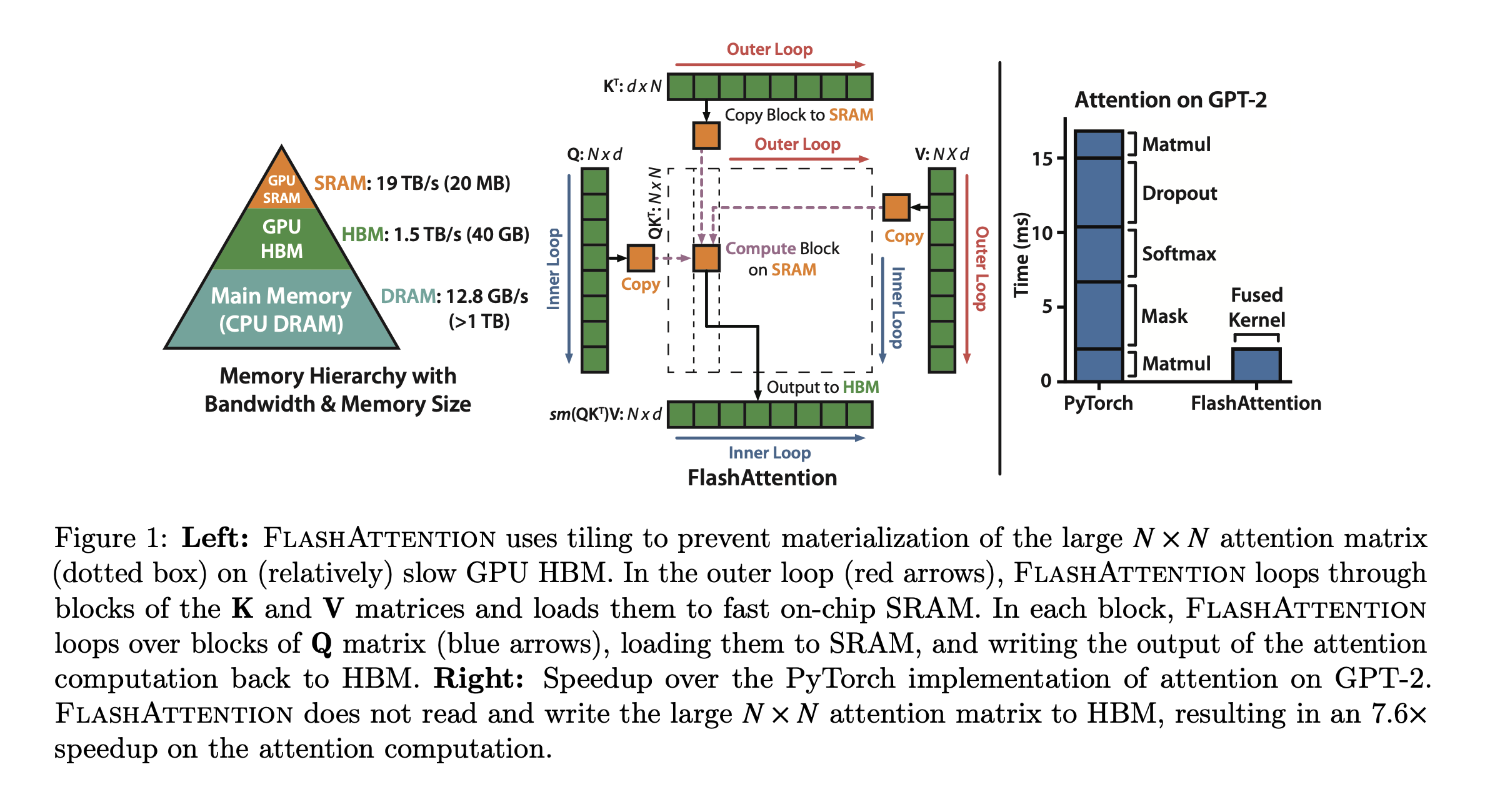
Attention是 $O(n^2)$ 的，之前的方法关注于如何用一个好的近似，在尽可能减少误差的情况下把计算Attention的操作变成线性或者近似线性的。但是这些方法只关注了”FLOW Reduction”，却没有考虑到IO的问题。

这篇文章首先指出在Transformer中无论是训练还是推理瓶颈都在于访存而不是计算，然后提出一种考虑IO的精确的Attention算法FlashAttention，它在各类任务上不仅训练更快并且能够产生更高质量的模型。

FlashAttention的主要目的是避免频繁从HBM（最慢）中读取数据，这就要求：

不需要完整的输入就能计算softmax；
在反向传播的过程中，不需要存储巨大的Attention矩阵。

FlashAttention的做法包括：

对QKV矩阵分块（tiling），在输入计算的时候可能会多次访问input block来执行softmax reduction；
在前向传播的时候，存储softmax归一化因子；这个方法和传统的把中间注意力矩阵存储到HBM，然后反向传播的时候读出来的方法快很多；
在CUDA级别写而不是python级别，更方便控制各种访存操作；做了算子融合；

FlashAttention方法实际上比标准的Attention方法有更高的FLOP，但是因为优化的好，计算的更快（比GPT-2快 $7.6\times$ ），内存占用也更少（和sequence length是线性的）。

We also show that FlashAttention can serve as a useful primitive for realizing the potential of approximate attention algorithms by overcoming their issues with memory access overhead.

为了证明解决访存瓶颈很重要，又提出一种新的block-sparse FlashAttention，通过对稀疏性的利用进一步提高了性能，不仅比FlashAttention快 $2.4\times$ ，而且还把sequence length拓展到了64k。

Contributions:

Faster Model Training . FlashAttention trains Transformer models faster in wall-clock time. We train BERT-large (seq. length 512) 15% faster than the training speed record in MLPerf 1.1, GPT2 (seq. length 1K) $3×$ faster than baseline implementations from HuggingFace and Megatron-LM, and long-range arena (seq. length 1K-4K) $2.4×$ faster than baselines.
Higher Quality Models. FlashAttention scales Transformers to longer sequences, which improves their quality and enables new capabilities. We observe a 0.7 improvement in perplexity on GPT-2 and 6.4 points of lift from modeling longer sequences on long-document classification. FlashAttention enables the first Transformer that can achieve better-than-chance performance on the Path-X challenge, solely from using a longer sequence length (16K). Block-sparse FlashAttention enables a Transformer to scale to even longer sequences (64K), resulting in the first model that can achieve better-than-chance performance on Path-256.
Benchmarking Attention . FlashAttention is up to $3×$ faster than the standard attention implementation across common sequence lengths from 128 to 2K and scales up to 64K. Up to sequence length of 512, FlashAttention is both faster and more memory-efficient than any existing attention method, whereas for sequence length beyond 1K, some approximate attention methods (e.g., Linformer) start to become faster. On the other hand, block-sparse FlashAttention is faster than all existing approximate attention methods that we know of.

2. Background

2.1. Hardware Performance

GPU Memory hierarchy ：如Fig1的左图，三级memory。非常多的thread（Kernel）从HBM中把数据加载到SRAM、寄存器中做计算。

Performance characteristics： 从roofline model的想法可以继续分成Compute-bound和Memory-bound。

Kernel Fusion： 算子融合，主要还是想避免多次从底层的memory中加载数据。编译器已经可以自己识别并且做elementwise操作的算子融合了。

2.2. Standard Attention Implementation

假设一个假设有一个multihead Attention参数分别是 $(N, d)$ ，则有三个矩阵 $Q, K, V \in \real^{N\times d}$ 。计算Self Attention的操作包括：

$S=QK^T\in \real^{N,N}$
$P=softmax(S)\in \real^{N,N}$
$O=PV\in \real^{N,d}$

$S$ 有的时候叫Attention Score， $P$ 叫Normalized Attention Scores或Attention weights， $O$ 是输出。

标准的方法涉及到很多次的HBM读写。

3. FlashAttention：Algorithm, Analysis, and Extensions

正文部分主要介绍前向传播，反向传播的过程放在Appendix中。

3.1. An Efficient Attention Algorithm with Tiling and Recomputation

Our goal is to reduce the amount of HBM accesses(to sub-quadratic in N).

Tiling

常用的稳定版softmax可以写作：

m(x):=\max_i x_i, f(x):=[e^{x_1-m(x)}, e^{x_2-m(x)}, ..., e^{x_n-m(x)}], l(x):=\sum_if(x)_i,\\ softmax(x):=\frac{f(x)}{l(x)}

对矩阵做softmax就是对其中的每一行分别做softmax。假设把 $x$ 向量分块为 $x=[x^{(1)}, x^{(2)}]$ ，则上面的式子可以写作：

m(x) = m\left[ x^{(1)}, x^{(2)} \right] = \max(m\left[ x^{(1)} \right], m\left[ x^{(2)} \right]),\\ f(x) = \left[ e^{m\left( x^{(1)} \right) - m(x)} f(x^{(1)}), e^{m\left( x^{(2)} \right) - m(x)} f\left( x^{(2)} \right) \right],\\ l(x) = l( x^{(1)}, x^{(2)}) = e^{m( x^{(1)}) - m(x)} l( x^{(1)}) + e^{m(x^{(2)}) - m(x)} l(x^{(2)}),\\ \text{softmax}(x) = \frac{f(x)}{l(x)}.

所以计算分块后的向量softmax的流程变为：

输入 $x^{(1)}$ , 计算 $m(x^{(1)}),f(x^{(1)})=[e^{x_1^{(1)}-m(x^{(1)})},....], l(x^{(1)})=\sum_if(x^{(1)})_i$
保存 $m = m(x^{(1)}), l = l(x^{(1)})$
$softmax(x^{(1)})=\frac{f(x^{(1)})}{l}$ ，这个数值是有问题的，因为 $m(x^{(1)})$ 和 $l$ 目前都不是全局的数值
输入 $x^{(2)}$ ，计算 $m(x^{(2)})$
更新 $m = max(m, m(x^{(2)}))$
计算 $f(x^{(2)})=[e^{x_i^{(2)}-m}, ...], l(x^{(2)})=\sum_if(x^{(2)})_i$
更新 $l =l+ l(x^{(2)})$
$softmax(x^{(2)})=\frac{f(x^{(2)})}{l}$ ，这个值就是正确的了
利用新保存的信息更新之前的有问题的值，即 $f^{new}(x^{(1)})=f(x^{(1)}*e^{m(x^{(1)})-m^{new}}, softmax^{new}(x^{(1)})=softmax(x^{(1)})*l(x^{(1)})*e^{m(x^{(1)})-m^{new}}/l$

要能够分块地计算softmax，就需要维护 $l(x^{(1)}), m(x^{(1)}), softmax(x^{(1)})$ 几个局部值和 $l, m$ 两个全局值，引入了 $O(n)$ 的额外计算（更新之前的值）和 $O(n)$ 的额外内存占用（存储局部值）。

Implementation details: Kernel Fusion

做kernel fusion减少把中间结果写回HBM再读取出来的操作。

现在考虑一个完整的Attention操作，再放一次上面的流程图：

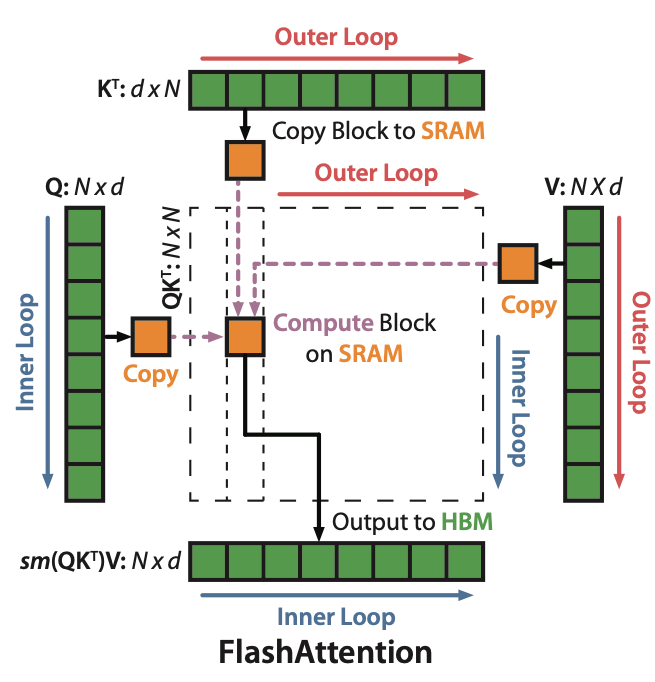
对QKV的分块都让它们变成(1,n)的分块向量，这样只要按照循环顺序计算块内-更新全局数据-更新旧数据，最终得到的数据和之前的Attention操作就是一样的。同时这种操作完全避免了显式地保存S和P两个矩阵，减少了写回。

Recomputation

传统的反向传播的方法都是存储中间结果S, P两个矩阵来计算Q,K,V的梯度。Flash Attention没有保存这两个矩阵，在进行反向传播的时候就要引入新的计算。

3.2. Analysis: IO Complexity of FlashAttention

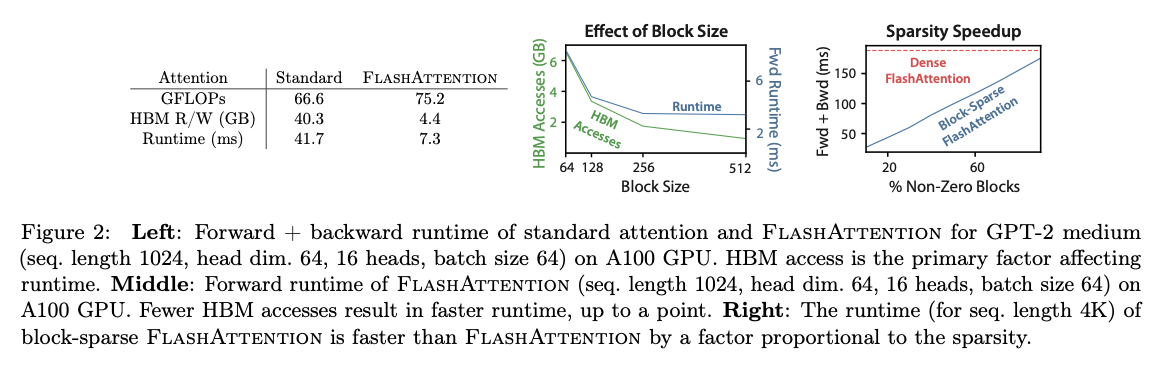
可以看到，FlashAttention的FLOP数反而升高了，因为中间涉及到了数据的重复计算（更新之前的softmax），但是HBM读写缩小到了几乎是之前的十分之一，导致运行时间缩短到了之前的约六分之一。

几个分析证明，假设 $seq\_length = N, M是SRAM的大小$ 并满足 $d\le M \le Nd$ ，则有：

标准Attention的算法要求至少 $\Theta(Nd+N^2)$ 次访存
FlashAttention要求至少 $\Theta(N^2d^2M^{-1})$ 次访存
计算Attention的下界是 $o(N^2d^2M^{-1})$

3.3. Extension: Block-Sparse FlashAttention

加了一个稀疏Mask，访存次数进一步下降，但是此时Attention退化为近似的Attention而不是准确的。

4. Experiments

Training Speed. Quality. Benchmarking Attention.

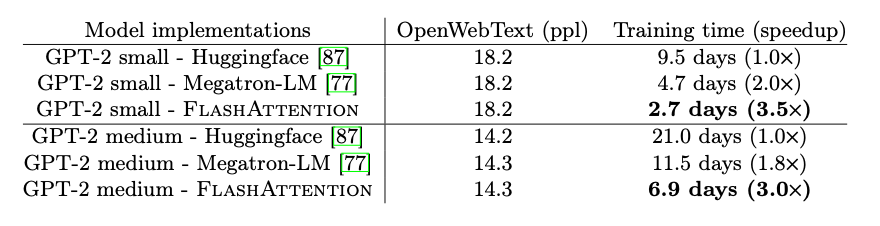
4.1. Faster Models with FlashAttention

BERT:

GPT-2：

Long-range Arena:

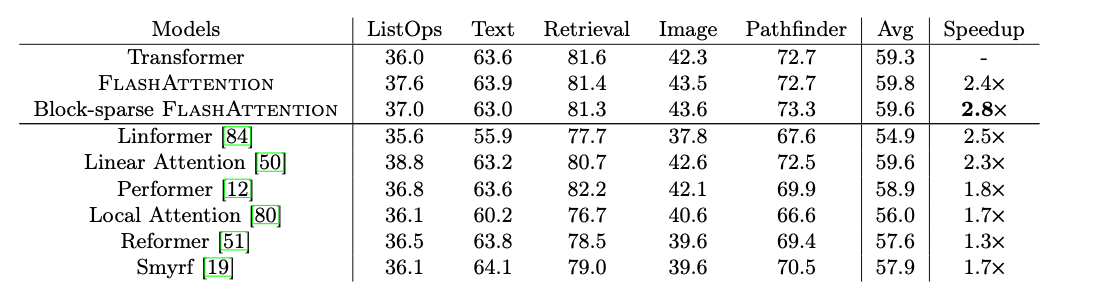
4.2. Better Models with Longer Sequences

Language Modeling with Long Context

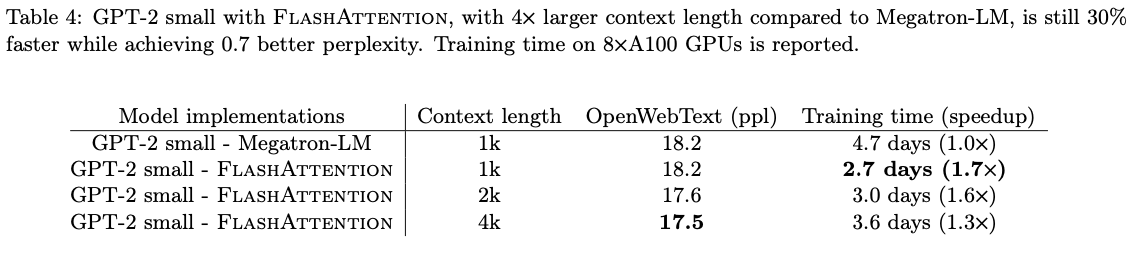
Long Document Classification

Path-X and Path-256

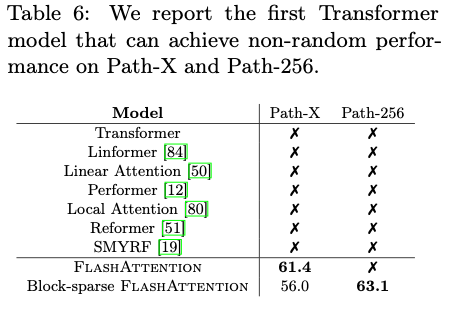
4.3. Benchmarking Attention

Runtime & Memory Usage

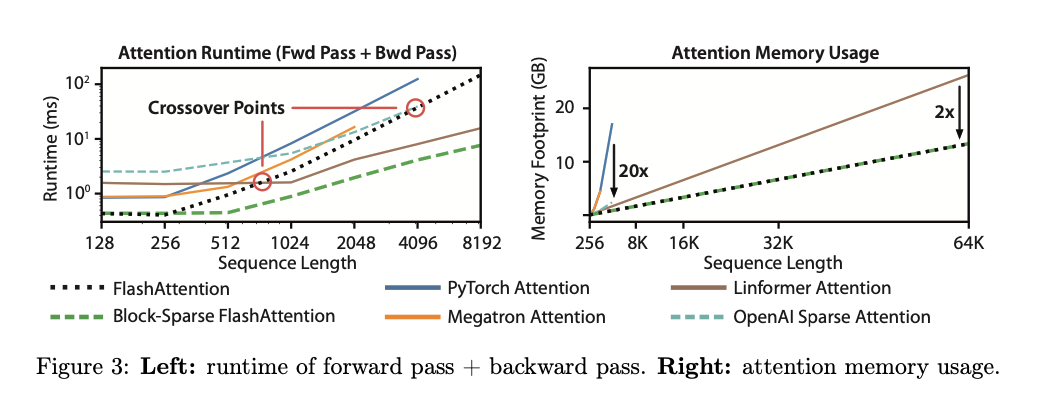
5. Limitation and Future Directions

Compiling To CUDA. These limitations suggest the need for a method that supports writing attention algorithms in a high-level language (e.g., PyTorch), and compiling to IO-aware implementations in CUDA—similar to efforts such as Halide in image processing.
IO-Aware Deep Leaning.
Multi-FPU IO-Aware Methods. Using multiple GPUs adds an additional layer to IO analysis—accounting for data transfer between GPUs. We hope our work inspires future work in this direction.

FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness