摘要： 模型大小和推理速度/功率已成为许多应用程序部署神经网络的主要挑战。解决这些问题的一个有前途的方法是量化。然而，将模型均匀量化为超低精度会导致显著的准确性退化。解决这个问题的一个新颖的解决方案是使用混合精度量化，因为与其他层相比，网络的某些部分可能允许较低的精度。然而，没有系统的方法来确定不同层的精度。蛮力方法对于深度网络是不可行的，因为混合精度的搜索空间在层数上是指数级的。另一个挑战是，在将模型量化为目标预切时，确定分组微调顺序的类似因子复杂性。在这里，我们介绍了Hessian AWare量化（HAWQ），这是一种新颖的二阶量化方法来解决这些问题。HAWQ允许根据该层的Hessian光谱自动选择每层的相对量化精度。此外，HAWQ为量化层提供了一个确定性的微调顺序。我们在使用ResNet20的Cifar-10上以及使用Inception-V3、ResNet50和SqueezeNext模型的ImageNet上展示了我们方法的结果。将HAWQ与最先进的技术进行比较表明，与最近提出的RVQuant和HAQ方法相比，我们可以在ResNet20上以8倍激活压缩率实现相似/更好的准确性，与最近提出的RVQuant和HAQ相比，ResNet50和Inception-V3上的精度更高1%，型号更小14%。此外，我们表明，我们可以将SqueezeNext量化为1MB模型大小，同时在ImageNet上实现68%以上的top1精度。

1. Intro

现在模型输入的规模比早期大了非常多，早期的MNIST数据只有 $1\times 28 \times 28$ ，而现在的ImageNet已经是这个规模的200倍有余了。而即使是ImageNet在自动驾驶等领域也被认为是过于小的输入了。输入规模的不断增大导致神经网络的训练与推理对算力的要求都水涨船高。

为了解决算力需求的问题，学界已经提出了若干种方法，包括

设计网络结构更简单、算力需求更小但能达到相同精度的网络
软硬联合设计，Co-designing
删除网络中多余的filter
使用量化方法
在量化的基础上结合AutoML方法对软硬件进行优化

这篇文章主要提出了一种新的量化方法。量化方法最大的问题是降低了模型精度之后准确率会显著下降。传统的量化方法将所有的层都量化到同一个精度，这显然是不对的，因为不同层需要的精度可能不同，量化太高模型太大，量化太低精度太低。

Contributions：

novel, deterministic method for determining the relative quantization level of layers based on the Hessian spectrum of each layer
a Hessian based method to determine fine-tuning order for different NN blocks
higher precision and smaller model size / activation size than sota

早期的模型如VGG-16，拥有非常庞大的全连接层。目前的设计趋向于减少使用这些FC层。
使用知识蒸馏的方法缩小模型
设计”both small and hardware-efficient”的模型，如SqueezeNet
量化

有一些层包含的信息确实很少，所以应该给出相当低的精度，但将所有的层都量化到那么低的精度是不可接受的；对于混合精度，通过搜索等方法的时间开销是不可接受的。本文的目标是通过利用一些“second order”信息。

3. Methodology

假设神经网络可以分成若干块 $\{B_1, B_2, ..., B_m\}$ ，每一块都有自己的参数 $\{W_1, W_2, ..., W_m\}$ 。一个块可能是一层或者多层（或者一个或者多个残差块）。则对于监督学习，损失函数：

L(\theta)=\frac{1}{N}\sum ^{N}_{i=1}l(x_i,y_i,\theta)

其中 $\theta\in \real^d$ 是 $\{W_1, W_2, ..., W_n\}$ 的组合， $l(x,y,\theta)$ 是数据 $(x,y)\in (X,Y)$ 的loss。训练结束后，通过

Q(z)=q_j, z\in(t_j, t_{j+1}]

将一般是32或64bit的整型权重量化到低阶的整数上。

但不同的层拥有不同的量化敏感度，而敏感度不同的层显然不能被量化到同一个级别上。

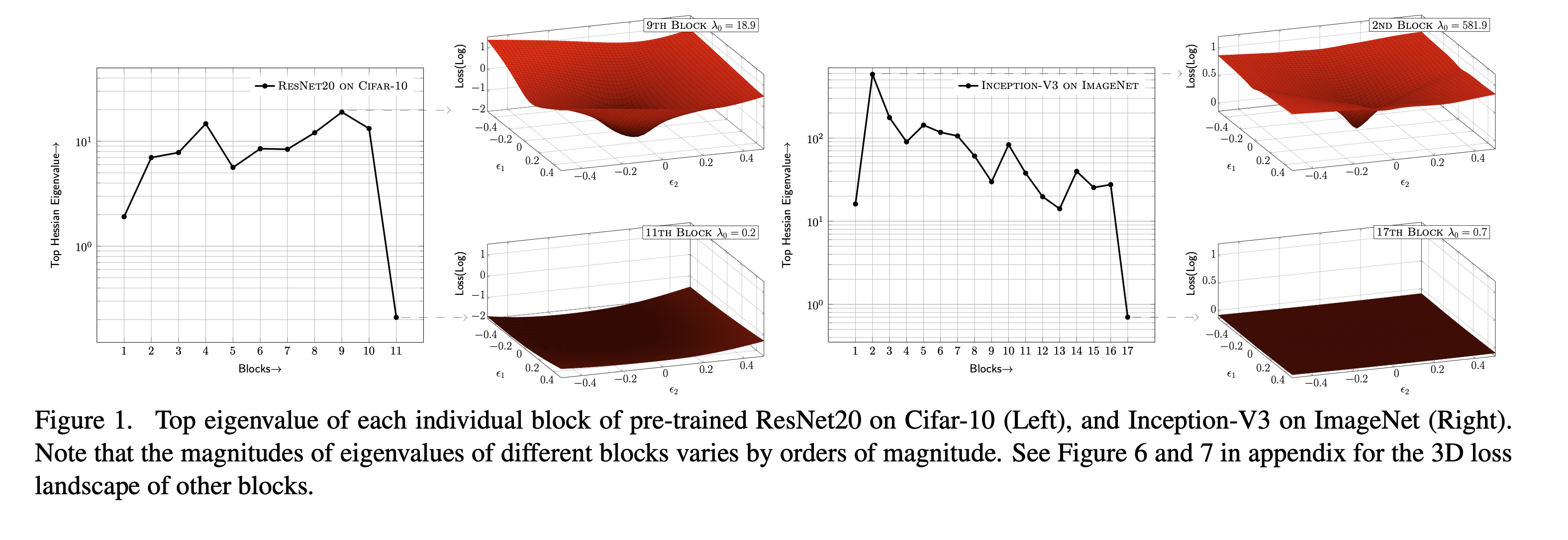
一种可能的用于分析量化敏感度的方法是使用“first order”的信息，即梯度向量。（这些first、second order一般指的是目标函数的一阶导或者二阶导）但是这种依赖一阶导数的方法可能会“very misleading”，比如二次函数 $y=\frac{1}{2}ax^2$ 在 $x=0$ 处一阶导和a无关。

来自GPT

在优化和机器学习中，“first-order”和”second-order”信息是用来描述目标函数（通常是损失函数）局部行为的术语。这些信息分别来自函数的一阶和二阶导数。

First-Order Information

First-order信息主要涉及到目标函数的梯度（或一阶导数）。在多维空间中，梯度是一个向量，其各个分量分别是目标函数相对于各个参数的偏导数。梯度向量指向函数值上升最快的方向。

在梯度下降等一阶优化算法中，梯度用于更新模型参数

Second-Order Information

Second-order信息涉及到目标函数的Hessian矩阵，这是一个二阶导数矩阵。Hessian矩阵描述了函数的曲率，即它如何在每个方向上弯曲。对于多维函数，Hessian矩阵包含所有二阶偏导数的组合。

在牛顿方法等二阶优化算法中，Hessian用于更精确地更新模型参数

为什么Second-Order信息可能更好？

Second-order信息（如Hessian矩阵）提供了关于目标函数局部行为的更多信息，包括其曲率。这样，优化算法可以更准确地确定应该如何更新参数。这通常可以导致更快的收敛和更好的优化结果。

然而，计算和存储Hessian矩阵通常都很昂贵，尤其是对于具有大量参数的模型。这就是为什么在实际应用中，二阶方法通常仅用于小到中等规模的问题。

在HAWQ中，通过使用Hessian矩阵进行敏感度分析，可以更精确地确定哪些层或参数可以被量化到较低的精度，从而在保持性能的同时，最大限度地减少计算和存储需求。

3.1 Second-Order Information

主要是分析了一下，实际不用计算完整的Hessian矩阵，说明Hessian矩阵的最大特征值大的说明频谱陡峭，说明量化敏感，说明需要的位宽更大，反之亦然。用幂迭代的方法可以计算出 $\lambda_i=||Hv||_2$ ，恰好又有关系

\frac{\partial (g_i^Tv)}{\partial W_i}=\frac{\partial g_i^T}{\partial W_i}v+g_i^T\frac{\partial v}{\partial W_i}=\frac{\partial g_i^T}{\partial W_i}v=H_iv

3.2 Algorithm

量化精度用 $S_i=\lambda_i/n_i$ 确定，引入参数数量和特征值两个条件。比较抽象的是每一层的bit-width居然是手动选择的

微调的顺序按照 $\Omega_i=\lambda_i||Q(W_i)-W_i||^2_2$ 确定，综合考虑特征值和量化误差。

4. Result

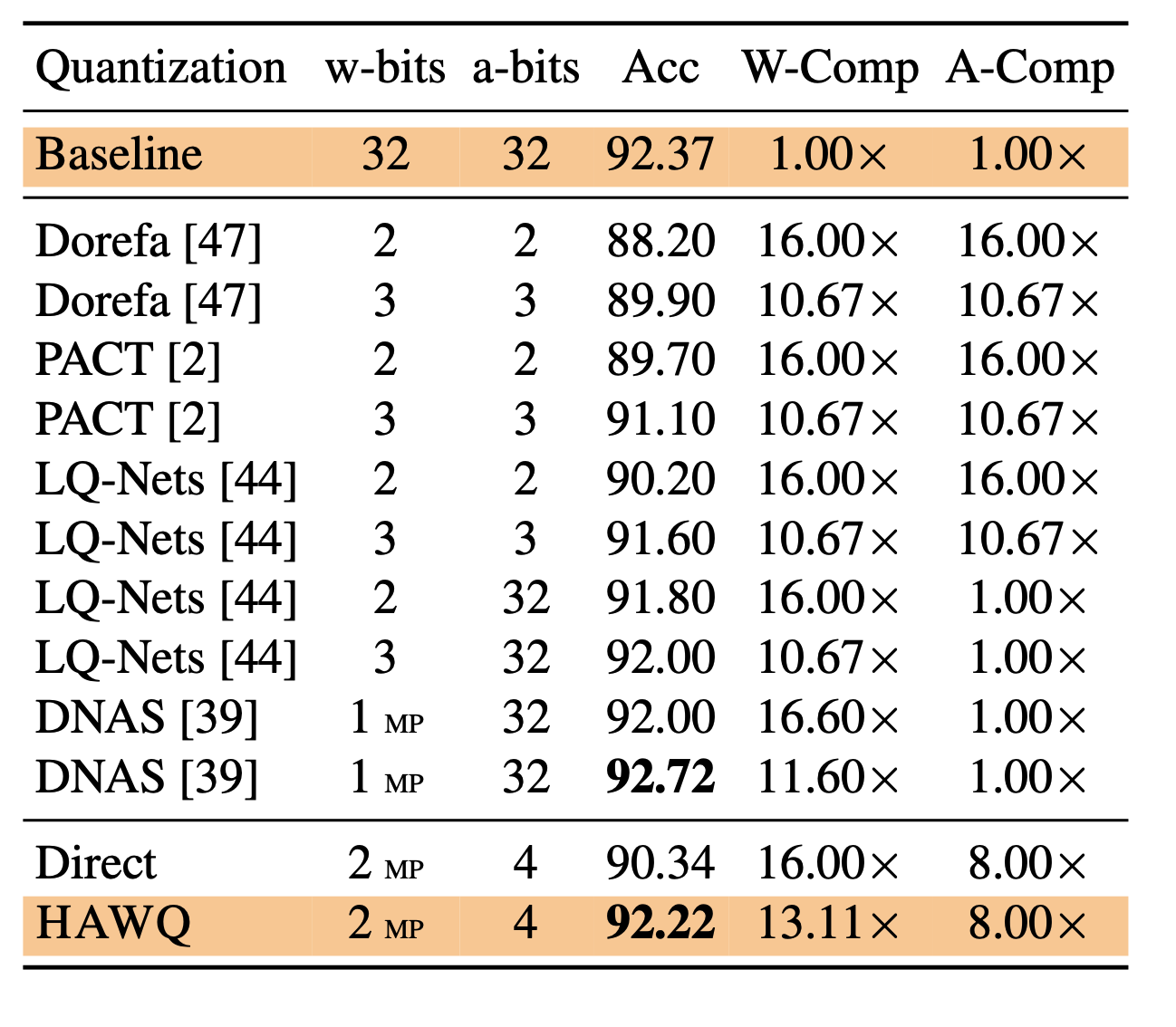
5. Ablation Study

混合精度量化的有效性

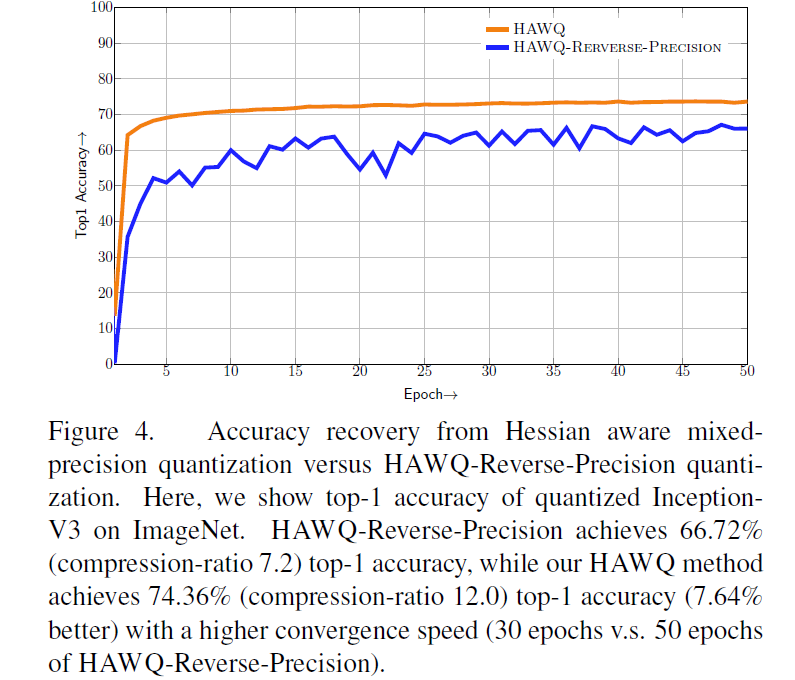
block-wise的有效性

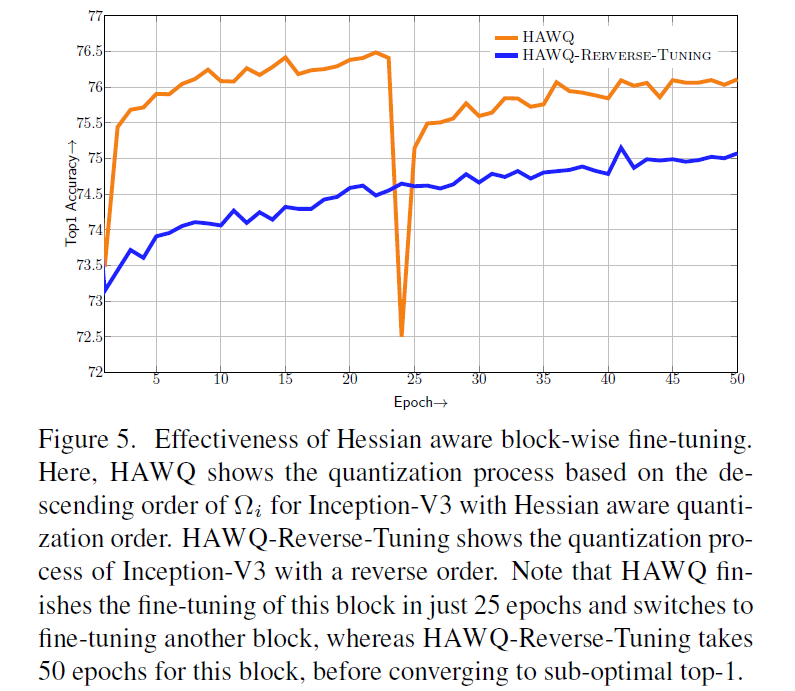
6. Conclusion

自己也提出来只确定了位宽的相对大小，不能确定实际值，之后需要改进。在HAWQ V2中就改进了。

HAWQ: Hessian Aware Quantization of Neural Networks with Mixed-Precision