摘要： 带线性注意力的 Transformer（即线性 Transformer）和状态空间模型（SSM）近来被认为是采用 softmax 注意力的 Transformer 的一种线性时间可行替代方案。然而，这些模型仍然不及标准 Transformer，尤其是在需要上下文内检索的任务上。尽管一种更具表达力的线性 Transformer 变体——用 Delta 规则替代线性 Transformer 中的加性更新（DeltaNet）——被发现对关联式回忆更有效，但用于训练此类模型的现有算法无法在序列长度维度并行，因此在现代硬件上训练效率低下。本文提出了一种硬件高效的算法，用于训练采用 Delta 规则的线性 Transformer。该算法利用一种用于计算 Householder 矩阵乘积的内存高效表示。借助该算法，我们得以将 DeltaNet 扩展到标准的语言建模设定。我们在 100B 词元上训练了一个 1.3B 参数模型，发现其在困惑度和下游任务零样本性能方面优于近期的线性时间基线模型，如 Mamba 和 GLA 。我们还尝试了两种混合模型：将 DeltaNet 层与（1）隔层插入的滑动窗口注意力层，或（2）两层全局注意力相结合，结果显示这些混合模型优于强力的 Transformer 基线。

1. Intro

Linear Attention的提出主要还是希望解决掉Transformer中二次复杂度的问题，KV Cache巨大显存占用的问题。通过将softmax注意力中的 $e^{x}$ 处理替换成直接的（或者其他经过变换的）点乘Kernel，可以将softmax注意力的KV Cache转换为一固定大小的Hidden State，实现常数内存大小需求的推理。

之前的如SSM，直接点乘方法的Linear Attention LLM在长序列召回任务上不如Transformer，但是近期的DeltaNet通过Delta规则检索并更新，在长序列召回任务上有比较大的潜力。但是，由于DeltaNet的写法是完全顺序的，无法跨序列长度并行，导致难以scale up，硬件利用率低。

2. Background

2.1. Linear Transformer: Transformers with Linear Attention

给定一个 $d$ 维的输入 $[x_{1}, ..., x_{L}]$ ，Transformer的注意力：

q_{t}, k_{t}, v_{t} = W_{Q} x_{t}, W_{K} x_{t}, W_{V} x_{t}, o_{t} = i = 1 \sum t \frac{exp ( k _{i}^{⊤} q _{t} )}{\sum _{i = 1}^{t} exp ( k _{j}^{⊤} q _{t} )} v_{i}

Linear Attention将 $exp (k_{i}^{⊤} q_{t})$ 替换为 $ϕ (k_{t})^{⊤} ϕ (q_{t})$ ， $ϕ : R^{d} \to R^{n}$ 的一个核函数。这意味着计算可以重新排序为：

o_{t} = i = 1 \sum t \frac{ϕ ( k _{i} ) ^{⊤} ϕ ( q _{t} )}{\sum _{i} = 1 ^{t} ϕ ( k _{j}^{⊤} ) ϕ ( q _{t} )} v_{i} = \frac{( \sum _{i = 1}^{t} v _{i} ϕ ( k _{i} ) ^{⊤} ) ϕ ( q _{t} )}{( \sum _{j = 1}^{t} ϕ ( k _{j} ) ^{⊤} ) ϕ ( q _{t} )} = \frac{S _{t} ϕ ( q _{t} )}{z _{t}^{⊤} ϕ ( q _{t} )},

其中 $S_{t} = \sum_{i = 1}^{t} v_{i} ϕ (k_{i})^{⊤} \in R^{d \times n}, z_{t} = \sum_{i = 1}^{t} ϕ (k_{i}) \in R^{n}$ .

当 $n \to \infty$ 时，Linear Attn选用多项式相关的 $ϕ (\cdot)$ 理论上可以从任意精度逼近softmax注意力。一些工作发现 $z_{t}^{⊤} ϕ (q_{t}) \in R$ 存在数值不稳定的情形，因此将它去除。一种简化的Linear Transformer：

S_{t} = S_{t - 1} + v_{t} k_{t}^{⊤}, o_{t} = S_{t} q_{t}

Efficient training

为了实现上面的高效训练，假设 $Q, K, V \in R^{L \times d}$ 是堆叠后的 $q, k, v$ ，则可以并行计算 $O \in R^{L \times d}$ ：

O = (Q K^{T} ⊙ M_{L}) V

$M_{L} \in R^{L \times L}$ 是因果mask。这个模式和前面的递归模式各有取舍：并行模式需要 $O (L^{2} d + L d^{2})$ 的FLOPs（多算了一个 $Q K^{⊤}$ ，实际上递推的时候只要算 $L$ 次 $d^{2}$ 的隐状态更新），但是可以把GPU吃满；递归模式只需要 $O (L d^{2})$ ，但是无法跨序列长度进行并行，难以利用Tensor Core进行加速。

Chunkwise parallel form

为了在上面两个状态中进行权衡，可以进行分块并行。将 $Q, K, V$ 按照长度 $C$ 切分为 $L_{C}$ 个chunk。记第 $t$ 个块中 $Q [t] \in R^{C \times d}$ ，状态可以重新标记为： $S_{i} [t] = S_{tC + 1}$ ，并定义 $S_{0} [t] = S_{C} [t - 1]$ ，即初始状态是上一个块的末状态，则：

S_{r} [t] = S_{0} [t] + i = 1 \sum t v_{i} [t] k_{i}^{⊤} [t], o_{r} [t] = S_{0} [t] q_{r} [t] + i = 1 \sum r v_{i} [t] (k_{i}^{⊤} [t] q_{r} [t])

记 $S [t] = S_{0} [t]$ ，块内改写为并行形式：

S [t + 1] = S [t] + V^{⊤} [t] K [t] \in R^{d \times d}, O [t] = Q [t] S^{⊤} [t] + (Q [t] K^{⊤} [t] ⊙ M_{C}) V [t]

这样跨块之间传递的只包括 $S [t]$ ，中间状态 $S_{i} [t]$ 不用落盘，复杂度变为 $O (L C d + L d^{2})$ 做 $O (L / C)$ 步。

2.2. DeltaNet: Linear Transformers with the Delta Update Rule

注意到上面的Linear Transformer采用线性递推：

S_{t} = S_{t - 1} + v_{t} k_{t}^{⊤}

纯加性地将新的 $k - v$ 对写入记忆中。但是这种记忆模式难以“回收”过去的关联，在 $L > d$ 的时候容易出现key collision的现象。理想的模型应该能够移除掉不重要的关联，为新的信息腾出空间。

DeltaNet的Delta Rule：

S_{t} = S_{t - 1} - β_{t} (S_{t - 1} k_{t} - v_{t}) k_{t}^{⊤}

其中 $β$ 是学习绿， $S_{t - 1} k_{t}$ 是当前预测， $v_{t}$ 是目标value。核心是根据预测与目标之间的delta来更新权重，这一过程还可以视为对online regression loss做单步SGD优化：

L_{t} (S) = \frac{1}{2} ∣∣ S k_{t} - v_{t} ∣ ∣^{2}, S_{t} = S_{t - 1} - β_{t} \nabla_{S_{t - 1}} L_{t} (S_{t - 1}) = S_{t - 1} - β_{t} (S_{t - 1} k_{t} - v_{t}) k_{t}^{⊤}

相对的，普通的Linear Attention（上面的加性版本）则是online linear (negative inner-product) loss $L_{t} = - ⟨ S k_{t}, v_{t} ⟩^{3}$ 进行优化。

从KV检索的角度来理解，可以看成先用当前的key获得旧的value：

v_{t}^{old} = S_{t - 1} k_{t}

然后将新旧一起进行差值：

v_{t}^{new} = β_{t} v_{t} + (1 - β_{t}) v_{t}^{old}

然后根据这个移除旧的、写入新的：

S_{t} = S_{t - 1} - v_{t}^{old} k_{t}^{⊤} + v_{t}^{new} k_{t}^{⊤}

Schlag 等人证明，在小规模 语言建模与合成的上下文检索任务上，DeltaNet 优于普通线性 Transformer。然而，他们基于线性 Transformer 内存高效递归实现 的训练算法是严格顺序 的，正如(下文3.2)所指出的那样，对现代硬件并不友好。这促使我们在下文给出一个等价的分块算法 ，以便在更大规模上训练 DeltaNet。

3. Paralelizingn DeltaNet Across the Sequence Dimension

3.1. A Memory-efficient Reparameterization

首先注意到， $S_{t}$ 也是可以写成加性的形式的：

S_{t} = i = 1 \sum t u_{i} k_{i}^{⊤}, u_{i} = v_{i}^{new} - v_{i}^{old} = β_{i} (v_{i} - v_{i}^{old})

因此如果我们能够构造出所有的 $u_{i}$ ，就能够

O = (Q K^{⊤} ⊙ M) U, U = stack_{row} (u_{1}, \dots, u_{L})

但是，如果我们朴素地计算 $u_{t}$ ，需要计算每一个 $S_{t - 1}$ 来得到 $v_{t}^{old}$ ，需要 $O (d^{2})$ 的内存。下面通过归纳法，利用Householder矩阵乘积证明，实际上我们只需要 $O (d)$ 的内存。

显然有：

S_{1} = β_{1} v_{1} k_{1}^{⊤} ⟹ u_{1} = β_{1} v_{1}

从DeltaNet本身出发：

S_{t} = S_{t - 1} - v_{t}^{old} k_{t}^{⊤} + v_{t}^{new} k_{t}^{⊤} = S_{t - 1} - β_{t} (S_{t - 1} k_{t}) k_{t}^{⊤} + β_{t} v_{t} k_{t}^{⊤} = S_{t - 1} (I - β k_{t} k_{t}^{⊤}) + β v_{t} k_{t}^{⊤}

注意到 $I - β k_{t} k_{t}^{⊤}$ 是一广义Householder变换。 $\prod_{j} (I - β_{j} k_{j} k_{j}^{⊤})$ 可以写作 $W - Y$ 表示： $P_{r} = I - \sum_{i = 1}^{r} w_{i} k_{i}^{⊤}$ ，其中 $w_{i}$ 由前面的 ${w_{< i}, k_{< i}}$ 和当前的 $(β_{i}, k_{i})$ 生成。

归纳展开得到：

S_{t} = i = 1 \sum t - 1 u_{i} k_{i}^{⊤} + β_{t} (v_{t} - i = 1 \sum t - 1 u_{i} (k_{i}^{⊤} k_{t})) k_{t}^{⊤}

从而：

u_{t} ≜ β_{t} (v_{t} - i = 1 \sum t - 1 u_{i} (k_{i}^{⊤} k_{t})), S_{t} = i = 1 \sum t u_{i} k_{i}^{⊤}

得到了不需要构造 $S_{t - 1}$ 也可以求得的 $u_{t}$ ，只需要 $O (d)$ 内存。具体而言，

S_{n} = S_{n - 1} (I - β_{n} k_{n} k_{n}^{⊤}) + β_{n} v_{n} k_{n}^{⊤} = (t = 1 \sum n - 1 u_{t} k_{t}^{⊤}) (I - β_{n} k_{n} k_{n}^{⊤}) + β_{n} v_{n} k_{n}^{⊤} = t = 1 \sum n - 1 u_{t} k_{t}^{⊤} - (t = 1 \sum n - 1 u_{t} k_{t}^{⊤}) β_{n} k_{n} k_{n}^{⊤} + β_{n} v_{n} k_{n}^{⊤} = t = 1 \sum n - 1 u_{t} k_{t}^{⊤} + u_{n} (β_{n} v_{n} - β_{n} t = 1 \sum n - 1 u_{t} (k_{t}^{⊤} k_{n})) k_{n}^{⊤} = t = 1 \sum n u_{t} k_{n}^{⊤}

然而，直接计算所有 $u_{t}$ 需要 $O (L^{2} d)$ 并且无法并行，因此还需要：

3.2. Chunkwise Parallel Form for DeltaNet

首先将递推式展开：

S_{t} = S_{t - 1} (I - β_{t} k_{t} k_{t}^{⊤}) + β_{t} v_{t} k_{t}^{⊤} = i = 1 \sum t β_{i} (v_{i} k_{i}^{⊤}) (j = i + 1 \prod t (I - β_{j} k_{j} k_{j}^{⊤}))

定义：

P_{i}^{j} = t = i \prod j (I - β_{t} k_{t} k_{t}^{⊤}), H_{i}^{j} = t = i \prod j β_{t} (v_{t} k_{t}^{⊤}) P_{t + 1}^{j}

广义Householder，化简：

P_{n} = t = 1 \prod n (I - β_{t} k_{t} k_{t}^{⊤}) = P_{n - 1} (I - β_{n} k_{n} k_{n}^{⊤}) = (I - t = 1 \sum n - 1 w_{t} k_{t}^{⊤}) (I - β_{n} k_{n} k_{n}^{⊤}) = I - t = 1 \sum n - 1 w_{t} k_{t}^{⊤} - β_{n} k_{n} k_{n}^{⊤} + (t = 1 \sum n - 1 w_{t} k_{t}^{⊤}) β_{n} k_{n} k_{n}^{⊤} = I - t = 1 \sum n - 1 w_{t} k_{t}^{⊤} - w_{n} (β_{n} k_{n} - β_{n} t = 1 \sum n - 1 (w_{t} (k_{t}^{⊤} k_{n}))) k_{n}^{⊤} = I - t = 1 \sum n w_{t} k_{t}^{⊤}

分块：

S_{i} [t] = S_{tC + i}, P_{r} [t] = P_{tC + 1}^{tC + r}, H_{r} [t] = H_{tC + 1}^{tC + r}

块内递推：

S_{r} [t] = S_{0} [t], P_{r} [t] + H_{r} [t]

与3.1中类似地，

P_{r} [t] = I - i = 1 \sum r w_{i} [t] k_{i} [t]^{⊤}, H_{r} [t] = i = 1 \sum r u_{i} [t] k_{i} [t]^{⊤}

且 $w_{r} [t], u_{r} [t] \in R^{d}$ 的递推：

w_{r} [t] = β_{r} [t] (k_{r} [t] - i = 1 \sum r - 1 w_{i} [t] (k_{i} [t]^{⊤} k_{r} [t])), u_{r} [t] = β_{r} [t] (v_{r} [t] - i = 1 \sum r - 1 u_{i} [t] (k_{i} [t]^{⊤} k_{r} [t]))

故：

S_{r} [t] = S_{0} [t] - S_{0} [t] (i = 1 \sum r w_{i} [t] k_{i} [t]^{⊤}) + i = 1 \sum r u_{i} [t] k_{i} [t]^{⊤} = S_{0} [t] + i = 1 \sum r (u_{i} [t] - S_{0} [t] w_{i} [t]) k_{i} [t]^{⊤} o_{r} [t] = S_{r} [t] q_{r} [t] = S_{0} [t] q_{r} [t] + i = 1 \sum r (u_{i} [t] - S_{0} [t] w_{i} [t]) (k_{i} [t]^{⊤} q_{i} [t])

同样地，将 $S [t] = S_{0} [t]$ ，有：

S [t + 1] = S [t] + (U [t] - W [t] S [t]^{⊤})^{⊤} K [t] O [t] = Q [t] S [t]^{⊤} + (Q [t] K [t]^{⊤} ⊙ M) (U [t] - W [t] S [t]^{⊤})

Practical considerations

考虑到块内的 $o_{r} [t]$ 的写法仍然是递推的，难以高效利用Tensor Core。引入UT变换¹：

T [t] = (I + tril (diag (β [t]) K [t] K [t]^{⊤}, - 1))^{- 1} diag (β [t]) W [t] = T [t] K [t], U [t] = T [t] V [t]

从而将大多数运算改写为matmul，使得状态更新得到了几乎与一般Linear Attention一样的计算流程。在BP中，通过重计算Hidden State节省显存。

Speed comparison

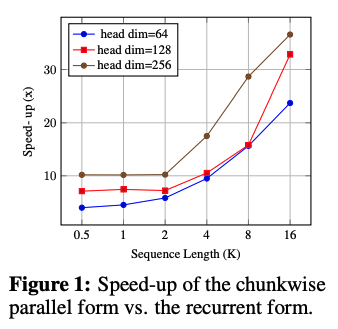
基于Triton实现了纯递归和Chunkwise两种，Chunckwise由于可以更好地利用Tensor Core往往能有很多倍的提升。

Fully Parallel Form for DeltaNet

注意力矩阵：

A_{ij} = {k_{j}^{⊤} P_{j + 1}^{i} q_{i}, 0, j \leq i, j > i,

同样可以写成 $A = (Q K^{⊤} ⊙ M) T$ 的形式，但是计算 $T$ 需要对上面的UT变换得到的内容求逆，如果写成完全并行的模式复杂度变成三次方，因此在训练中不采用完全并行形式；但该“注意力”矩阵对 RNN 可解释性研究可能有用。

3.3. DeltaNet Transformer

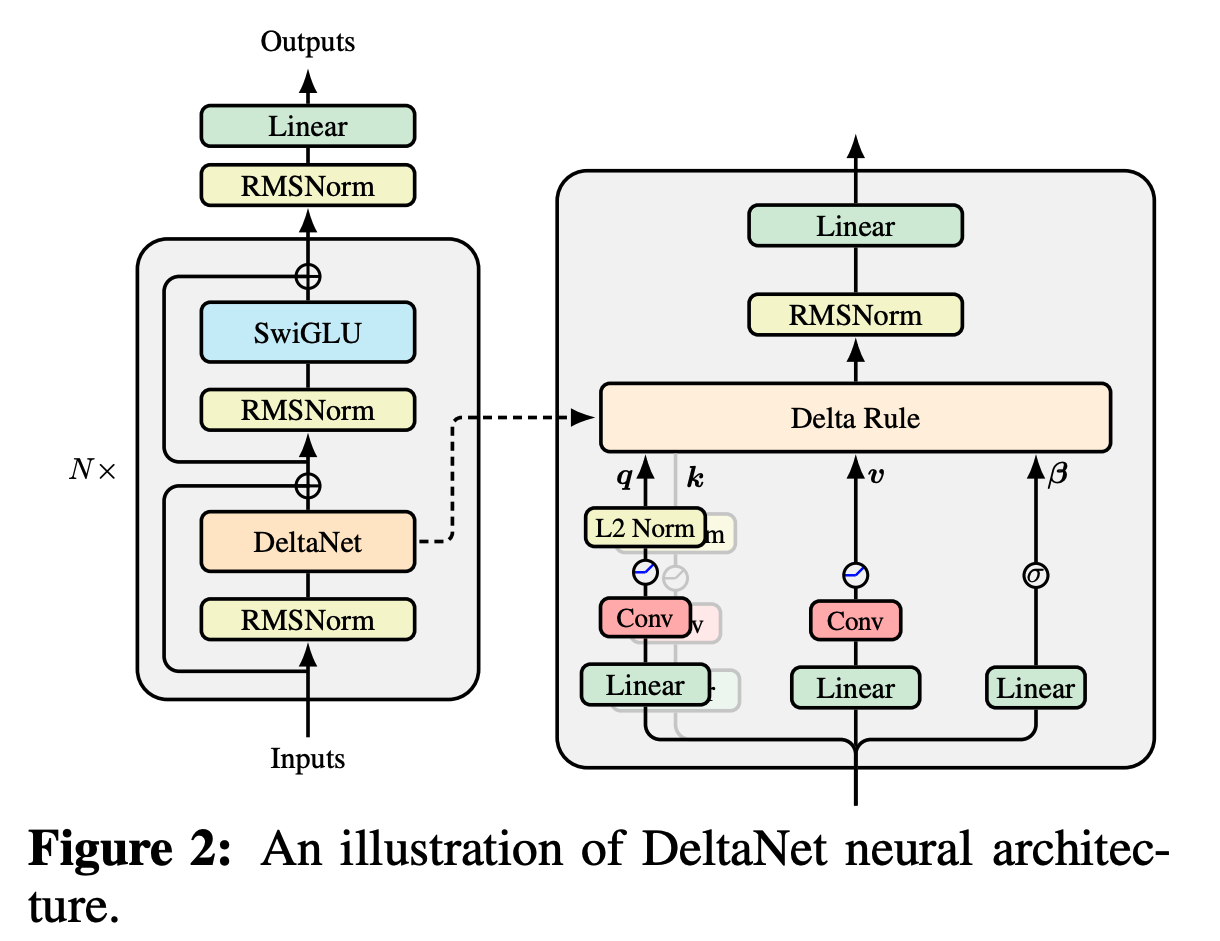
结构类似LLaMA/Transformer++，将自注意力的地方换成上面的DeltaNet，输入前添加RMSNorm增强训练稳定性。参数和Transformer++类似，DeltaNet层约 $4 d^{2}$ ，SwiGLU层约 $8 d^{2}$ 。

Feature map and normalization

将key & query定义为：

k_{t} = \frac{SiLU ( W _{K} x _{t} )}{∥ SiLU ( W _{K} x _{t} ) ∥ _{2}}, q_{t} = \frac{SiLU ( W _{Q} x _{t} )}{∥ SiLU ( W _{Q} x _{t} ) ∥ _{2}}

为了稳定，需要保证状态转移矩阵的特征值模长不超过1。对于：

I - β_{t} k_{t} k_{t}^{⊤}

有 $d - 1$ 个特征值为 $1$ ， $1$ 个为 $1 - β_{t} ∣∣ k_{t} ∣ ∣_{2}^{2}$ 。本文采用L2归一化：当 $β_{t} = 1$ 的时候 $I - k_{t} k_{t}^{⊤}$ 变成投影矩阵，在一个子空间中“抹除”信息，同时保留其他 $d - 1$ 个子空间的信息。

3.4. Hybrid Models

Convolutional layers

在 $Q / K / V$ 矩阵投影之后接一个比较小的Depthwise separable卷积，本文采用。

Local sliding window and global attention

Linear Attention比较依赖于“content-based addressing”，缺乏”positional information”，因此在强检索（retrieval-intensive）任务上受限。因此：

Sliding window attention(SWA)，和DeltaNet层交替堆叠；
Global Attention，将第2层和第 $(N /2 + 1)$ 层替换为global attn。

4. Empirical Study

4.1. Synthetic Benchmark

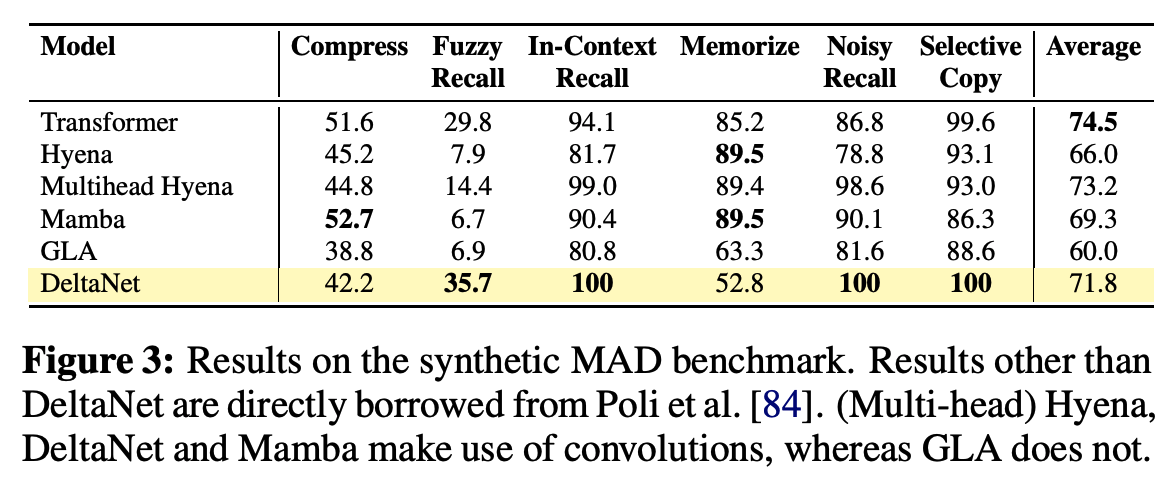
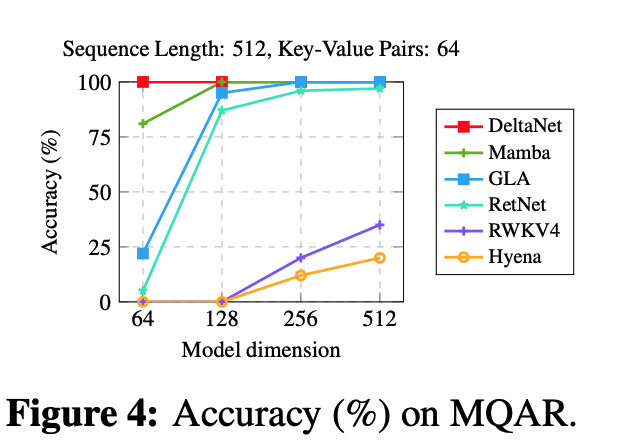
4.2. Language Modeling

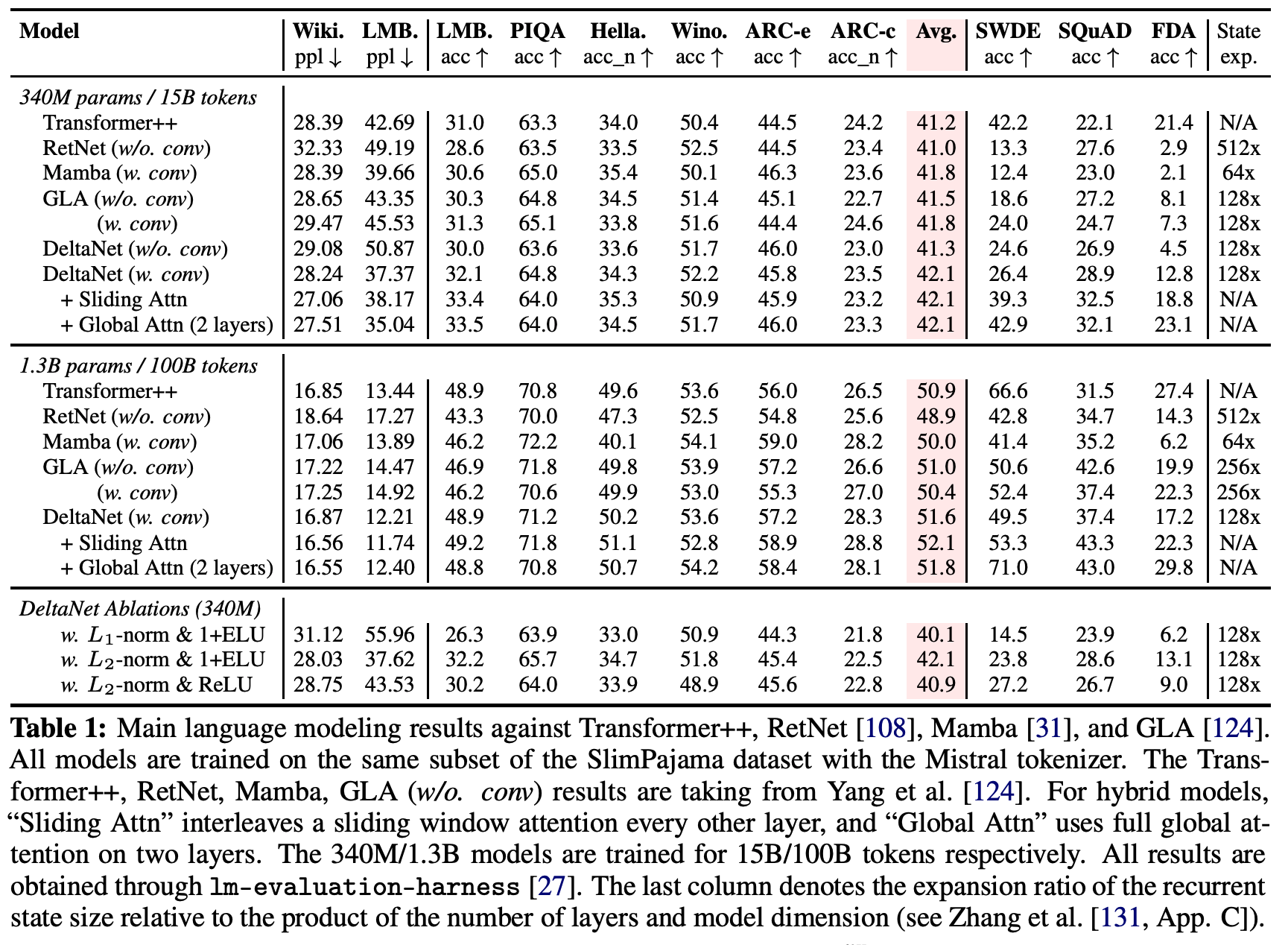
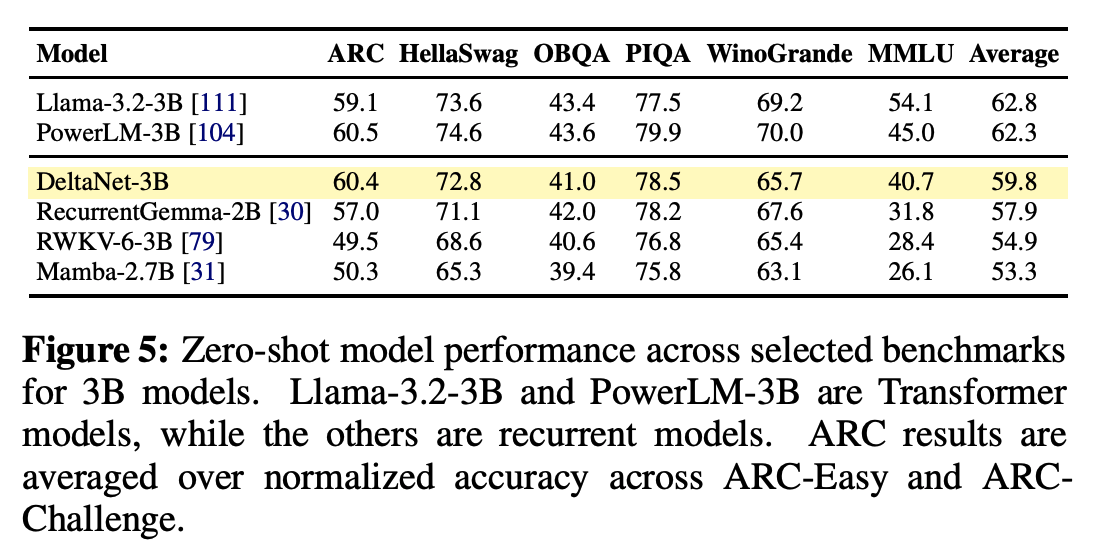
Ablations

主要是L1 Norm vs. L2 Norm, ReLU vs. 1+ELU

Training throughput

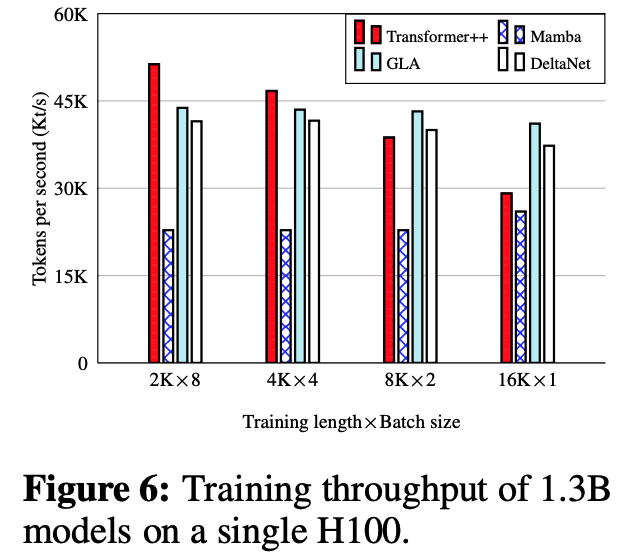
长序列上能超过Transformer++，短序列应该是因为Tensor Core用不满？Training确实是Compute Bound。

5.1. DeltaNet vs. State Space Models/Linear RNNs

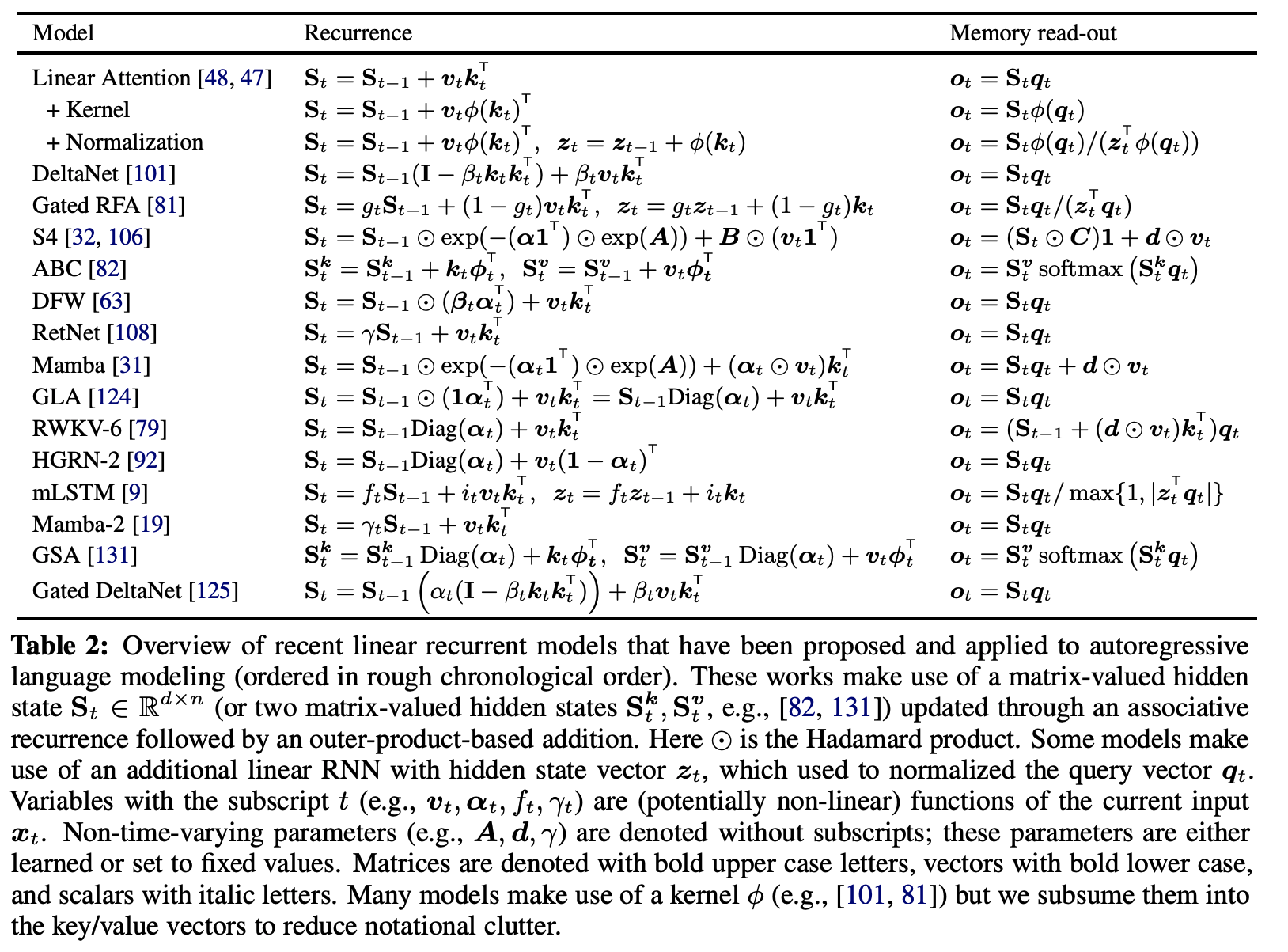
考虑一类“具有Hidden State Matrix、assiciative“的RNN，可以写作；

S_{t} = S_{t - 1} \cdot M_{t} + v_{t} k_{t}^{⊤} (recurrence) o_{t} = S_{t} q_{t} （ memory read-out ）

其中 $\cdot$ 是一个可结合的算子（矩阵乘，Hadamard乘法，…）。

这种RNN可以通过并行扫描的方法，以 $O (lo g L)$ 步， $O (L)$ 工作量计算 $[S_{1}, ..., S_{L}]$ 。因此，只要 $\cdot$ 本身的开销不打，训练就会是高效的。然而，很多 $\cdot$ 就是有很大的计算量，最近的工作如Mamba, Gated Linear Attention Transformer就用 $⊙$ 逐元素乘法作为 $\cdot$ 。

另一方面，matmul的表达能力当然比 $⊙$ 强，但是如果对 $M_{t}$ 不施加任何限制/结构先验，每步的更新量从之前的 $O (d n)$ 变成 $O (d n^{2})$ ，代价过高。DeltaNet采用

M_{t} = I - β_{t} k_{t} k_{t}^{⊤}

相当于引入了结构化的先验，是上面两者的一个折中。

本文提出的Chunkwise算法还可以推广到更加一般的“对角加低秩“（Diagnoal-Plus-Low-Rank）形式：

M_{t} = D - a_{t} b_{t}^{⊤}

S4中讨论过这个形式，但它的做法让 $M_{t}$ 不是input dependent的²。本工作则需要input dependent。

5.2. Towards a Unifying Framework for Efficient Autoregressive Sequence Transformations

尽管上述类模型有助于统一近期方法，我们并不声称它就是观察自回归序列变换的“唯一正确层次 ”。

序列变换形如：

{x_{t}}_{t = 1}^{L} \to {o_{t}}_{t = 1}^{L}

且 $o_{t}$ 不得依赖于 $x_{j}, j > t$ （就是因果）。

例如，这一框架不易整齐地涵盖其他已被证明有效的次二次 方法。另一种统一思路是把上述序列变换看作连续状态空间模型 的离散化，或视作与掩码结构矩阵 相乘。更关键的是，一个好的框架应当能催生高效的训练算法 ，并且对硬件友好 ——在现代 GPU 上，这通常意味着富含矩阵乘 。

5.3. Limitations and Future Work

本工作仍有若干局限。首先在计算方面，尽管我们提出了新的硬件高效算法，其训练速度仍落后于 GLA。这是因为我们在内核中对状态间依赖 的建模引入了开销，需要在 head 维度上做“边缘化 ”，这与 softmax 注意力 的情形类似；而对 GLA 而言，不存在** 状态内依赖**（全为逐元素），因此易于通过** Tiling支持任意 head 维度。这一限制可能会限制 DeltaNet 的状态容量**，从而降低强召回任务的表现（与 §4.2 的观察一致）。一种潜在改进是采用** 块对角的广义 Householder 过渡矩阵，使块大小适配 GPU SRAM（如 128），在保持 整体较大 head 维度**（即较大循环状态）的同时降低内核负担。其次，我们发现 DeltaNet 的长度泛化 有限；相对地，GLA 与 RetNet（以及一定程度上的 Mamba）在外推长于训练序列 方面更好。我们推测这是因为 DeltaNet 缺少显式衰减因子 。可考虑在递推中引入门控项 进行改进。

线性 Transformer 可被视为一种迭代 Hopfield 网络 ；这一联系有助于理解线性注意力的局限与改进方向。譬如，朴素线性注意力 使用类似Hebbian 的更新，已被证明** 容量有限**。后续 Hopfield 工作通过** 高阶多项式与指数核提升记忆容量，这也与 多项式核的线性注意力相关。另一方面，Delta Rule被证明具有 更好的记忆容量**。在** 固定大小的循环状态下，Delta Rule能在“ 召回‑记忆**”权衡上取得** 更优前沿**，并已用于增强现实世界的** 检索任务；它在多个领域也优于线性 Transformer 的 加性规则**。尽管如此，Irie 等指出 delta 更新在** 表达力**上存在理论局限。

普通的Linear RNN中，维护一个矩阵态 $S$ ：

S \leftarrow S + v k^{⊤}, o = S q,

如果两个 $k$ 不正交，会出现碰撞的情况：

o = 想要 v_{i} ⟨ k_{i}, q ⟩ + j \neq = i \sum v_{j} ⟨ k_{j}, q ⟩_{噪声} .

Delta Rule做一次SGD，得到：

S \leftarrow S - β (S k - v) k^{⊤},

能够收敛到最小二乘解：

S^{⋆} = ar g S min i \sum ∥ S k_{i} - v_{i} ∥^{2} = V K^{⊤} (K K^{⊤})^{- 1} (K K^{⊤} 可逆时),

而原版softmax注意力：

A = softmax (\frac{Q K ^{⊤}}{d _{k}}), O = A V .

直接显示保留了整个 $K, V$ 作为记忆，记忆能力非常强但 $n^{2}$ 开销。

为增强 DeltaNet 的递归能力，提出了 Recurrent DeltaNet 、Modern Self‑Referential Weight Matrix 、mesa‑layer 等，并显示更优。但这些模型超出了线性 RNN 范畴，** 无法跨序列并行，提示存在 并行性与表达力的根本权衡**。如何在** 不牺牲并行性的前提下进一步增强 DeltaNet 仍是开放问题；TTT 采用“ 跨块非线性 + 块内线性**”的混合策略，或许能提供折中路径。最后，Delta Rule与经由** 梯度下降的元/在线学习密切相关，近期如 ** Longhorn、** TTT予以重访； Titans进一步加入动量与权重衰减**。

7. Conclusion

我们给出了一个沿序列长度维度 并行化 DeltaNet 训练的算法，在现代硬件上相较既有实现取得了** 显著加速**。这使得将 DeltaNet 扩展到** 中等规模**语言建模成为可能；在该设定下，我们发现其相较近期的线性递归基线表现良好。

对于一个长度为 $C$ 的块内，定义 $K [t] \in R^{C \times d}, V [t]$ 同理，定义：

T [t] = (I + tril (diag (β [t]) K [t] K [t]^{⊤}, - 1))^{- 1} diag (β [t]) W_{[t]} U_{[t]} = T_{[t]} K_{[t]} = T_{[t]} V_{[t]}

那么就有：

W_{[t]} [r, :] = β_{[t]}^{r} K_{[t]} [r, :] - β_{[t]}^{r} i = 1 \sum r - 1 W_{[t]} [i, :] (K_{[t]} [i, :] K_{[t]} [r, :]^{⊤})

定义：

B_{[t]} = diag (β_{[t]}) L_{[t]} = tril (B_{[t]} K_{[t]} K_{[t]}^{⊤}, - 1)

则：

W_{[t]} + L_{[t]} W_{[t]} = B_{[t]} K_{[t]}

因此：

W_{[t]} = (I + L_{[t]})^{- 1} B_{[t]} K_{[t]} = T_{[t]} K_{[t]} T_{[t]} = (I + L_{[t]})^{- 1} B_{[t]}

另一个也同理。

U [t] = T [t] V [t], W [t] = T [t] K [t]

等价于一次把 $u_{r} = β_{r} (v_{r} - \sum_{i < r} u_{i} (k_{i}^{⊤} k_{r}))$ 中所有的 $u_{r}, w_{r}$ 递推，一次性通过单位下三角阵-对角缩放求出来。

将逐元素递推写成一次下三角线性方程的求解。 ↩
所以S6就改了。 ↩

Parallelizing Linear Transformers with the Delta Rule over Sequence Length