摘要： 随着智能移动设备的日益普及和基于深度学习模型的巨大计算成本，迫切需要高效且准确的设备端推理方案。我们提出了一种量化方案，允许仅使用整数运算进行推理，这种方案可以比在常见的仅支持整数运算的硬件上实现的浮点推理更加高效。我们还共同设计了一种训练程序，以保持量化后的端到端模型准确性。因此，所提出的量化方案改善了准确性与设备端延迟之间的权衡。即使在以运行时效率著称的MobileNets模型家族上，改进也是显著的，并且已在流行的CPU上展示了ImageNet分类和COCO检测的结果。

1. Intro

current quantization approaches are lacking in two respects when it comes to trading off latency with accuracy: First, prior approaches have not been evaluated on a reasonable baseline architecture. Second, many quantization approaches do not deliver verifiable efficiency improvements on real hardware.

文章认为先前的模型量化工作都存在两方面的问题，首先是量化的模型选择的一般都是AlexNet或者VGG这种”over-parameterized”的模型，它们为了提高精度实际上引入了过多的参数。对于这种模型，删除很多参数并且保留大部分精度是很容易的，这样量化方法声称的自己的压缩率实际上就没那么有意义。另一方面是大部分工作都只在理论上做inference performance的推断，还没有实际结合到设备上、利用芯片中有的部分做实际的inference。

Contributions:

We provide a quantization scheme that quantizes both weights and activations as 8-bit integers, and just a few parameters as 32-bit integers.
We provide a quantized inference framework that is efficiently implementable on integer-arithmetic-only hardware such as the Qualcomm Hexagon and we describe an efficient, accurate implementation on ARM NEON.
We provide a quantized training framework co-designed with our quantized inference to minimize the loss of accuracy from quantization on real models.
We apply our frameworks to efficient classification and detection systems based on MobileNets and provide benchmark results on popular ARM CPUs that show significant improvements in the latency-vs-accuracy tradeoffs for state-of-the-art MobileNet architectures, demonstrated in ImageNet classification, COCO object detection, and other tasks.

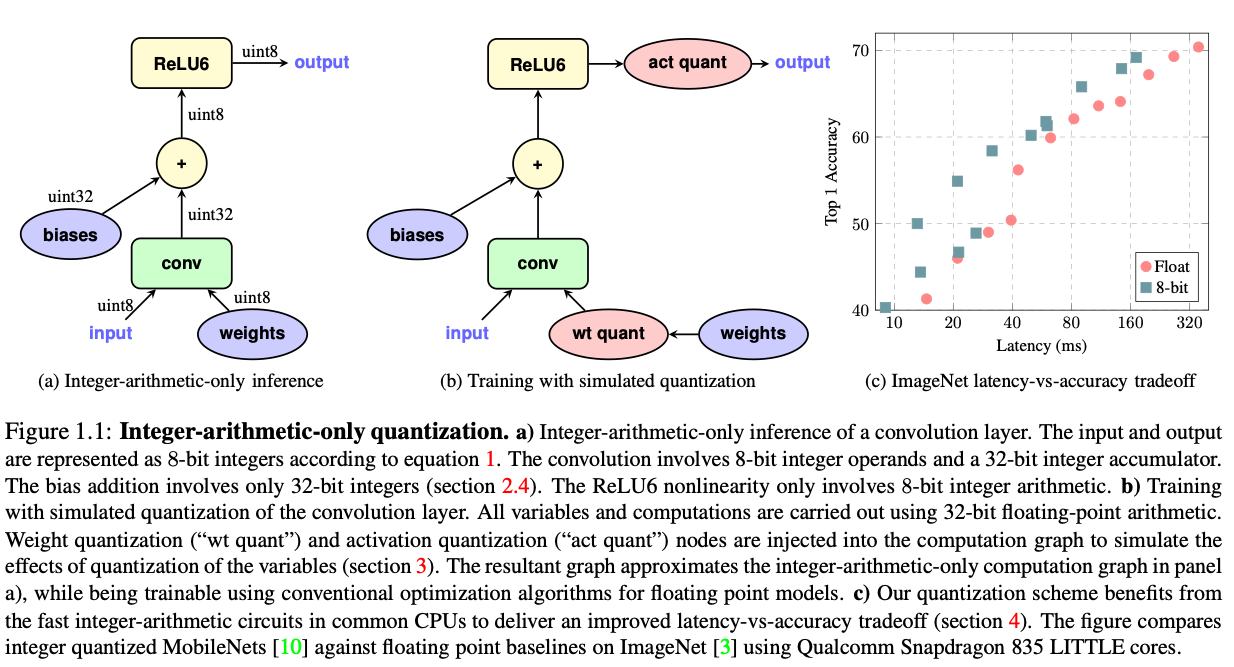
2. Quantized Inference

2.1. Quantization scheme

基础：

r = S (q - Z) (1)

$r$ 真值， $S$ 和 $Z$ 是量化参数， $q$ 是量化后的值。

2.2. Integer-arithmetic-only matrix multiplication

formula:

Consider the multiplication of two square $N \times N$ matrices of real numbers, $r_{1}$ and $r_{2}$ , with their product represented by $r_{3} = r_{1} r_{2}$ . We denote the entries of each of these matrices $r_{α} (α = 1, 2 or 3)$ as $r_{α}^{(i, j)}$ for $1 \leq i, j \leq N$ , and the quantization parameters with which they are quantized as $(S_{α}, Z_{α})$ . We denote the quantized entries by $q_{α}^{(i, j)}$ .

(1)写为：

r_{α}^{(i, j)} = S_{α} (q_{α}^{(i, j)} - Z_{α}) (2)

所以矩阵乘可以写为：

S_{3} (q_{3}^{(i, k)} - Z_{3}) = j = 1 \sum N S_{1} (q_{1}^{(i, j)} - Z_{1}) S_{2} (q_{2}^{(j, k)} - Z_{2}) (3)

把系数化简可以写作

q_{3}^{(i, k)} = Z_{3} + M j = 1 \sum N (q_{1}^{(i, j)} - Z_{1}) (q_{2}^{(j, k)} - Z_{2}) (4)

其中

M := \frac{S _{1} S _{2}}{S _{3}} (5)

(4)式里只有 $M$ 一个数不是整数，并且 $M$ 实际上是在量化过程中得到的，总是可以通过

M = 2^{- n} M_{0} (6)

转换 $M_{0} \in [0.5, 1) ， n$ 是非负整数。这样关于M的计算可以用定点乘法和移位实现。

2.3. Efficient handling of zero-points

为了对(4)式进行优化，避免进行 $2 N^{3}$ 次减法，可以把该式展开改写为：

q_{3}^{(i, k)} = Z_{3} + M (N Z_{1} Z_{2} - Z_{1} a_{2}^{(k)} - Z_{2} a_{1}^{(i)} + j = 1 \sum N q_{1}^{(i, j)} q_{2}^{(j, k)}) (7)

其中

a_{2}^{(k)} := j = 1 \sum N q_{2}^{(j, k)}, a_{1}^{(i)} := j = 1 \sum N q_{1}^{(i, j)} (8)

这样减少了减法操作，同时计算 $a_{1}, a_{2}$ 都是 $O (N^{2})$ 的，但是计算 $\sum_{j = 1}^{N} q_{1}^{(i, j)} q_{2}^{(i, j)}$ 是 $O (N^{3})$ 的，所以时间开销上还是更加关注后面这一项。

2.4. Implementation of a typical fused layer

观察Fig1，注意到还需要添加bias， $S_{bia s}$ 会是一个int32的数据，定义：

S_{bia s} = S_{1} S_{2}, Z_{bia s} = 0 (9)

先加bias再量化而不是先量化再加bias，是因为量化过程中引入的误差一般都是有偏的，这个有偏的误差可以通过修改bias来抵消一部分，bias的精度相对高的话对这个误差的调整精度也更高，就可以提升最后的accuracy。

With the final value of the int32 accumulator, there remain three things left to do: scale down to the final scale used by the 8-bit output activations, cast down to uint8 and apply the activation function to yield the final 8-bit output activation.

down-scaling: 乘M(7)。这篇文章没有把RELU融合进来，并且发现量化训练的过程中规模会学会利用整个uint8的范围，相当于让激活函数事实上不起作用。

3. Training with simulated quantization

这篇文章之前的工作主要是浮点训练完成后量化（QAT），文章发现QAT在小规模模型上表现比较差，因为：

1. 不同的channel之间weight的范围差异很大，但是前面的量化方法都会把它们量化到同一个范围里面，这样weight范围小的channel就会产生大量的误差
2. 一个channel中的weight存在异常值就会影响整个模型的量化效果（跟1实际上讲的是同一个东西）

为了解决这个问题，提出一种在前向传播的过程中模拟量化效应的方法。反向传播的时候还是用浮点训练，前向传播的过程用一种模拟量化的方法：

1. weight先量化再计算（卷积），如果包含batch norm，还要把batch norm融合到量化的过程中
2. 推理的时候按照inference中的规则对activation做量化，比如做完了卷积之后

每层中的量化由下面的方法执行：

clamp (r; a, b) = min (max (x, a), b) s (a, b, n) := \frac{b - a}{n - 1} q (r; a, b, n) := [\frac{clamp ( r ; a , b ) - a}{s ( a , b , n )}] s (a, b, n) + a (10)

$[a; b]$ 是量化范围， $n$ 是量化阶级数量。实验中 $n$ 恒定取256.

3.1. Leaning quantization ranges

对于weight和activation的量化范围的处理方法有不同。

对于权重，基本就是直接认为 $a := min w, b := max w$ ，然后调整到 $[- 127, 127]$ 之间，并且保证永远不取-128。
对于activation，范围取决于输入，通过维护训练期间看到的min or max的指数移动平均EMA来估计

3.2. Batch normalization folding

训练的时候把batchnorm拆成单独的，推理的时候把batchnorm吸收到对应的卷积或者全连接操作中。但是这种吸收操作本身可能也会带来量化损失，用如下式子估计：

w_{f o l d} = \frac{γ w}{EM A ( σ _{B}^{2} ) + ϵ}

$γ$ 是batchnorm的缩放参数， $EM A (σ_{B}^{2})$ 是batch之间输出结果的方差的移动平均， $ϵ$ 用来防止除0的小量。

4. Experiments

在ResNet，Inception v3两个大体量的模型上做了测试，然后在小体量的MobileNets上做测试，两个项目都有压缩率和精度的提升

消融实验的结论：

weights are more sensitive to reduced quantization bit depth than activations, 2) 8 and 7-bit quantized models perform similarly to floating point models, and 3) when the total bit-depths are equal, it is better to keep weight and activation bit depths the same.

Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference