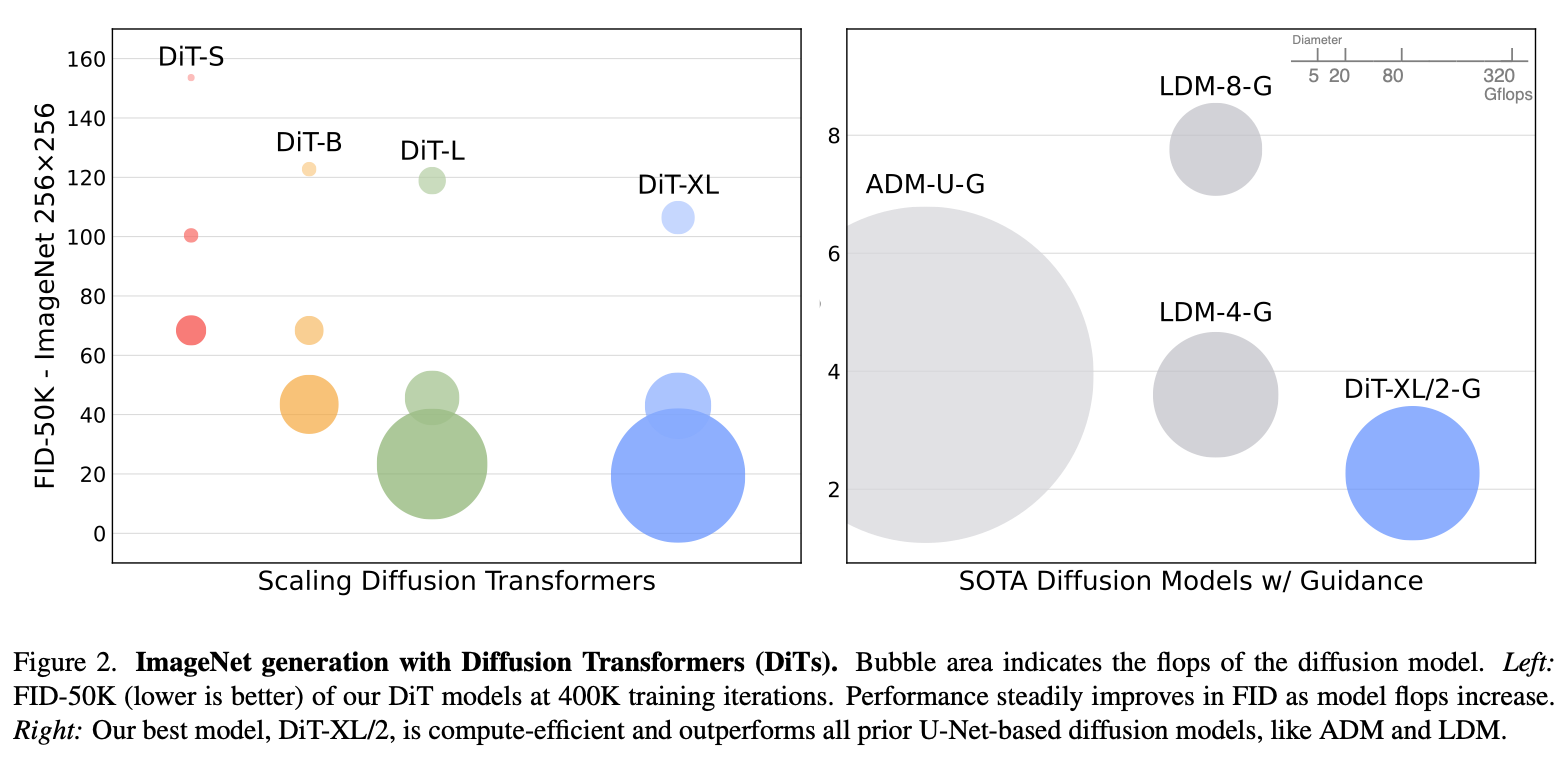
摘要： 我们探索了一类基于 Transformer 架构的新型扩散模型。我们在图像的潜空间（latent space）上训练潜扩散模型（latent diffusion models），并将常用的 U-Net 骨干替换为作用于潜变量补丁（patch）的 Transformer。我们从前向传播的复杂度（用 Gflops 度量）角度分析了我们的 Diffusion Transformer（DiT）的可扩展性。结果表明，具有更高 Gflops 的 DiT（通过增加 Transformer 的深度/宽度或增加输入 token 的数量）能够稳定地获得更低的 FID 分数。除了良好的可扩展性之外，我们规模最大的 DiT-XL/2 模型在类条件的 ImageNet 512×512 和 256×256 基准上都优于之前的扩散模型，其中在 256×256 任务上达到了最新的最优 FID=2.27。

1. Intro

之前的Diffusion Model一般用U-Net做Backbone，是因为在GAN之类的网络里面它已经取得了一些成功。本文使用在CV领域近期火热的Transformer结构替换U-Net，称之为Diffusion Transformer（DiT）。

在本文中，我们重点研究了 DiT 在“网络复杂度与采样质量”之间的关系。我们发现，通过在 Latent Diffusion Models（LDMs）的框架中构建与测试 DiT 设计空间（用 Transformer 替换 U-Net 骨干），DiT 能够很好地取代 U-Net。此外，我们还发现 DiT 在扩散模型中具有良好的可扩展性：网络复杂度（用 Gflops 度量）与样本质量（用 FID 度量）之间存在显著相关性。只需简单地扩大 DiT 规模，并在高容量（118.6 Gflops）骨干下训练一个 LDM，我们就能在 ImageNet 256×256 类条件生成上实现 2.27 的最新最佳 FID。

Transformers
DDPMs
Architecture complexity：图像生成中不能仅仅看模型参数，比如更大的分辨率会影响图片质量，看模型参数不能完全体现计算复杂度，一般是看GFLOPs。

3. Diffusion Transformers

3.1. Preliminaries

Diffusion formulation

回顾一下DDPMs，高斯扩散模型假设一个前向的加噪过程，将 $x_0$ 真实数据慢慢加噪得到 $x_t$ ：

q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{\overline{\alpha}_t}x_0, (1-\overline{\alpha}_t)\textbf{I}),

其中 $\overline{\alpha}_t$ 是若干超参数。通过参数重整化可以写作：

x_t=\sqrt{\overline{\alpha}_t}x_0+\sqrt{1-\overline{\alpha}_t}\epsilon_t, \quad \epsilon_t\in \mathcal{N}(\textbf{0},\textbf{I})

扩散模型就是为了学习反向的去噪过程：

p_\theta(x_{t-1}|x_t)=\mathcal{N}(\mu_\theta(x_t), \sum_\theta(x_t)),

神经网络预测的就是这个正态分布的均值和方差。模型通过最大对数似然的变分下界训练，写作：

\mathcal{L}(\theta)=-p(x_0|x_1)+\sum_t\mathcal{D}_{\text{KL}}(q^*(x_{t-1}|x_t, x_0)||p_\theta(x_{t-1}|x_t))

因为知道 $q^*$ 和 $p_\theta$ 都是正态分布分布，可以直接算它们的KL散度训练。如果将 $\mu_\theta$ 重参数化为一个噪声预测网络 $\epsilon_\theta$ ，又可以通过最小化噪声预测的MSE来训练：

\mathcal{L}_{\text{simple}}(\theta)=||\epsilon_\theta(x_t)-\epsilon_t||^2_2

但这么训没学到 $\sum_\theta$ 那一项，所以一般是先用上面这个式子学均值，然后用完整的KL散度学方差。训练完成之后，从一个随机的正态分布噪声初始化 $x_{t_{\text{max}}}$ ，然后一步一步还原。

Classifier-free guidance

假设有prompt之类的标签需要条件训练，则有

p_\theta(x_{t-1}|x_t, c)

Classifier-free guidance的思路是在采样的时候放大条件对结果的影响，从而获得更好的结果。

根据贝叶斯公式， $\log{p(c|x)}\propto \log{p(x|c)}-\log{p(x)}$ ，假设扩散模型的输出是一个分数函数，那可以通过：

\hat{\epsilon}_\theta(x_t, c)=\epsilon_\theta(x_t, \varnothing)+s\cdot [\epsilon_\theta(x_t,c)-\epsilon_\theta(x_t,\varnothing)]

放大条件的影响， $s\ge1$ 控制放大尺度， $\varnothing$ 表示在训练阶段通过随机丢弃条件学到的空embedding。

Latent diffusion models

直接生成超大规模的图像计算量太大了，LDMs一般采用两阶段的方法：

先训练一个Encoder，将图像压缩到更小的表示；
在Latent Space上训练Diffusion模型，然后用Decoder将模型输出还原到原来的图像尺寸上。

本文采用类似的模式。

3.2. Diffusion Transformer Design Space

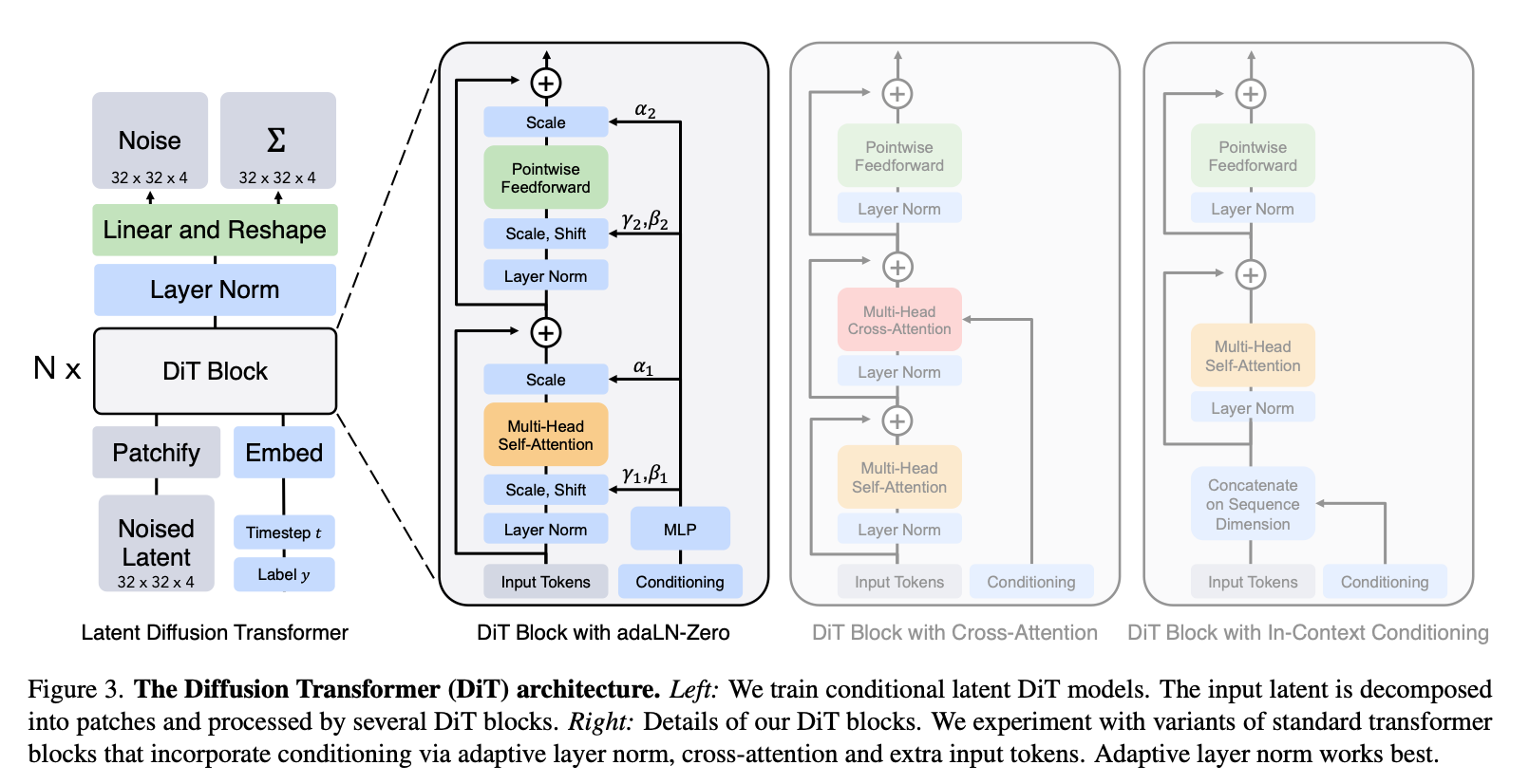
整体思路沿袭ViT的思路。

3.2.1. Patchify

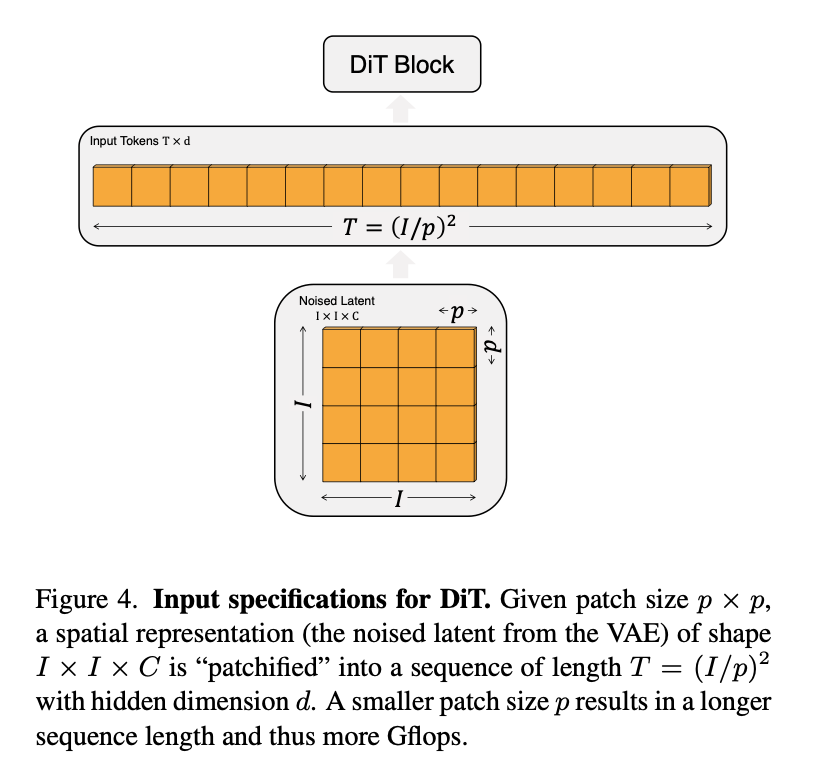
拆分成多个patch然后过一个linear层，映射成embedded input tokens。patch大小几乎不影响模型的参数量，但是显著影响模型的计算量：如果 $p$ 减半，input sequence长度 $T$ 扩大四倍。文章考察 $p=2, 4, 8$ 三种情况。

3.2.2. DiT block design

网络中要注入 $t$ ，引入 $c$ 标签等各种信息，调整这些方法形成了架构图里面的各种不同的Attention：

In-context conditioning：直接把 $t$ 和 $c$ 的embedding拼到序列的末尾，块中不做区别，推理完了再把最后这段去掉；几乎不增加额外计算量；
Cross-attention conditioning： $t$ 和 $c$ 拼起来单独当作一个输入，在input seq做完一次self attention之后再和这个conditioning做一次cross attention；增加约15%的GFLOPs；
Adaptive layer norm conditioning：LayerNorm的参数 $\gamma$ 和 $\beta$ 是通过 $t$ 和 $c$ 的向量和中回归出来的，而不是训练的时候学出来的；不引入额外计算量；
adaLN-Zero Block：在adaLN的基础上再学一组 $\alpha$ ，每个残差链接之前都会先乘以 $\alpha$ ，这些参数最开始会被初始化成0，这样这个残差链接最开始相当于”不存在“，最开始等价于恒等映射，据说比较好训练；

3.2.3. Model size

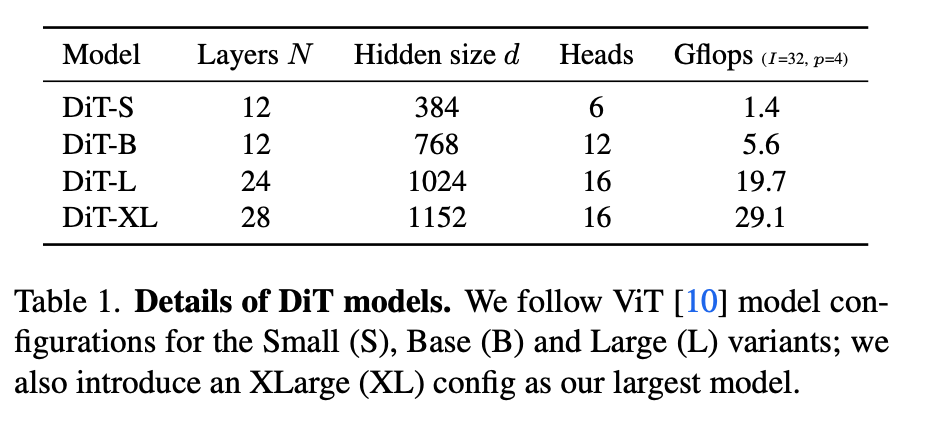
3.2.4. Transformer decoder

最终输出之前，首先做一次LayerNorm，然后通过一个Linear映射到 $p\times p\times2C$ 的tensor上，再把这个tensor折叠成 $p\times p\times C$ 的，得到最终的噪声和对角方差预测。

4. Experimental Setup

Training

ImageNet, 256256和512512训，最后一层Linear初始化成0（为什么？）之外其他用ViT的一般方法做初始化。

优化器方面，我们采用 AdamW ，学习率固定为 $1\times10^{−4}$ ，无学习率预热或衰减，weight decay 设为 0，batchsize为 256。与大多数 ViT 研究不同，即使不使用学习率 warmup 和额外正则化，我们仍能稳定训练各种规模的 DiT，且训练过程中未出现 Transformer 常见的 loss 崩溃现象。我们还遵循生成模型的惯例，使用指数滑动平均（EMA）进行参数动量更新，衰减系数为 0.9999。本文的所有结果都基于 EMA 参数。除以上变动外，其他训练超参数（如学习率、Adam $\beta_1, \beta_2$ 、weight decay 等）均与 ADM 保持一致。

Diffusion

使用Stable Diffusion的VAE，做八倍下采样。最多1000步。

Evaluation metrics

FIS。250步DDPM的FID-50K。

Compute

在TUP上训，最大的DiT-XL/2在TPU v3-256（256个TPU Core）上训练的时候大概5.7 iterations/second。

5. Experiments

DiT block design

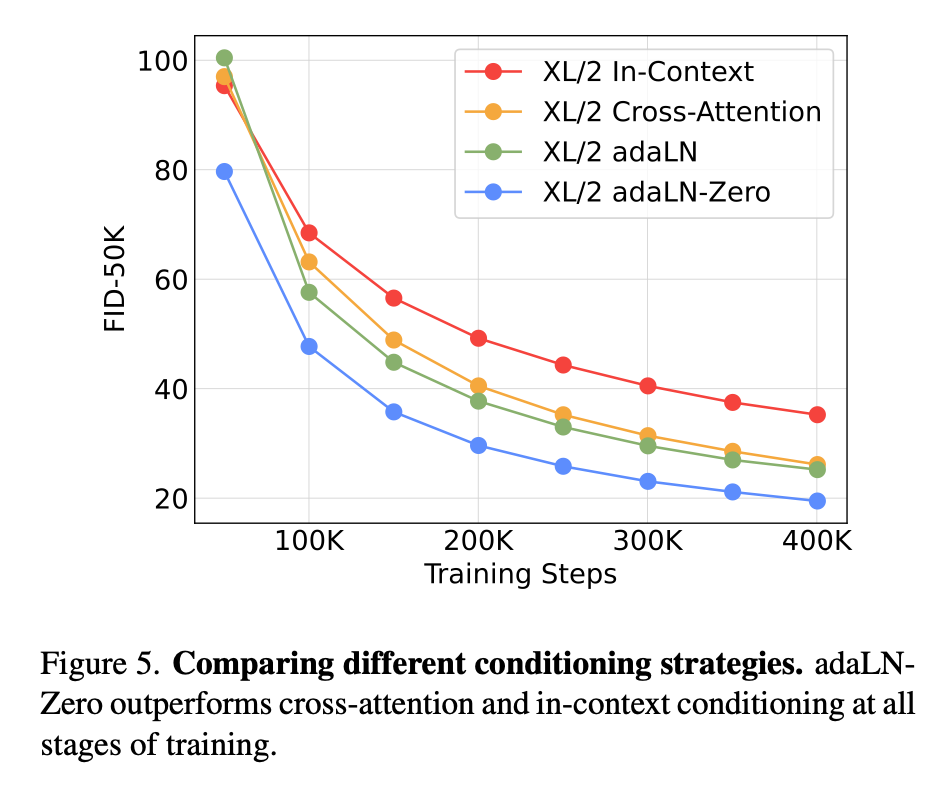
addLN-Zero好。

Scaling model size and patch size

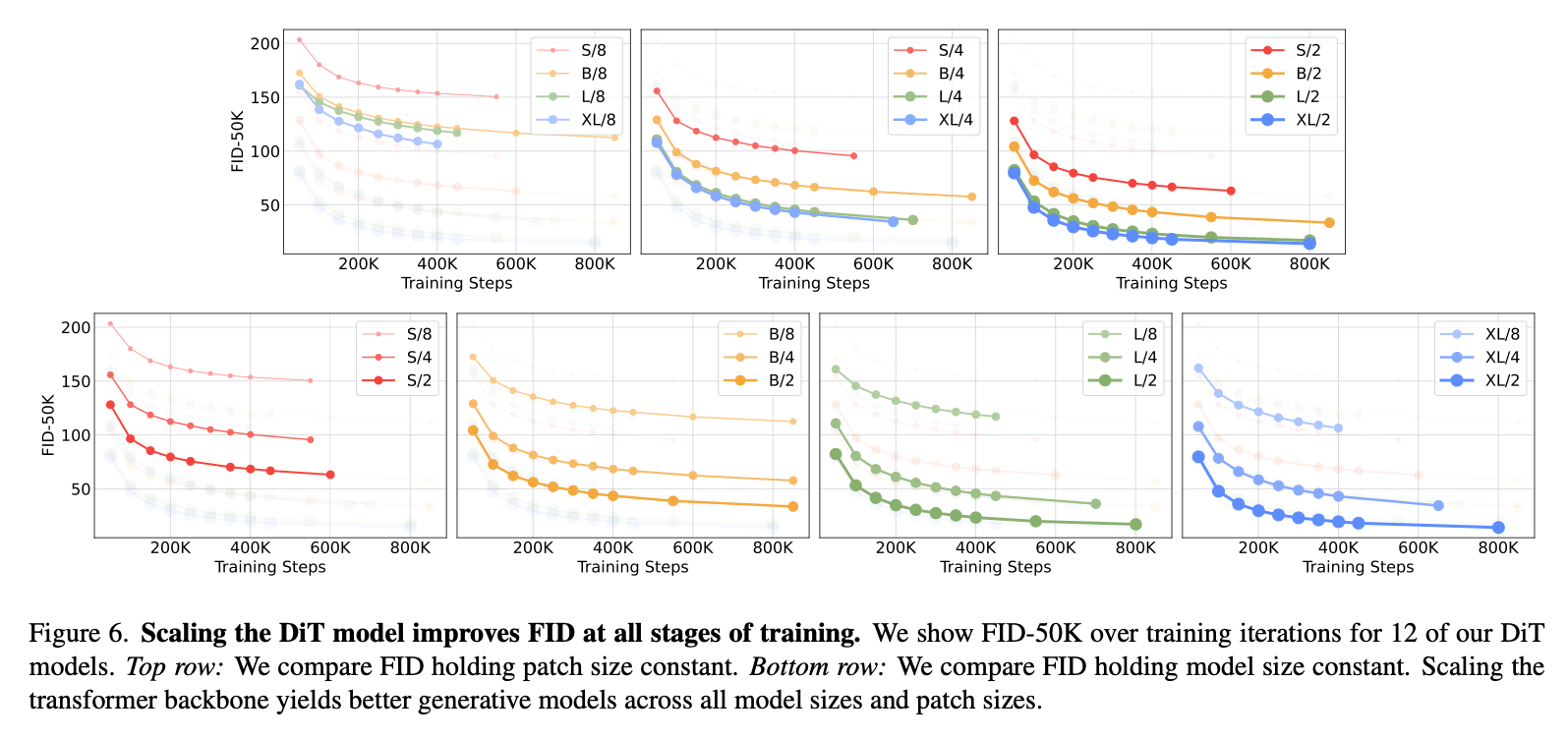
更大模型/更小patch效果更好。

DiT GFLOPs are critical to improving performance

Fig6，小patch = 大GFLOPs但参数不太变化，证明GFLOPs对Diffusion模型还是更好一些。

Larger DiT models are more compute efficient

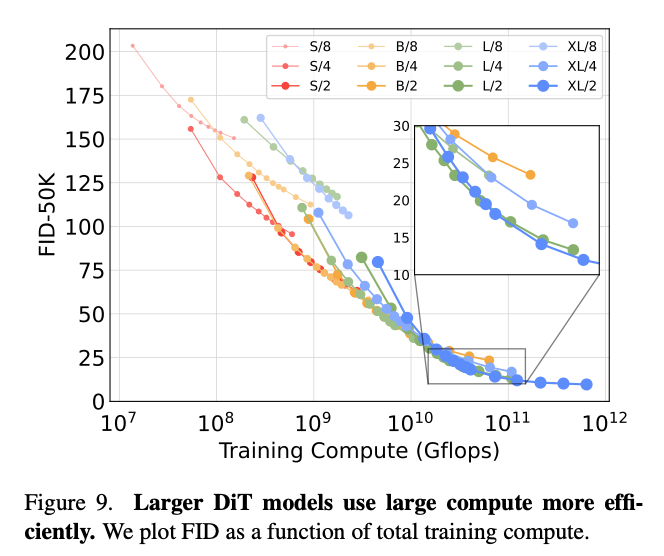
训练量 = GFLOPs * Batchsize * 训练步数 * 3，比较训练量和FID，可以发现小模型训很多步也追不上大模型在相同训练量下训少几步。

Visualizing scaling

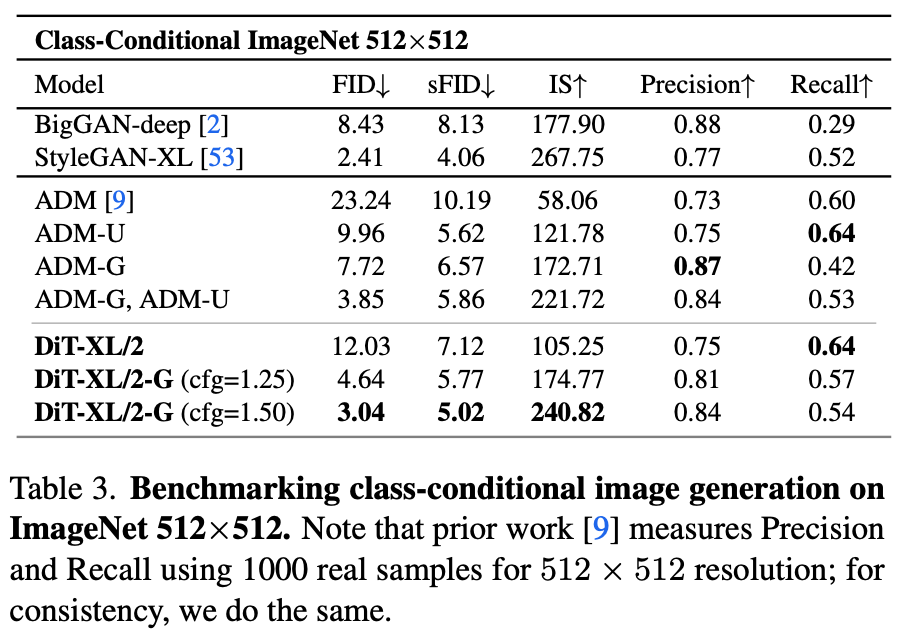
5.1. State-of-the-Art Diffusion Models

$256\times 256$ ImageNet.

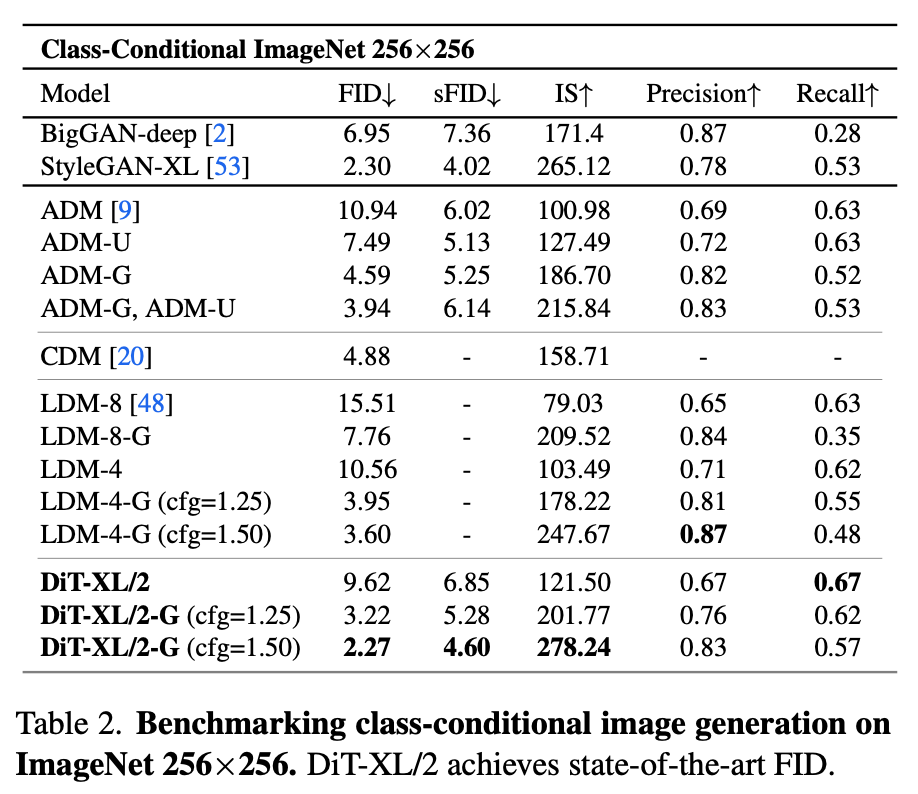
$512\times 512$ ImageNet.

5.2. Scaling Model vs. Sampling Compute

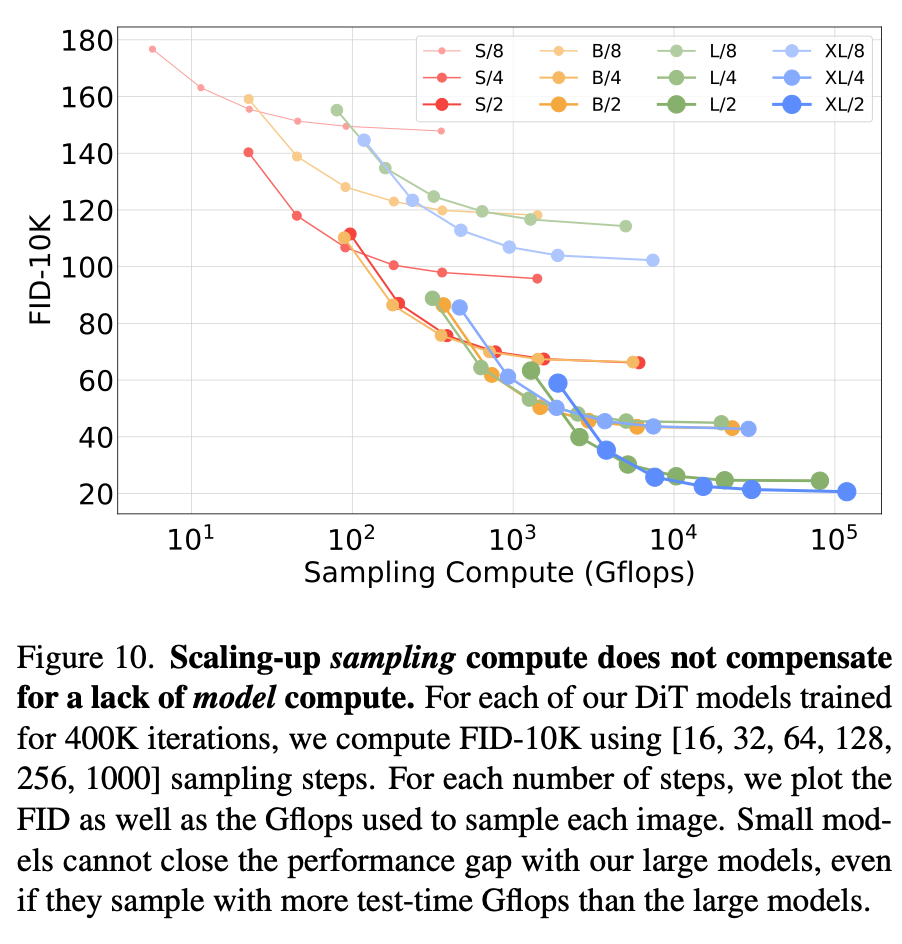
靠增加denoising的步数提高的计算量不能很好提高结果质量，小模型始终无法靠增加推理计算来弥补网络规模的不足。

6. Conclusion

我们在本文中提出了基于 Transformer 的扩散模型Diffusion Transformers (DiTs) ，表明扩散模型并不一定依赖 U-Net 架构，也能通过标准化的 Transformer 设计达到甚至超越最先进的图像生成性能。值得强调的是，DiT 继承了 Transformer 优秀的可扩展性：在大量实验中，我们反复验证了网络规模（Gflops）对生成效果具有决定性影响，并成功在 ImageNet 256×256 和 512×512 的类条件生成上超越了所有之前的扩散模型。面向未来的工作可以继续在更大规模和更长序列（更高分辨率）方向上扩展 DiT，也可把 DiT 作为可插拔的骨干迁移到诸如 DALL·E 2、Stable Diffusion 这类文本到图像模型中，让其充分利用 Transformer 在多模态场景中的优势。

DiT，在准备学DiT加速之前先读一读DiT做图片和视频生成的文章。这个里面的实验提了个很有意思的事情，模型的权重是一方面，假设在LLM里面做CoT之类的东西，但是要求每次回答一定要把Context Length跑慢，对复杂的问题一定要想的足够长，会不会也有文章里面说的这种，“小模型始终无法靠增加推理计算来弥补网络规模的不足”的结论？或者说，一个模型的实际推理能力其实更应该引入一些更公平的evaluation？LLM的大模型如果能学到，这次对话就是没有继续的上下文了，我要思考的足够久直到打满整个上下文，构建一个足够长的CoT是不是就刷点更高？

目前我使用LLM的方法其实也更倾向于一次把问题说清楚而不是多次交互，因为O1 Pro的上下文思考其实非常长，如果还包含了代码这样比较长的内容基本上两到三次对话之外的东西它久不太看的到了。如果在这种工作方式下，也许打满上下文的做法更好？做LLM Benchmark的时候是不是也是这样？

Scalable Diffusion Models with Transformers