摘要： 诸如 BERT 之类的语言模型预训练在多项 NLP 任务中都取得了显著成效。然而，人们尚不清楚“先预训练、再微调”这一范式为何能够在不同任务间提升性能与泛化能力。本文通过可视化 BERT 在特定数据集上的损失景观与优化轨迹来探究这一问题。我们的主要发现如下：1. 良好的初始点与宽阔的最优区域：预训练使模型在所有下游任务上一开始就处于较优位置，相较于从零开始训练，能够找到更宽阔的最优区域并带来更易于优化的过程。即便 BERT 参数量巨大，微调过程也表现出对过拟合的鲁棒性。2. 平坦宽阔的极小值与更好的泛化：可视化结果表明，微调后的 BERT 之所以更易泛化，是因为其损失景观平坦且宽阔，并且训练损失面与泛化误差面高度一致。3. 低层更加稳定、表示更可迁移：微调过程中，BERT 的低层（靠近输入的一侧）变化较小，说明这些层学习到的语言表示具有更强的可迁移性。

1. Intro

已有研究证明，预训练模型能够捕获语言的句法与语义信息。然而，从可训练性与泛化能力的角度看，预训练对下游任务有效的原因仍不明晰。本文以 BERT 为例，采用三种方式可视化微调过程中的损失景观和优化轨迹：

• 一维损失曲线  比较从零开始训练与微调 BERT 的差异；
• 二维损失面  相较一维曲线，提供更丰富的景观信息；
• 优化轨迹投影  将高维优化过程投射到所得二维损失面上，更直观地展示学习特性。

2. Background: BERT

介绍了一下BERT，问题的formulate。

给定输入文本的embedding$\{x_i\}^{|x|}_{i=1}$，可以拼接成$\text{H}^0=[x_1, ..., x_{|x|}]$。然后，经过$L$层的Transformer编码输入：$H^l=\text{Transformer\_block}_l(\text{H}^{l-1})=[h_1^L,...,h_{|x|}^L]$。

3. Methodology

为解释为何“微调预训练 BERT”比“从零开始训练”在下游任务上表现更佳，我们使用三种可视化手段：绘制 一维损失曲线 、二维损失面 ，并将优化轨迹 投射到损失面上。这些算法同样适用于随机初始化的模型，便于对比两种学习范式的差异。

3.1. One-dimensional Loss Curve

设$\theta_0$为初始化参数，对于fine-tune的过程而言，$\theta_0$是预训练的参数，对于train from scatch而言则是随机的初始化模型。训练结束之后，参数更新到$\theta_1$。

一维loss曲线表示了损失沿着优化方向的变化，定义为：

其中$\alpha$是标量，$\delta_1=\theta_1-\theta_0$为优化方向，$\mathcal{F}(\theta)$是损失函数。

3.2. Two-dimensional Loss Surface

类似前面的一维模式，还可以扩展到：

相似地，$\delta_1$是$\theta_1-\theta_0$的优化方向，而选取在另一个数据集上做finetune结束后的参数$\theta_2$，这样在高位空间之中$\delta_2=\theta_2-\theta_0$和$\delta_1$几乎是正交的。为了可视化，将$\delta_2$缩放到$\frac{||\delta_1||}{||\delta_2||}\delta_2$上。

3.3. Optimization Trajectory

记$\{\left(d_i^\alpha, d_i^\beta\right)\}^T_{i=1}$是一个优化轨迹，从上面的式子可以得到：

4. Experimental Setup

在MNLI, RTE, SST-2, MRPC四个数据集上做，用Adam优化器微调BERT-Large。

5. Pre-training Gets a Good Initial Point Across Downstream Tasks

在大多数情况下，将 BERT 作为初始化并进行微调，明显优于使用相同网络结构但随机初始化从零开始训练——在数据量较小时这一差距尤为显著。这些结果表明，语言模型的预训练目标为下游任务学习到了一组优良的初始参数。本节从三个角度考察把 BERT 当作起点能够带来的收益。

5.1. Pre-training Leads to Wider Optima

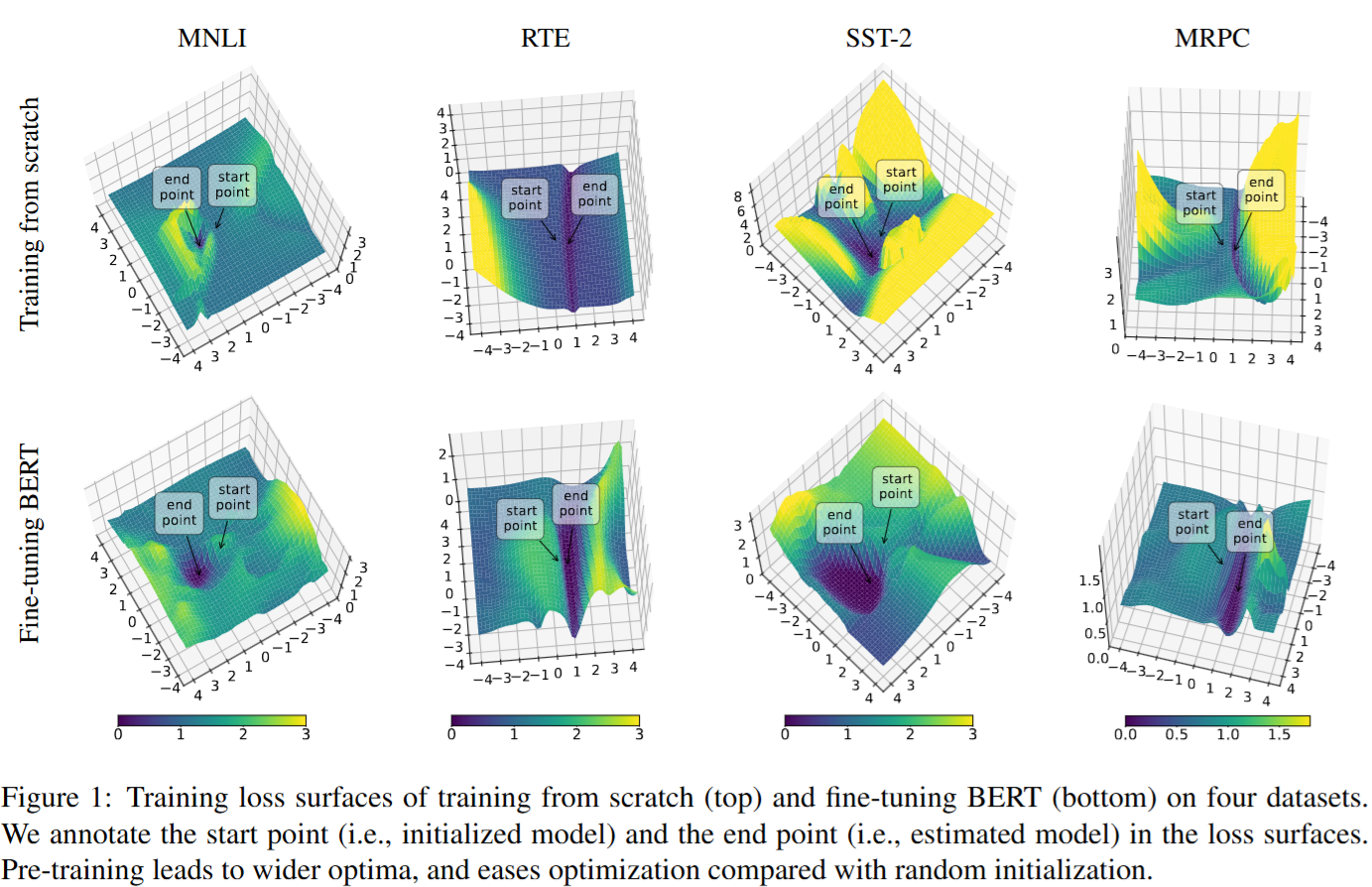
上面一排是train-from-scratch，下面一排是fine-tuning。总体来讲，做fine-tuning的Loss Landscape相比train-from-scratch得到的end point附近是相对平坦的，这意味着参数出现微小变化的时候，模型的性能不容易出现剧变。图还显示，从 Start 到 End 的微调路径相比随机初始化更加平滑：训练损失几乎单调下降，优化更容易、收敛更迅速；而随机初始化的路径更崎岖，需要更精细地调节优化器才能获得可接受的性能。

5.2. Pre-training Eases Optimization on Downstream Tasks

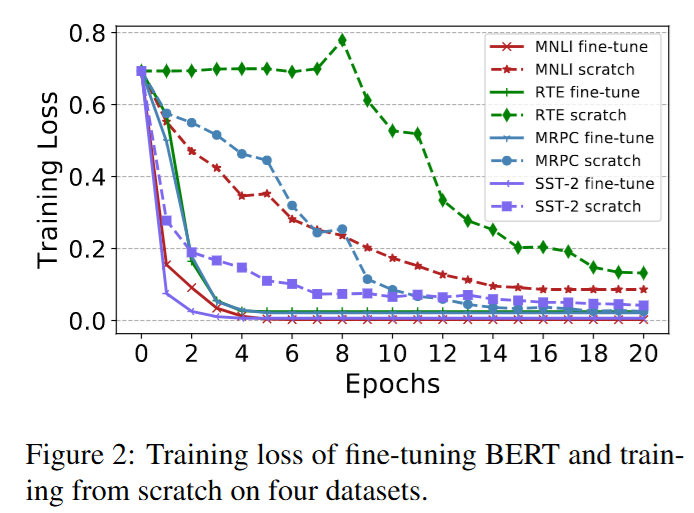
在上面四个任务中训练的Loss曲线如图，基本可以看到，train-from-scratch需要收敛的epoch更多，并且最终的loss的数值高于fine-tune。按照3.3中的方法绘制了优化轨迹：

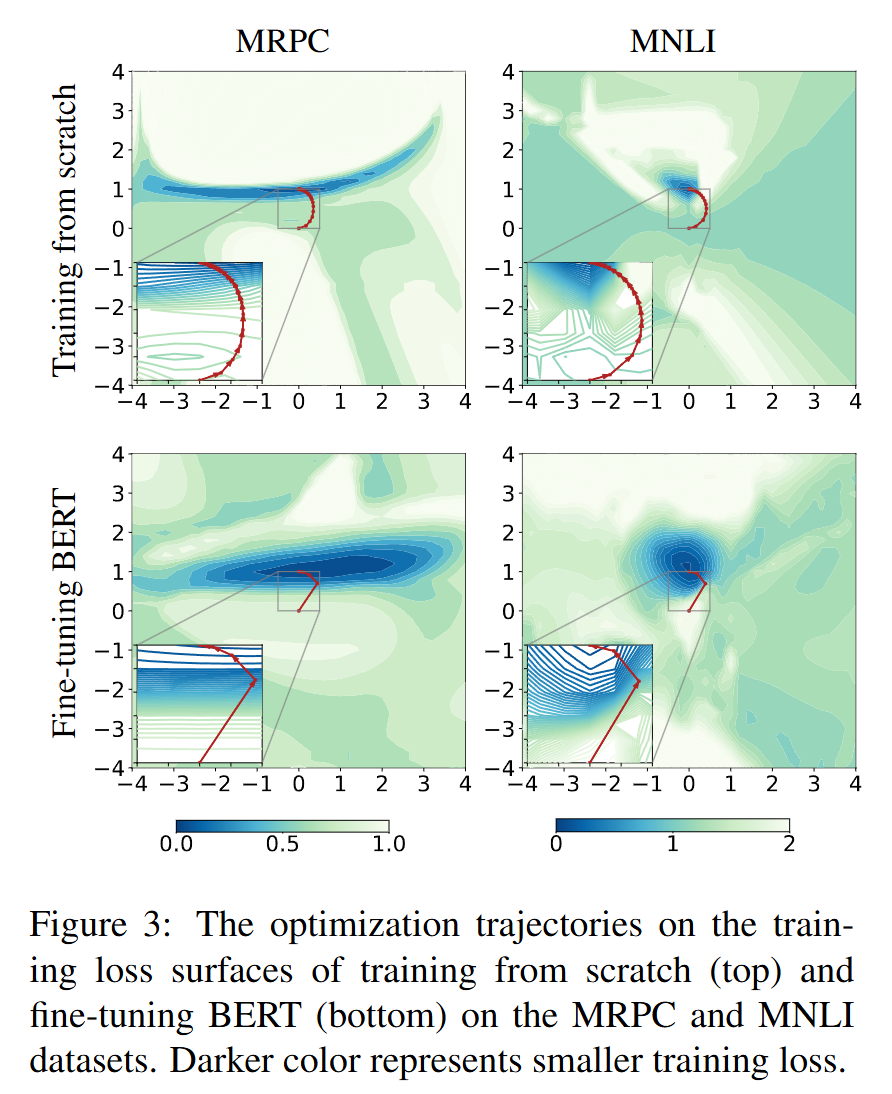
可以看到fine-tune的轨迹比train-from-scratch的轨迹更加“直接”，路径更”通畅“。

5.3. Pre-training-then-fine-tuning is Robust to Overfitting

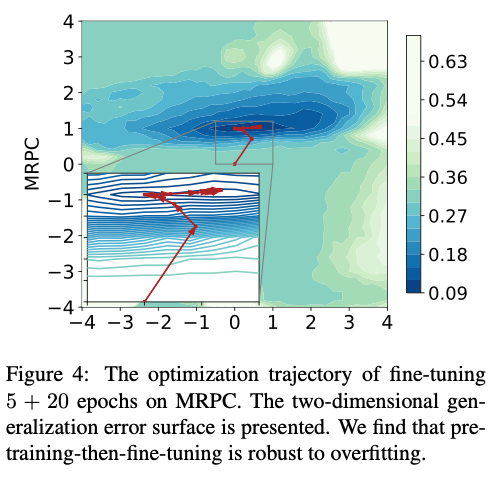
pretrain之后模型已经落在一个比较平坦宽阔的区域了，再微调也就是在这个区域内部移动，不容易跑到其他的非最优的位置去。

6. Pre-training Helps to Generalize Better

6.1. Wide and Flat Optima Lead to Better Generalization

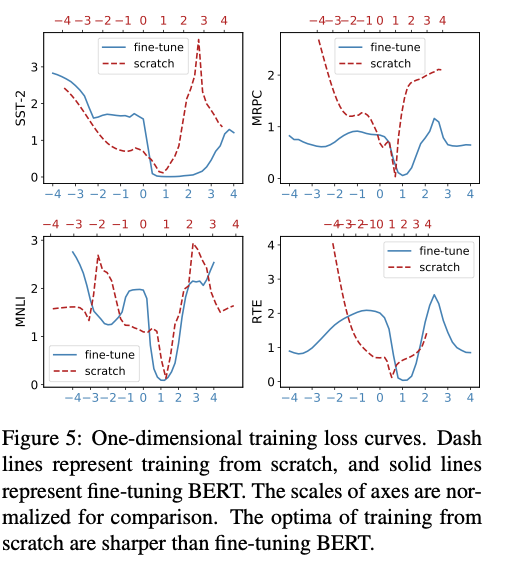
微调 BERT 的最优解更平坦，而随机初始化得到的更尖锐；因此，前者在看不见的数据上往往泛化更佳。

6.2. Consistency Between Training Loss Surface and Generalization Error Surface

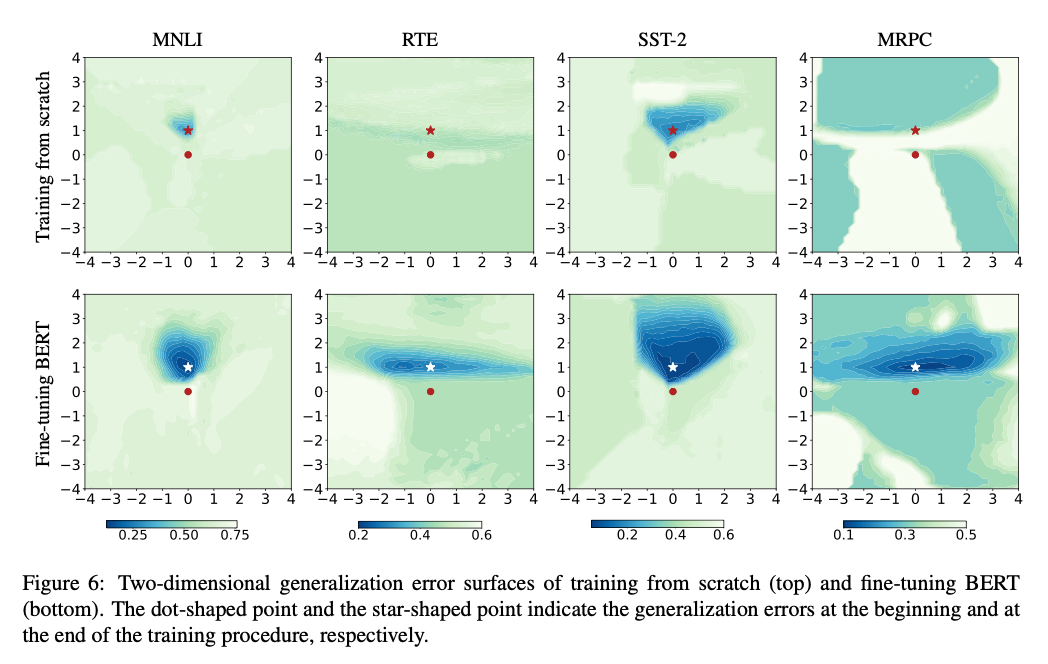
微调 BERT 的终点位于泛化误差较小且区域较宽的区域；这说明：

• 训练损失较小通常意味着泛化误差也较小 ；
• 当训练与泛化两种曲面相互平移时，宽而平坦的局部最优更加理想。

7. Lower Layers of BERT are More Ivariant and Trasnferable

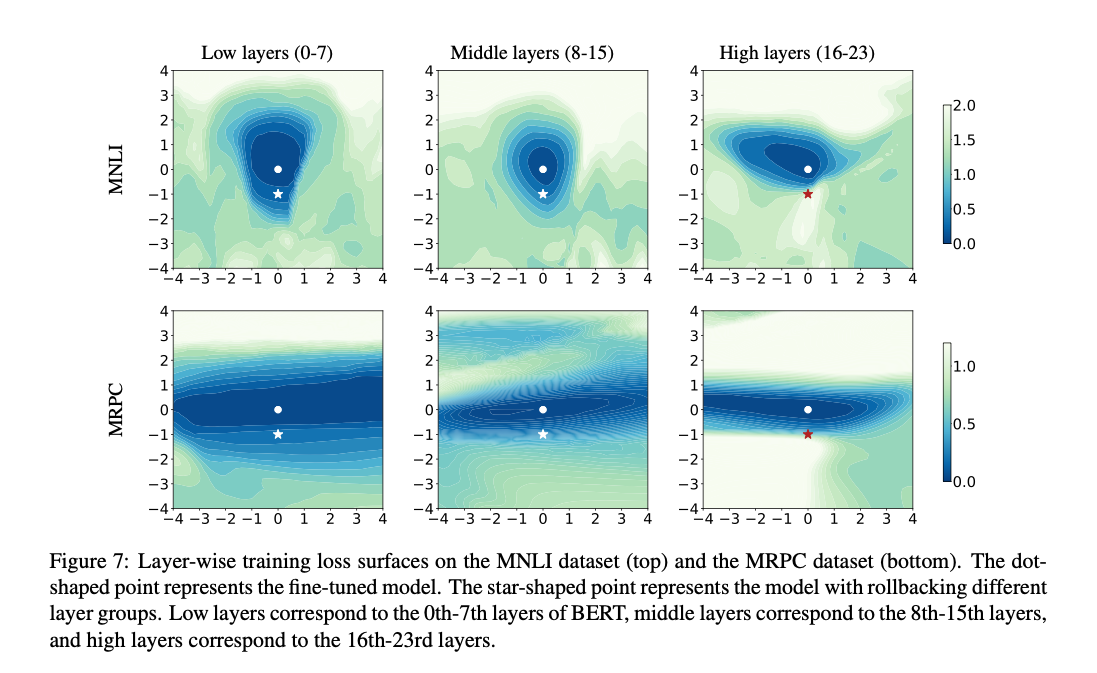
将24层的BERT-Large分为低（0-7）、中（8-15）、高（16-24）三组，将3.2中的$f(\alpha, \beta)$修改为：

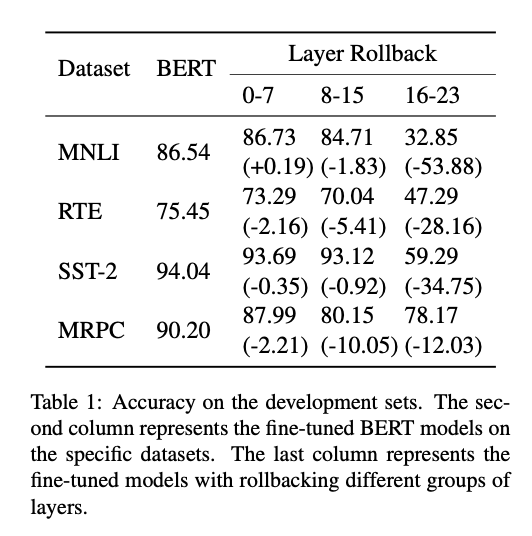
其中$G\in\{\text{低, 中, 高}\}$。可以看到更低的层分布的更加平坦。把低层或中层参数回滚到预训练状态（图中星形点）不会明显损害性能；而回滚高层则使损失急剧上升。这表明：下游任务的微调主要依赖高层的调整，而低层跨任务更为不变、可迁移。

8. Related Work

在计算机视觉领域，已有大量工作通过可视化损失函数来研究其几何形状与泛化性能的关系 (Goodfellow 和 Vinyals, 2015; Im 等, 2016; Li 等, 2018)。Hochreiter 和 Schmidhuber (1997) 将“平坦度”定义为极小值附近连通区域的大小；Keskar 等 (2016) 通过 Hessian 特征值刻画平坦度，指出小批量训练倾向于收敛到平坦极小值，从而具有更好的泛化；Li 等 (2018) 提出滤波归一化方法以消除参数规模影响，进一步证实极小值的尖锐程度与泛化能力高度相关。上述假设也被用于设计旨在找到更宽广极小值的优化算法。

本文从另一视角探索预训练的有效性：我们可视化了 BERT 微调过程中的损失景观与优化轨迹，直观地展示预训练带来的益处，更重要的是，损失几何部分解释了为何微调 BERT 比从头训练具有更好的泛化能力。

9. Conclusion

本文通过可视化 BERT 微调过程的损失景观与优化轨迹，发现与从头训练相比，预训练能带来更宽的极小值并简化优化 。同时，我们证明了“预训练-微调”范式在防止过拟合方面更为稳健，并展示了训练损失面与泛化误差面的形状一致性，从而解释了预训练为何提升泛化能力。此外，我们确认 BERT 低层在不同任务之间更加不变且可迁移。

所有实验与结论均基于 BERT 微调。未来值得探索多任务训练如何进一步改善微调及其对损失面的影响；同时，这些结果也激励我们开发能够收敛到更宽、更平坦极小值的微调算法，以期在未见数据上获得更好泛化性能。此外，将本文方法应用于其他预训练模型亦是有前景的研究方向。

最后画出来的图像稍微有点问题，自己造的数据不是很好，不过方法学到了。很有趣。